
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
О возможности построения упругого потенциала по результатам одноосного растяжения-сжатия.
Известен ряд работ, в которых авторы пытаются построить упругий потенциал по результатам испытаний резины в условиях одноосного растяжения – сжатия [65, 67, 68]. Цель этих работ понятна – как уже отмечалось, проводить эксперименты в сложном НДС достаточно утомительно. Возникает вопрос: а можно ли с определенной (пусть даже не очень маленькой) точностью гарантировать результаты в сложном НДС, опираясь на эксперименты растяжения-сжатия? Пусть имеется экспериментальная зависимость плотности энергии деформации от деформации при одноосном нагружении U(l1) для несжимаемого материала (l1l2l3 = 1), которая принадлежит поверхности упругого потенциала U*(l1, l2). Тогда
Построим упругий потенциал вида
где Q(l1,l2) - произвольная неотрицательная ограниченная функция, имеющая размерность плотности энергии, симметричная по аргументам и обращающаяся в ноль при равенстве аргументов единице. Очевидно, что потенциал (2.5.2) удовлетворяет условию (2.5.1), т.е. как и U*(l1l2), он превращается в функцию U(l1) в условиях одноосного нагружения. Следовательно, все потенциалы вида (2.5.2) при разных Q(l1,l2) будут одинаково хорошо совпадать с экспериментом в условиях одноосного нагружения, но во всех прочих деформированных состояниях могут отличаться друг от друга на сколь угодно большие конечные величины. Итак, по данным одноосного нагружения в самом общем случае невозможно сказать, как хорошо будут предсказаны свойства в сложном НДС. Каждый раз требуется экспериментальная проверка величины допускаемой погрешности. 2.6 Экспериментально-расчетный метод определения плотности энергии деформации в зависимости от инвариантов деформации
В настоящем разделе предлагается метод реализации однородного сложного НДС на стандартных разрывных машинах. В обзоре говорилось о том, что сложное НДС до настоящего времени воспроизводят на кустарном оборудовании, не обеспечивающем достаточную точность, как при задании условий испытаний, так и при получении результатов. Основные из этих методов следующие: двухосное растяжение образца типа «крест»; раздувание с одновременным растяжением резинового образца в виде трубы. Нами предложено и изготовлено приспособление, позволяющее использовать современное оборудование, такое, как разрывные машины типа Тензометр Т-10 (ф. Монсанто) и УТС – 10 (Германия).
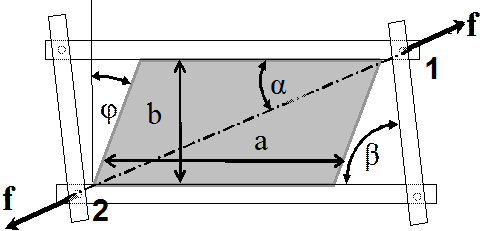
Принципиальная схема приспособления, которое представляет собой параллелограмм с жесткими сторонами и переменными углами, показана на рис. 2.6.1. Будем в дальнейшем называть его «рамка». Испытываемый образец представляет собой резиновую пластину с размерами 30х165х2 (мм). Закрепляя образец в рамке так, как указано на рисунке и прикладывая растягивающее усилие F к вершинам 1 и 2, получаем однородное деформирование резины, представляющее собой, как и прежде, суперпозицию чистого и простого сдвигов. Величина чистого сдвига определяется нормальной составляющей перемещения верхней стороны параллелограмма относительно нижней (b-bо), величина простого сдвига g - углом j. Рамка устроена таким образом, что боковые стороны являются сменными и имеют разные длины. Эти длины подобраны так, чтобы при деформировании получались разные соотношения деформаций чистого и простого сдвигов. Задача состоит в том, чтобы по перемещениям зажимов разрывной машины 1 и 2 рассчитать инварианты тензора деформации резинового образца. Эта задача может быть решена только в случае высокой степени однородности НДС резинового образца.
а)
б) Рис. 2.6.1 Схема приспособления для реализации сложного НДС, представляющего собой суперпозицию чистого и простого сдвига: а) до деформирования б) после деформирования Понятно, что проблема однородности, как и для случая чистого сдвига, связана с отношением b/a. Чем меньше это отношение, тем лучше. В нашем случае оно равно 0.18. Эта величина существенно меньше, чем аналогичные параметры в образцах – вилках при испытаниях в условиях простого сдвига и образцах – пробках при испытаниях на сжатие. В этих образцах также возникает проблема обеспечения однородности НДС. В процессе испытаний возникает еще одна проблема, которая требует обсуждения. Речь идет о смятии образца, или потере его устойчивости. На рис. 2.6.2 изображен такой случай. Это явление возникает тогда, когда главное напряжение по какой-либо из осей имеет отрицательное значение, т.е. это напряжение пытается сжать резиновый образец. Но образец тонкий и попытки его сжать приводят к тому, что он просто сминается, или теряет устойчивость. Поэтому для предотвращения указанного явления необходимо следить за тем, чтобы ни одна главная деформация не была бы меньше значения, соответствующего нулевому значению напряжения по данной оси. Например, в случае одноосного нагружения главные напряжения по одной оси больше нуля, а по другим двум равны нулю. Как только мы захотим уменьшить размеры по тем осям, где главные напряжения были равны нулю и где образец тонкий, последние сразу станут отрицательными и образец потеряет устойчивость.
Приведем расчет главных деформаций резинового образца. Запишем значения его параметров в исходном (недеформированном) состоянии (рис. 2.6.1): j = 0 – угол, характеризующий величину простого сдвига, b = bo - исходное расстояние между местами закрепления в рамку резинового образца (высота образца резины), a = a0 - величина угла между направлением силы F и осью горизонтальной планки, b = b0 – величина острого угла рамки-параллелограмма, B - константа, неизменный параметр конструкции рамки, L – длина сменной боковой планки. При деформации, т.е. при увеличении расстояния l12 между точками 1 и 2, угол b увеличивается под действием растягивающей нагрузки F. Величина b растет от bo до bmax = L-B, затем уменьшается (при j > 90). Однако при j > 90 процесс деформирования может оказаться неустойчивым в смысле появления смятия.
Рис. 2.6.2 Вид рамки и смятие резинового образца.
Выведем формулы для степени удлинения в нормальном направлении (величины чистого сдвига) ln = b/b0 и для величины простого сдвига g = tgj. Для этого запишем некоторые соотношения, следующие из геометрии рамки. Используем теорему косинусов:
Запишем два разных выражения для угла a (первое – из (2.6.1)):
Найдем из (2.6.2) значение b:
Выразим теперь b через угол b:
Из (2.6.4) найдем sinb и sinb0, через которые выразим g:
Выражение для ln = b/b0 сразу следует из (2.6.3). После того, как найдены составляющие простого и чистого сдвигов g и ln, соответствующие данному расстоянию между зажимами разрывной машины l12, инварианты тензора деформации резины записываются с учетом направлений главных осей и величин главных удлинений. Воспользуемся теорией, изложенной в разделе 2.3, и отошлем читателя к формулам (2.3.11) и (2.3.17), где эта задача уже решена. Следующая задача - из зависимости растягивающего усилия F от расстояния между зажимами l12 определить константы упругого потенциала. Эту задачу можно решить двумя способами. Первый предполагает интегрированием экспериментальной зависимости F(l12) получение энергии деформации Uэкспер.(l12). Далее методом, описанном в разделе (2.3), рассчитываются инварианты тензора деформации и далее константы потенциала. Этот способ, несмотря на прозрачность, недостаточно точен. Дело в том, что дифференцирование экспериментальных зависимостей (а получить значения компонентов тензора напряжений из упругого потенциала можно только дифференцированием) вносит большие погрешности. Хотелось бы иметь способ для непосредственного расчета констант потенциала из зависимости F(l12). Но эта задача не такая простая, как для случая одноосного растяжения, когда отлично от нуля значение главного напряжения только по одной оси.
Рассмотрим исходное состояние, при котором под действием нагрузки F образец деформировался и его главные деформации и главные условные напряжения равны l1, l2, f1, f2. Приложим к рамке дополнительную бесконечно малую нагрузку DF. Расстояние между точками 1 и 2 увеличится на бесконечно малую величину Dl, главные деформации изменятся на Dl1 и Dl2. Запишем уравнение баланса энергии:
Здесь V - объем деформируемой части резинового образца. Используем то обстоятельство, что зависимости l1(l12) и l2(l12) определяются однозначно и зависят только от размеров образца и параметров рамки. Эти функции гладкие и во всех точках имеют непрерывные производные l1¢(l12) и l2¢(l12). Следовательно, можно записать
Подставив (2.6.7) в (2.6.6) и сократив на Dl, получим:
Завершающий шаг состоит в том, чтобы в выражении (2.6.8) выразить условные главные напряжения f1 и f2 через производные упругого потенциала. Этот раздел вынесен в Приложение 2.
|
||||||||||
|
Последнее изменение этой страницы: 2017-02-08; просмотров: 566; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.186.173 (0.019 с.) |
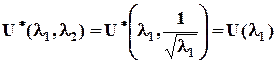 . (2.5.1)
. (2.5.1)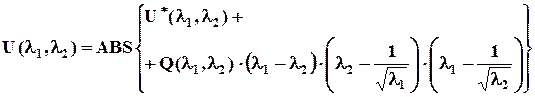 , (2.5.2)
, (2.5.2)

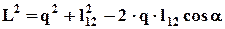 (2.6.1)
(2.6.1)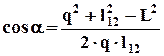 ,
,  (2.6.2)
(2.6.2) (2.6.3)
(2.6.3)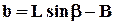

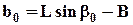 (2.6.4)
(2.6.4) (2.6.5)
(2.6.5)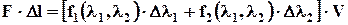 (2.6.6)
(2.6.6)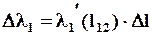
 (2.6.7)
(2.6.7)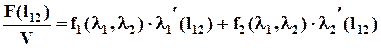 (2.6.8)
(2.6.8)


