
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Упругий потенциал несжимаемого тела для случая изотропности в деформированном состоянии
Как следует из литературного обзора, в настоящее время вопрос об оптимальных видах упругого потенциала нельзя считать закрытым как для ненаполненных, так и наполненных активными наполнителями (например, техническим углеродом) вулканизатов. Не вдаваясь в теоретические проблемы построения определяющих соотношений (уравнений состояния) на основе молекулярных представлений о строении полимерных цепей и сеток и о природе внутри - и межцепных взаимодействий (что выходит за рамки предлагаемого исследования), отметим, что современный уровень развития физики полимеров не позволяет получать уравнения состояния из первых принципов с учетом реального химического строения резины. Существующие модельные представления недостаточно детальны, чтобы на их основе строить потенциалы реальных вулканизатов. Практически все известные потенциалы (см. раздел 1.2) являются эмпирическими. Каждый из них предложен для описания поведения материалов определенного класса. Константы подбираются, как правило, с использованием метода наименьших квадратов на основе сравнения с экспериментом, проведенным в условиях одноосного растяжения – сжатия или простого сдвига. В ряде случаев сжатие заменяется двуосным однородным растяжением. Произвольное сложное НДС используется редко по причине сложностей его практической реализации. Феноменологические теории, построенные исключительно на принципах механики деформируемого твердого тела, крайне малочисленны. К ним в первую очередь следует отнести классические работы Муни [47] и Ривлина[31-33]. Муни построил свою теорию с использованием предположения о линейности зависимости условного напряжения от величины деформации простого сдвига. На этой основе получено уравнение (1.2.21). Ривлин предположил, что основное соотношение теории упругости для малых деформаций может быть применено и для конечных деформаций, однако выражения для гидростатического давления и тензора деформации изменятся. Это привело к уравнению (1.2.12). Подробно эти теории обсуждаются в главе 1. Возникает вопрос: можно ли построить упругий потенциал несжимаемого изотропного тела без привлечения дополнительных предположений о виде зависимости напряжения от деформации? Ответ на него может быть получен при более детальном анализе понятия изотропности.
Рассмотрим подробнее смысл этого понятия. Безусловно, в процессе одноосного растяжения резина становится анизотропным материалом, что проявляется, в частности, в зависимости величины двулучепреломления от приложенного напряжения (закон Брюстера) [41] или в каландровом эффекте [[253]]. Очевидно, что анизотропия в процессе растяжения вулканизата возникает не скачком, а плавно и в разной степени для разных свойств. В этой связи возможно предположение, что в некоторой окрестности вблизи недеформированного состояния величина анизотропии незначительна. Математически это означает, что закон деформирования по одной из главных осей не должен зависеть от величины деформации по другим осям и все следствия симметрии изотропного состояния распространяются и на деформированное состояние (повторим, что это утверждение выполняется тем точнее, чем меньшим деформациям подвергается материал). На вопрос о том, до каких величин деформаций это справедливо, может дать ответ в настоящее время только эксперимент. В подтверждение высказанного предположения можно привести результаты работы [66], где показано, что анизотропия упругих свойств ненаполненного аморфного вулканизата, сшитого в деформированном состоянии, проявляется не сразу, а только при некоторой конечной деформации (~30¸40%). Приведенные рассуждения можно использовать в качестве обоснования распространения понятия изотропности на деформированное состояние. Этими соображениями воспользуемся в предлагаемой теории. Известно, что любое сложное НДС может быть получено суперпозицией двух простых деформаций по разным главным осям. Рассмотрим процесс последовательного деформирования единичного кубического образца по оси X в l1 раз и по оси Y в l2 раз (рис. 2.1.1). После деформирования по оси Х зафиксируем возникшее при этом условное (отнесенное к исходному сечению) напряжение s1 = s1 (l1). Заметим, что напряжение s1 равно нагрузке f1, приложенной по оси Х, т.к. площадь грани Y-Z равна единице. Размеры образца при этом будут следующие:
Приложим к растянутому по оси Х образцу нагрузку f2=s2(l2)×
В результате размеры деформированного образца lx, ly, lz и степени одноосного растяжения l1, l2 будут связаны соотношениями
Из соотношений (2.1.2) легко получить обратные зависимости:
Покажем, что из соотношений (2.1.2) и (2.1.3) следует тождественность функций s1 (l) и s2 (l)× Из (2.1.2) следует, что при l1 = l2 выполняется соотношение ly = lх. Последнее равенство может быть выполнено только тогда, когда нагрузки f1 и f2, действующие по осям X и Y, равны друг другу, или, что то же самое,
Выражение для плотности энергии деформации U0 в зависимости от степени одноосного удлинения l выводится из следующих очевидных соображений (l0 - исходный размер испытываемого образца по оси приложения нагрузки; V0 – объем образца в недеформированном состоянии):
Запишем выражение для энергии деформирования образца U1 при его одноосном удлинении по оси Х на величину l1: U1 = С использованием (2.1.4) и (2.1.5) запишем выражение для энергии деформирования образца U2 по оси Y на величину l2: U2 = Прирастяжении по оси Y образец сократился по оси Х и совершил работу U3 (см. рис. 2.1.1):
Энергия, запасенная образцом в результате деформирования по двум осям, определяется соотношением: U = U1 + U2 - U3 (2.1.9) С использованием (2.1.4) - (2.1.8) имеем
Подчеркнем, что s(l) - закон одноосного деформирования из исходного состояния (условное напряжение). Изменим последовательность деформирования, т.е. сначала одноосно растянем образец по оси Х в l2 раз, затем так же одноосно по оси Y в l1 раз. По аналогии с предыдущими рассуждениями выражение для энергии деформирования в этом случае примет вид:
Очевидно, что U = U*, т.к. состояния в этих двух случаях, определяемые конечными размерами образца, тождественны. Проведем несложные преобразования:
Видно, что величины с индексами «1» и «2» стоят по разные стороны знака равенства. Используя это, а также соотношение
получим из (2.1.12) линейное дифференциальное уравнение
которое имеет строгое решение
Дифференцируя (2.1.14) последовательно два раза, получим выражения для напряжения s и модуля Е:
Подставив (2.1.15) в (2.1.10), получим выражение для плотности энергии деформации в произвольном однородном НДС:
Используя соотношения (2.1.2), получим
Выражение (2.1.18) получено строго с использованием только понятия изотропности, распространенного на деформированное состояние. Очевидно, что оно удовлетворяет требованию инвариантности. Однозначность решения свидетельствует о том, что все прочие потенциалы не удовлетворяют требованию изотропности деформирования, сформулированному выше.
Потенциал вида (2.1.18), называемый потенциалом Хазановича – Бартенева, достаточно давно обсуждается в литературе. Он является частным случаем общего выражения для зависимости плотности энергии деформации от инвариантов деформации в виде полинома
где J1 и J2 - любые независимые инварианты, а не только квадратичные, как это принято, в частности, в [5, 48]. Теоретическое обоснование выражения (2.1.18) с точки зрения простых представлений о сеточной структуре резины дано в [43], а в работах [44-46] описаны результаты эксперимента. Показано, что в сравнении с другими однопараметрическими выражениями потенциал (2.1.18) лучше описывает поведение ненаполненных резин не только при одноосном деформировании, но и во многих видах сложного НДС. Используя (2.1.2), (2.1.3) и (2.1.15), легко получить выражения для напряжений sx и s y через удлинения по главным осям lx и ly
В таблице 2.1.1 приведены экспериментальные данные Трилора [48, 54] по двуосному растяжению и расчетные данные по формулам (2.1.20). f1 и f2 – массы грузов в граммах, создающих натяжения по двум осям. Значение константы С в уравнении (2.1.10) определяли методом наименьших квадратов. Хорошо видно, что в области малых деформаций согласие теории и эксперимента практически идеальное. Некоторые отклонения наблюдаются при деформациях, приближающихся к 50%. В заключение следует еще раз подчеркнуть, что в прикладном смысле при расчетах резинотехнических изделий и шин не очень интересно поведение материала при больших деформациях, но весьма важную роль играет правильное описание НДС в диапазоне l=1.0 ¸ 1.5. В этой области идея о сохранении изотропности, лежащая в основе всего изложенного, представляется обоснованной для ненаполненных резин. Об этом свидетельствуют приведенные экспериментальные данные. Следующим шагом будет построение теории и получение экспериментальных данных для наполненных резин в произвольном сложном НДС. Мы увидим, что присутствие активного наполнителя существенно меняет не только количественные, но и качественные характеристики поведения резины. Мы обнаружим, что идея об изотропности, вполне себя оправдавшая для ненаполненных резин в области средних и особенно малых деформаций, не годится для шинных резин даже при малых, до 5%, деформациях. В чем причина такого поведения? – ответ на этот вопрос представляется весьма важным, однако его обсуждение выходит за рамки данного исследования. Работы автора в этом направлении опубликованы в [[254], [255]], [256]].
Таблица 2.1.1 Экспериментальные и расчетные данные по двуосному растяжению.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-02-08; просмотров: 634; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.116.118.244 (0.027 с.) |
 ,
,  (2.1.1)
(2.1.1) по оси Y. (Обратим внимание, что l2 является степенью удлинения того размера, который образовался после растяжения образца по оси X, т.е. величины 1/
по оси Y. (Обратим внимание, что l2 является степенью удлинения того размера, который образовался после растяжения образца по оси X, т.е. величины 1/ 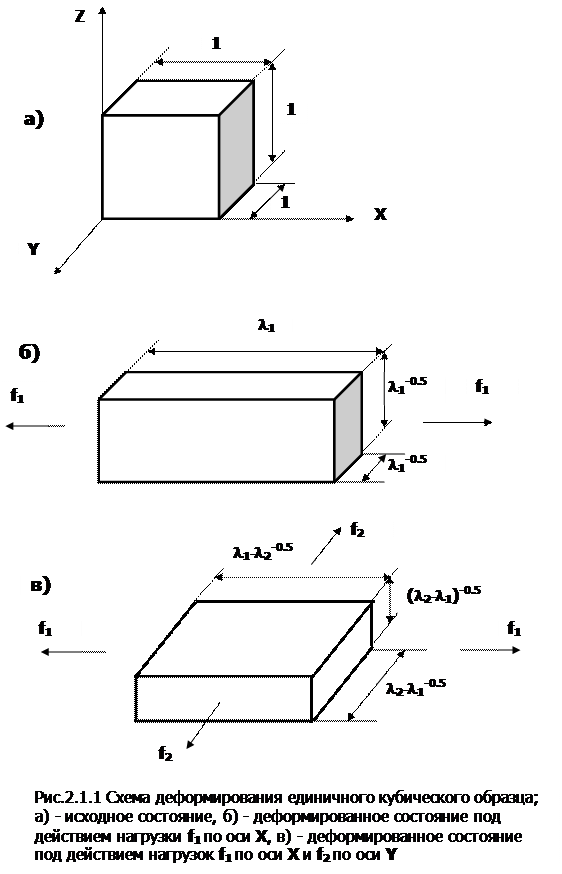
 ;
;  ;
;  . (2.1.2)
. (2.1.2) ;
;  . (2.1.3)
. (2.1.3) . Действительно, для случая упругого деформирования изотропного тела в виде куба равные приложенные нагрузки по двум перпендикулярным осям вызовут равные деформации по этим осям. Приведенные рассуждения справедливы для любых значений l1 = l2, из чегоследует тождество
. Действительно, для случая упругого деформирования изотропного тела в виде куба равные приложенные нагрузки по двум перпендикулярным осям вызовут равные деформации по этим осям. Приведенные рассуждения справедливы для любых значений l1 = l2, из чегоследует тождество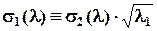 (2.1.4)
(2.1.4)
 (2.1.5)
(2.1.5)




 (2.1.8)
(2.1.8)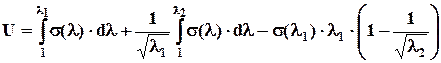 (2.1.10)
(2.1.10) (2.1.11)
(2.1.11)

 ;
;
 =
= 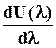 ,
, (2.1.13)
(2.1.13)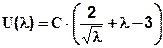 (2.1.14)
(2.1.14)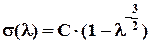 (2.1.15)
(2.1.15)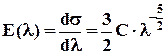 (2.1.16)
(2.1.16) (2.1.17)
(2.1.17) (2.1.18)
(2.1.18) (2.1.19)
(2.1.19)
 (2.1.20)
(2.1.20)


