
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Напряжения и деформации резинокордных слоев
Резинокордное полотно представляет собой конструкцию, образованную наложением нескольких слоев обрезиненных нитей. Число этих слоев может быть достаточно большим, однако основные закономерности механического поведения в полной мере проявляются на двух слоях, каждый из которых представляет собой семейство параллельно расположенных нитей с постоянным шагом (плотностью). В зависимости от угла скрещивания нитей корда двух слоев, их плотности, характеристик резины и нитей корда жесткость конструкции будет различной. Первые работы по исследованию свойств таких систем основывались на нескольких упрощающих предположениях [[76], [77]]. Считалось, что резинокордное полотно находится в условиях плоского НДС. Деформации, как корда, так и резины рассматривались малыми и подчиняющимися закону Гука (1.2.6). Связь между напряжениями и деформациями находили одним из двух альтернативных подходов. Первый заключается в том, что в соответствии с реальной неоднородной конструкцией полотна связь напряжений и деформаций записывается отдельно для резины и нитей корда. Другой путь заключается в том, что конструкция РКК представляется однородным, но анизотропным материалом. При этом усредненные характеристики реального неоднородного и модельного однородного анизотропного полотна являются тождественными. Работа [77] посвящена нахождению уравнений, связывающих напряжения в корде и резине с анизотропными усредненными характеристиками однородного слоя. Диаметр нитей корда является конечной величиной, соизмеримой с расстоянием между нитями. Все расчеты ведутся в пренебрежении местными неоднородностями НДС в непосредственной близи от границы корда, при этом круглое сечение корда заменяется на квадратное равного сечения. Средние деформации, относящиеся к РКК в целом, выражаются через деформации корда и резины с учетом совместности перемещений. С учетом сказанного, в работе получены строгие линейные соотношения, связывающие нормальные и сдвиговые деформации всего резинокордного слоя с характеристиками резины и корда и параметрами структуры полотна. Далее используются два предположения. Первое достаточно очевидно и состоит в том, что модуль корда при одноосном растяжении значительно больше модуля Юнга резины. Второе, согласно которому модуль сдвига резины и обрезиненной нити корда один и тот же, нуждается в дополнительной аргументации. Приведем окончательные выражения, связывающие напряжения и деформации резинокордного слоя:
где h - относительная ширина нити корда (отношение диаметра нити к расстоянию между центрами соседних нитей по нормали), m - коэффициент Пуассона резины. Ось x направлена вдоль нитей корда. Следующий шаг в цитируемой работе – получение соотношений (1.3.1) в виде, не зависящем от выбранной системы координат. Это вопрос технический (см., напр., [[78]]) и мы на нем останавливаться не будем. Далее следует переход от однослойной системы к двухслойной, так как в реальных конструкциях слои часто работают попарно. Здесь автор пользуется принципом независимости НДС слоев, что проявляется в том, что общие напряжения двухслойной системы аддитивно складываются из напряжений каждого слоя, которые различаются только углом ориентации нитей корда. Это предположение может быть использовано лишь для бесконечно малых деформаций по той причине, что деформация одного слоя приводит, вообще говоря, к повороту нитей корда, что скажется на возникновении дополнительных касательных напряжений между слоями. В предлагаемой аддитивной схеме это не учитывается. Следующий шаг – получение уравнений, описывающих поведение двухслойной системы, для произвольной системы координат, что позволяет строить зависимости жесткости от направления растяжения двухслойной системы. Эти уравнения положены в основу предлагаемого экспериментального определения жесткостных характеристик РКК по результатам растяжения двухслойных резинокордных полосок для трех различных значений их ориентации относительно осей симметрии. Метод расчёта, предложенный в данной работе, подробно разобран по той причине, что использованные здесь идеи в той или иной мере фигурируют в большинстве дальнейших исследований, о которых пойдет речь в предлагаемом обзоре. Еще раз перечислим допущения, принятые автором в данной и других работах, выполненных той же школой (см. список литературы в [77]):
1. деформации всех элементов резинокордного полотна являются малыми; 2. зависимости напряжений от деформаций описываются линейным законом; 3. сдвиговая жесткость нитей корда принимается равной сдвиговой жесткости резины; 4. модуль корда на растяжение существенно выше модуля Юнга резины; 5. напряжения двухслойной системы аддитивно складываются из напряжений каждого слоя без учета взаимодействия слоев; 6. НДС резины между нитями корда принимается однородным без учета эффектов вблизи поверхности корда; 7. не рассматриваются повороты нитей корда при растяжении резинокордного слоя.
Описанию свойств однонаправленных резинокордных слоев посвящена монография [[79]], в которой использованы практически те же допущения 1 – 7. Кроме упругих, описаны прочностные свойства композита. Рассмотрены теории максимальных напряжений, максимальных деформаций и их функций для пластиков, армированных жесткими нитями. Объект исследования предполагает малость деформаций, что делает оправданным применение линейной теории. Приведенные экспериментальные данные позволяют заключить о соответствии теории опыту. В обзоре [[80]], кроме свойств однослойных систем, подробно описаны свойства композитов, содержащих до четырех слоев. Для описания деформационных свойств материала применялись уравнения Халпин-Цая. Обращено внимание на явление «твиста» двухслойных систем, связанное с возникновением сдвиговых напряжений в тонкой прослойке резины между слоями. Описаны причины этого явления, заключающиеся в том, что при однородном растяжении резинокордного слоя его прямоугольный фрагмент переходит в параллелограмм, причем угол параллелограмма связан с первоначальной ориентацией нитей корда к оси растяжения фрагмента и степенью его удлинения. Приведено большое число графиков, иллюстрирующих зависимости эффективных модулей однослойных и двухслойных систем в зависимости от параметров системы. Укажем еще несколько работ близкого направления, опубликованных в период активного становления механики многослойных анизотропных РКК. Видимо, первая статья появилась в Германии в 1939 г. [[81]], в которой шина рассматривалась как цилиндр для аппроксимации тороидальной оболочки. Ортотропный композит описывался с помощью модулей эластичности резины и корда. В США этими работами занимался Кларк с сотр. [[82], [83], [84]], в Великобритании Гук [[85], [86]], в Японии Акасака [[87]]. К этому же периоду относятся работы в СССР Бидермана с сотр. [76, 77], обобщенные в монографии [2], переведенной на английский язык и изданной в США. В этой работе, до настоящего времени являющейся настольной книгой механиков и конструкторов шин, исповедуется практически та же идеология, отраженная в пунктах 1 – 7. (Правда, в некоторых случаях учитываются повороты нитей корда при деформировании композита). В этой связи представляется спорным утверждение о хорошем согласии теории с экспериментом [2, с. 63]. В разделе 3.3 будет показано обратное. Вместе с тем авторы утверждают, что на то время отсутствуют достаточно надежные методы расчета усилий и деформаций, возникающих в элементах шины [2, с. 117]. Наконец, отметим работу [[88]], где предпринята попытка изложить минимум сведений, необходимых для выполнения всех основных этапов прочностного расчета оболочечных конструкций из однонаправленных и многослойных анизотропных композиционных материалов. В приложениях даны некоторые программы для ЭВМ на языке Фортран.
В монографии [304] также приводится теория одно- и многослойных эластомеров в применении к задачам расчёта РТИ. Используется линейная теория для описания свойств материалов. Дальнейшее развитие механики шин и РКК пошло не по пути учета нелинейности деформационных зависимостей механических свойств резины и корда. Основные усилия были направлены на совершенствование расчетных схем, позволяющих учитывать геометрическую нелинейность все усложняющейся конструкции пневматической шины [[89]]. Этому способствовало лавинообразное развитие компьютерной техники, что позволило далеко продвинуться в создании расчетных методов механики многослойных анизотропных оболочек [[90], [91]], метода конечных элементов [[92], 12] и метода прямого решения систем дифференциальных уравнений, описывающих деформирование шины [[93]]. Предпринимались попытки перехода от решения упругой задачи к решению вязкоупругой [[94]] и термовязкоупругой [11] задач, продолжая оставаться в линейном приближении по деформациям. И лишь в последнее время появились работы по учету физической нелинейности упругого и вязкоупругого поведения [28, [95], [96]]. Приведем краткий обзор основных направлений современных исследований. Справедливость обычно используемого предположения о линейности закона деформирования корда проверена в работе [[97]]. Прямыми экспериментами показано, что модули упругости корда при весьма малых деформациях более чем в четыре раза отличаются от модулей при разрыве. Расчет НДС шины 175R13 с учетом физической нелинейности корда позволил, в частности, на 25% уточнить силу сопротивления качению. Однако при расчете было принято, что резина является линейным материалом, что оставляет определенное чувство неудовлетворения. В работе [[98]] описываются деформационные характеристики резинометаллокордного полотна. Получены зависимости напряжения от деформации для невулканизованных однослойных и симметричных двухслойных резинокордных образцов. Однако, как и в работе [77], расчетные уравнения базируются на линейности законов деформирования. Нити корда приняты нерастяжимыми и имеющими прямоугольное сечение. Работа имеет скорее прикладной характер, так как авторы предполагали использовать результаты при конструировании сборочных станков для шинного производства.
Вопросу построения матрицы упругости резинокордных слоев посвящена работа [[99]]. На основе модели ортотропного слоистого композита рассчитаны модули в разных направлениях. Свойства резины и корда приняты линейными. Задача решена для зоны борта, в которой многослойная резинокордная оболочка обжата фланцами. Полное решение задачи удалось получить только численно. В работе [[100]] предложен способ экспериментального определения элементов матрицы жесткости ортотропного резинокордного композита, представляющего собой несколько резинокордных слоев, причем нити корда расположены в двух направлениях. Образцы для испытаний представляют собой вырезанные из данного РКК в определенных направлениях «кубики». Эксперимент состоит в испытаниях образцов на растяжение, сжатие, простой сдвиг. Материал корда и резины считается физически линейным, т.к. в процессе испытаний определяются константы жесткости, не зависящие от величины деформации. Это обстоятельство ставит под сомнение предполагаемый выигрыш в точности при применении данной методики. Аналитический расчет упругого деформирования двухслойного резинокордного композита представлен в работе [[101]]. Рассматриваемый образец представлен в виде пяти слоев: двух резинокордных и трех резиновых. Частота нитей корда в явном виде не учитывается, проявляясь в анизотропии однородного слоя и его модулях. Постулируется, что сдвиговые напряжения между слоями действуют строго вдоль оси растяжения образца. Из решения уравнений равновесия для геометрически линейного случая (угол ориентации нитей корда не меняется) и нелинейного (угол меняется) получена зависимость растягивающей нагрузки от удлинения. Полученное решение мало отличается от известных результатов в области реальных значений углов, характерных для брекера. Для той области углов, где жесткость определяется резиной, сравнение с экспериментом не проведено. В этом смысле трудно судить о том, насколько изменится результат, если использовать нелинейные уравнения для описания свойств резины. Хорошим примером использования в методе конечных элементов нелинейных свойств резины служит работа [[102]]. При расчете жесткостных характеристик, напряженного состояния и полей температур резинокордных оболочек высокоэластичных муфт была использована матрица упругости материала, зависящая от достигнутого уровня деформаций конечного элемента. Автор использовал пятиконстантную модель для описания этой нелинейности. Для описания свойств резины в сложном НДС на основе результатов испытаний при одноосном растяжении был применен следующий прием: в полученном уравнении для одноосного растяжения относительное удлинение заменялось величиной интенсивности деформации. Заметим, что такой способ описания сложного НДС не является строгим, т.к. величина интенсивности деформации не является инвариантом тензора деформации, что приводит к зависимости свойств от того, как расположена лабораторная система координат. Несмотря на это, получено хорошее согласие расчета и эксперимента не только для упругой, но и для термоупругой задачи.
Комплексная нелинейная вязкоупругая задача деформирования резинового амортизатора, армированного двумя семействами разнонаправленных малорастяжимых нитей, решена в работе [[103]]. Нелинейные упругие свойства описаны двухпараметрическим степенным потенциалом. В качестве ядра релаксации выбрано ядро Колтунова - Ржаницина. Задача решается численно методом сведения нелинейной краевой задачи к системе алгебраических уравнений в сочетании с приемом деления промежутка интегрирования пополам. В результате решения получены все характеристики амортизатора и их зависимости от расположения армирующих нитей и от упругих и релаксационных параметров резины. Данная работа, по нашему мнению, является уникальной с точки зрения объединения в одном исследовании всех особенностей нелинейного вязкоупругого поведения реального изделия. В близком ключе выполнена работа [95]. Разработанный пакет программ, основанный на использовании МКЭ, позволяет рассчитывать НДС и температурное состояние РТИ, прогнозировать долговечность. К классу решаемых задач относятся: задачи линейной и нелинейной упругости; вязкоупругости; тепловые задачи, включая саморазогрев; контактные задачи с различными условиями трения; задачи усадки и набухания; оценка времени до разрушения. Необходимые параметры моделей определяются встроенными процедурами обработки эксперимента по растяжению лопаток и сжатию цилиндров, кривых релаксации и ползучести, длительной прочности, выносливости стандартных гантелей. Особое внимание уделяется нелинейности (амплитудной зависимости) динамического модуля и подсчету энергии саморазогрева. Работа доведена до коммерческого использования и успешно применяется. В этой связи отметим цикл исследований [[104], [105], [106], [107]], на результаты которых опирались авторы [95]. Следует, однако, подчеркнуть, что долговечность корректнее определять не по показателю усталостной выносливости резиновых гантелей, а по аналогичному показателю образцов с учетом реального НДС, в котором работает данное РТИ. Анализ численного геометрически нелинейного решения оболочечной резинокордной пневматической конструкции проведен в работе [[108]]. Рассмотрены напряжения двухслойной резинокордной торообразной оболочки в геометрически линейной и нелинейной постановках. Использован вариант метода конечных элементов, описанный в [[109]]. Оболочка имеет характеристики, близкие к шинным материалам и нагружается внутренним давлением. Расчеты показали, что различия между решениями линейной и нелинейной задач существенны для сдвиговых напряжений. В монографии [[110]] обобщены многолетние исследования школы Киричевского В.В. в области использования метода конечных элементов в механике эластомеров. В работе [[111]] исследуются жесткостные свойства резинометаллокордных композитов с применением метода Халпин-Цая и метода муара. Изучены образцы с различным соотношением длины и ширины. Установлено, что более эффективным является метод муара. Для расчета по методу Халпин-Цая требуется знать коэффициент Пуассона и модули сдвига корда, однако не приводится метода для достаточно точного их определения. Кроме того, уравнения Халпин-Цая разработаны для композитов с линейными свойствами. Метод муара основан на увеличении точности измерения удлинения образца при растяжении (особенно это важно при малых деформациях), однако воспроизведение этого метода достаточно трудоемко.
|
|||||||||
|
Последнее изменение этой страницы: 2017-02-08; просмотров: 742; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.16.147.124 (0.013 с.) |
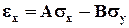 ,
,  ,
, 
 ,
,  , (1.3.1)
, (1.3.1)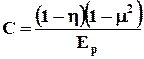 ,
,  ,
,


