
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Тема 1. 4. Оптимізація за багатьма функціями метиСодержание книги
Поиск на нашем сайте
1.4.1. Знаходження компромісного розв’язку
Якщо лінійна задача містить декілька критеріїв оптимізації, то методи лінійного програмування не дають можливості визначити оптимум за багатьма функціями мети. В такому разі доцільно перейти до знаходження компромісного розв’язку, не оптимального ні за жодною з ФМ, але цілком задовільного з точки зору їх сукупності. Умова ефективності компромісного розв’язку формулюється аналогічно до критерія Парето - кожний розв’язок, що не погіршує значень заданих ФМ і призводить до покращення принаймні однієї з них, є ефективним. До найбільш опрацьованих схем компромісу належать умовна підоптимізація і скаляризація. Розглянемо схему умовної підоптимізації. Сукупність ФМ впорядкуємо за спаданням їх вагомості і виберемо f1(x) в якості основної ФМ, а всі інші переведемо в обмеження. В такому разі отримаємо задачу: f1(x) =
fr(x) = xj ³ 0, де r - індекс ФМ; Якщо встановлення значень f1(x) =
xj ³ 0, де br - допустиме відносне погіршення оптимального значення r-ої ФМ (0<br<1). Процес знаходження компромісного розв’язку за методом поступок є багатокроковим з коригуванням на кожному кроці значень br, аж до моменту знаходження задовільного розв"язку. Основними питаннями, що виникають при скаляризації (згортанні векторної функції мети до скалярного виду) є врахування пріоритетів заданих ФМ, знаходження розумного компромісу між ними і знаходження спільної міри різновимірних величин. Скаляризація на основі принципу "справедливого компромісу" полягає у переході від задачі з векторною функцією мети:
до задачі з скалярною функцією мети:
де lr - коефіцієнт вагомості ФМ; gr - коефіцієнти переводу величин до одного виміру;
fr, F r - допустимі межі зміни значення r-ої функції мети. Скаляризація на основі принципу рівномірної оптимізації (справедливого компромісу) полягає у знаходженні такого розв’язку, при якому відносні відхилення значень ФМ від своїх екстремальних значень будуть мінімальними і однаковими. З цією метою будується доповнена задача:
розв’язок якої буде шуканим компромісним. З врахуванням таких змін:
доповнена задача зводиться до лінійного виду:
де Z - максимальне відносне погіршення значень функцій мети; fr* - максимальне значення r-ої функції мети для основної задачі.
1.4.2. Зведення задачі дробово-лінійного програмування до лінійного виду Якщо функція мети є дробово-лінійною, а цей тип функції досить поширений в економічних задачах, то виникає необхідність зведення дробово-лінійної задачі до лінійного виду. Розглянемо один з можливих підходів (метод Нола). Початкова задача має такий вигляд:
Припустимо, що
Після підстановки нових змінних y0, уj в початкову задачу прийдемо до такої лінійної задачі:
Знайшовши оптимальний розв’язок лінійної задачі у0*,уj* з очевидністю отримаємо оптимальний розв’язок початкової задачі:
хj*=уj*у0*.
|
|||||
|
Последнее изменение этой страницы: 2017-02-07; просмотров: 151; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.227.52.111 (0.008 с.) |

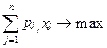 (1.75)
(1.75)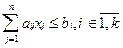 (1.76)
(1.76)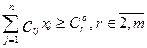 (1.77)
(1.77)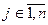 , (1.78)
, (1.78)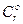 - емпірично встановлене значення r-ої ФМ.
- емпірично встановлене значення r-ої ФМ.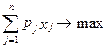 (1.79)
(1.79)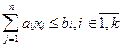 (1.80)
(1.80)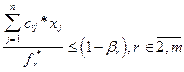 (1.81)
(1.81)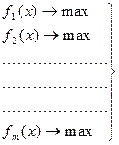 , (1.83)
, (1.83)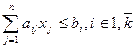 , (1.84)
, (1.84)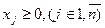 (1.85)
(1.85)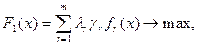 (1.86)
(1.86)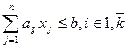 (1.87)
(1.87)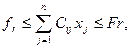 (1.88)
(1.88)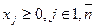 (1.89)
(1.89)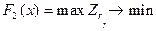 (1.90)
(1.90)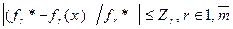 (1.92)
(1.92)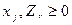 (1.93)
(1.93)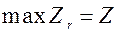 ,
, 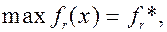
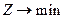 (1.94)
(1.94)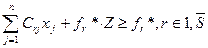 (1.96)
(1.96)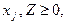 (1.97)
(1.97)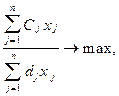 (1.98)
(1.98)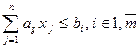 (1.99)
(1.99)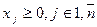 (1.100)
(1.100) і здійснимо таку заміну змінних:
і здійснимо таку заміну змінних: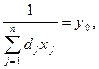 (1.101)
(1.101)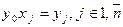 (1.102)
(1.102)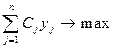 (1.103)
(1.103)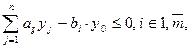 (1.104)
(1.104)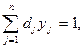 (1.105)
(1.105)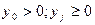 (1.106)
(1.106)


