
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Тема 1. 2. Елементарні перетворення лінійних моделейСодержание книги
Поиск на нашем сайте
ЕС за своєю природою є складною і динамічною. Інерційність ЕС призводить до запізнення в її реагуванні на зовнішні та внутрішні зміни. Часові запізнення також мають місце між моментом здійснення витрат і освоєнням основних фондів, зміною доходів споживачів, цін і попиту на продукцію. Найкоротшим шляхом до побудови складних динамічних моделей є розробка статичних лінійних моделей, які дають моментну характеристику теперішнього або майбутнього стану системи. Для побудови ЕММ слід визначити список основних змінних, функцію мети і систему найсуттєвіших обмежень. Якщо ФМ і обмеження є лінійними функціями, то ЕММ називається лінійною. При відсутності інших застережень будемо вважати всі моделі, які розглядаються нижче, лінійними і детермінованими. Загальна лінійна ЕММ має вигляд:
f(x) =
xj ³ 0, (1.18) де cj, aij, bi - задані сталі величини (bi ³ 0); xj - шукане значення змінної величини; (1.15) - функція мети; (1.16)‑(1.18) - обмеження, що визначають множину допустимих розв’язків задачі.
Розв’язком (допустимим розв’язком) задачі (1.15‑(1.18) називається вектор X=(x1,x2,...,xn), для якого виконуються умови (1.16)‑(1.18). Оптимальним буде допустимий розв’язок, при якому ФМ досягає максимального значення.
Канонічною (основною) називається така модель:
f(x) =
xj ³ 0. (1.21)
Як загальна, так і канонічна модель можуть подаватися у векторній або матричній формах запису. Перехід від загальної до канонічної моделі здійснюється за допомогою додаткових невід”ємних змінних Si, Ui:
Якщо в умові певної задачі є змінна V, на яку не поширюється умова невід”ємності типу (1.21), то для зведення задачі до лінійного виду слід в систему обмежень додатково включити таку умову:
V = V+ - V-, (1.22)
де V+; V- ³ 0.
В лінійній задачі можна без зміни суті задачі поміняти напрям оптимізації, тобто здійснити перехід від задачі на пошук максимуму f(x) до задачі на знаходження мінімуму f(-x), оскільки
max f(x) = ‑min f(-x)
Розглянемо типову задачу виробничого менеджменту - планування оптимального випуску продукції (див.приклад 2 теми1). Будемо вважати, що на підприємстві існує можливість виробництва певної сукупності виробів, кожний з яких користується попитом споживачів. Умови випуску продукції можна описати за допомогою обмеження на виробничі ресурси:
де i - індекс виду ресурсу; j - індекс виду продукції; xj - шукана кількість випуску продукції j-го виду; bi - розмір ресурсного забезпечення. Обмеження на планові значення основних техніко-економічних показників задаються у такому вигляді:
де crj - значення r-го показника; Cr - плановий рівень показника. Попит на продукцію врахуємо шляхом включеня в модель обмеження на границі випуску виробів:
dj £ xj £ Dj, j Î де dj, Dj - нижня, верхня межі випуску продукції j-го виду. В якості функції мети будемо розглядати “максимум прибутку”:
f(x) =
де pj - прибуток на одиницю j-го виробу.
Якщо для початкового розв”язку X=(d1; d2;...dn) умова (1.23) не виконується, то можна стверджувати про первісну неузгодженість умов задачі (1.23)‑(1.26). Якщо для початкового розв”язку X=(D1; D2;...Dn) умова (1.24) не справджується, то можна стверджувати про наявність вторинної неузгодженості умов задачі. Первісна неузгодженість викликається невідповідністю між встановленими нижніми межами випуску продукції і розміром відповідного ресурсногогo забезпечення. Вторинна неузгодженість зумовлюється невідповідністю між встановленими верхніми межами випуску продукції і плановим рівнем показників Cr. Зведемо задачу (1.23)‑(1.26) до канонічного виду:
f(x) =
xj - Sj = dj, j Î xj + Uj = Dj, j Î xj, Si, Ur, Sj, Uj ³ 0. (1.32)
Додаткова змінна Si характеризує використання ресурсу i-го виду. Якщо для розв’язку Xo значення Si=0, то це означає, що в умові задачі і-ий ресурс використаний повністю. Додаткова змінна Ur характеризує розмір перевищення планового завдання по r-му показнику; Sj - розмір випуску продукції j-го виду понад нижню межу dj; Uj - розмір відхилення від верхньої межі виробництва продукції Dj. Якщо умови задачі не узгоджені, то це означає, що не існує таких невід’ємних додаткових змінних типу (1.32), при яких справджуються обмеження (1.28)‑(1.31). Якщо ж додаткові змінні приймають від’ємні значення, то задача (1.27)‑(1.32) виходить за межі задачі лінійного програмування. Скористаємося стандартною заміною змінних, за допомогою якої задача з неузгодженими умовами буде завжди мати допустимий розв’язок. З цією метою виконаємо такі перетворення:
Si = Si+ - Si-, Ur = Ur+ - Ur-, (1.33) Sj = Sj+ - Sj-, Uj = Uj+ - Uj-, (1.34) де Si+ - характеризує залишок ресурсу; Si- - нестачу ресурсу; Ur+ - розмір перевищення планового значення r - го показника; Ur- - розмір недосягнення планового рівня показника; Sj+ - розмір випуску продукції понад нижню межу; Sj- - розмір недосягнення нижньої межі випуску продукції; Uj+ - розмір відхилення від верхньої межі випуску; Uj- - розмір перевищення випуску продукції понад верхню межу. З економічного змісту наведених змінних слідує, що вони попарно заперечують одна одну, тобто якщо одна приймає ненульове значення, то друга обов’язково нульова.
|
||||||
|
Последнее изменение этой страницы: 2017-02-07; просмотров: 153; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.219.87.237 (0.01 с.) |

 cj xj ® max (1.15)
cj xj ® max (1.15) aij xj £ bi, i Î
aij xj £ bi, i Î  (1.16)
(1.16)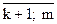 (1.17)
(1.17)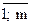 , (1.20)
, (1.20)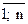 (1.25)
(1.25)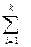 0·Si +
0·Si +  0·Ur +
0·Ur + 


