
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Оптимізація перевезення матеріальних ресурсівСодержание книги
Поиск на нашем сайте Якщо організація складається з територіально віддалених пунктів виробництва і споживання однорідного продукту, то перед нею постає задача формування такого плану перевезення матеріалу, при якому транспорті витрати на поставку продукції були би мінімальними при повному використанні можливостей виробників і задоволенні потреб споживачів. Задача перевезення однорідного продукту (транспортна задача-Т3) з m пунктів виробництва (постачання) в n пунктів споживання описується за допомогою лінійної моделі такого виду:
де xij cij Ai - виробничі можливості i -го постачальника; Bj - розмір потреби j -го споживача в матеріальному ресурсі.
Якщо для задачі(86) - (89) виконується умова
то модель називається замкненою, якщо не виконується - то відкритою. Оскільки кожна транспортна задача, для якої виконується умова (90), має оптимальний розв’язок, то відкриту задачу слід звести до замкненого виду шляхом введення в умову задачі додаткового (фіктивного) пункту виробництва чи споживання продукту. При цьому розмір виробництва (потреби) ресурсу фіктивним пунктом має відповідати розміру розбалансованості умови (90), а витрати на транспортування ресурсу з цього пункту виробництва до усіх пунктів споживання приймаються рівними нулеві. Для знаходження оптимального розв’язку транспортної задачі (86) - (89) можна скористатися симплексним методом, але цей шлях є неефективним. Існують спеціальні методи знаходження оптимального розв’язку ТЗ зокрема модифікований розподільний метод (метод потенціалів). Кожна ТЗ, як задача лінійного програмування, зв’язана з відповідною двоїстою задачею такого виду: z=
де Ui - двоїсті змінні, які відповідають обмеженням (2); V j -двоїсті змінні, які відповідають обмеженням (3).
Розв’язки прямої та двоїстої задач зв’язані між собою такими співвідношеннями:
де
Числа
Приклад 6. Задано два пункти виробництва і три пункти споживання продукту. Потужності виробників, потреби споживачів, а також витрати на перевезення одиниці продукту наведені в табл.4.
Таблиця 4.
Модель транспортної задачі буде мати такий вигляд:
2x11+3x12+5x13+4x21+2x22+3x23 U1 x11+x12+x13=100, U2 x21+x22+x23=150, V1 x11+x21=50, V2 x12+x22=120, V3 x13+x23=80,
Ця задача є замкненою, бо виконується умова (90): 100+150=50+120+80. Опорний розв’язок задачі знайдемо методом подвійної переваги. Першочергово поставка ресурсу здійснюється в клітини, які позначені двома значками переваги V (W), далі - в клітини, які позначені одним значком переваги V, тобто x11=50, x22=120, x23=30. Залишилося заповнити одну клітину x13=50. Цей розв’язок xij= буде опорним, оскільки число базисних елементів (m+n-1=2+3-1), дорівнює числу заповнених клітин(4). Побудуємо двоїсту задачу 100U1+150U2+50V1+120V2+80V3
і перевіримо, чи виконується умова оптимальності для опорного розв’язку. З цією метою розрахуємо потенціали виробників і споживачів, поклавши U1=0. Для заповнених клітин, тобто для клітин в яких U1+V1=2, V1=2, U1+V3=5, V3=5, U2+V3=3, U2= -2, U2+V2=2, V2=4. Переконаємося,чи виконується умова оптимальності для вільних клітин ( 4 + 0 = 4 > 3, умова не виконується, 2 - 2 = 0 < 4, умова виконується. Оскільки умова оптимальності не виконується, то перерозподіляємо поставки. Для цього будуємо з вершинами в клітинах:
Максимальний розмір переміщення ресурсу визначається з умови:
Новий план перевезення матеріалу наведений в табл.5.
Для цього розв’язку умови оптимальності виконуються, отже розв’язок Xij*= є оптимальним, а витрати
є мінімальними. Якщо порівняти ці витрати з витратами на перевезення матеріалу для початкового опорного розв’язку
то можна пересвідчитися, що ефект від оптимізації становить: абсолютний розмір економії
відносний розмір економії
|
||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-02-07; просмотров: 202; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.41 (0.009 с.) |

 , (86)
, (86) , (87)
, (87) , (88)
, (88) , (89)
, (89) - шукана кількість одиниць матеріалу, яка підлягає перевезенню з i -го пункта в j -ий;
- шукана кількість одиниць матеріалу, яка підлягає перевезенню з i -го пункта в j -ий; - витрати на перевезення одиниці матеріалу;
- витрати на перевезення одиниці матеріалу; , (90)
, (90) , (91)
, (91) , (92)
, (92) , (93)
, (93)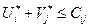 для
для  ,
, для
для 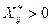 ,
, - оптимальний розв’язок прямої задачі (86)-(89);
- оптимальний розв’язок прямої задачі (86)-(89);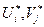 - оптимальний розв’язок двоїстої задачі (91)-(93).
- оптимальний розв’язок двоїстої задачі (91)-(93).

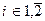
 min,
min,


 ,
, ,
, ,
, ,
, ,
, ,
,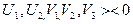 ,
, повинні виконуватися умови:
повинні виконуватися умови: ):
):

 j
i
j
i

 (гр.од.)
(гр.од.) (гр.од.),
(гр.од.), 630-680=-50(гр.од.),
630-680=-50(гр.од.), =
=  =0,0735,(7,35%).
=0,0735,(7,35%).


