
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
История развития методов расчета стержневых систем.. 4Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Первые методы расчетов. 7 Появление классических методов расчета ферм.. 20 Новые методы расчета. 26 Работы в области строительной механики за последние годы.. 31 ОСНОВНАЯ ЧАСТЬ ПРОВЕДЕННОЙ РАБОТЫ... 33 Постановка задачи. 33 Простая балочная ферма. 35 Расчет простой балочной фермы.. 35 Графики прогиба простой балочной фермы.. 41 1.3 Числовой пример простой балочной фермы.. 45 Частота колебаний плоской балочной фермы.. 47 Балочная ферма с параллельными поясами и восходящими раскосами. 51 Расчет балочной фермы с параллельными поясами и восходящими раскосами. 51 Графики прогиба балочной фермы с параллельными поясами и восходящими раскосами 57 Перераспределение жесткостей балочной фермы с параллельными поясами и восходящими раскосами. 61 Числовой пример балочной фермы с параллельными поясами и восходящими раскосами 62 Плоская арочная ферма треугольного очертания. 64 Графики прогиба арочной фермы.. 65 Пространственная ферма балочного типа. 68 Схема конструкции. 68 Расчет пространственной балочной фермы.. 71 Анализ полученного решения. 73 Заключение. 77 Список использованной литературы.. 78 ВВЕДЕНИЕ Прежде всего разберемся в том, что же такое стержневая конструкция, или в ферма. Фе́рма (фр. ferme, от лат. Firmus прочный) — стержневая система в строительной механике, остающаяся геометрически неизменяемой после замены её жёстких узлов шарнирными. В элементах фермы, при отсутствии расцентровки стержней и внеузловой нагрузки, возникают только усилия растяжения-сжатия. Фермы образуются из прямолинейных стержней, соединенных в узлах. Ферма состоит из элементов: пояс, стойка, раскос, шпренгель (опорный раскос). Поиски методов расчета ферм берут свое начало в XIX веке. Первый метод представлен Д. И. Журавским, одни из последних разработаны Такой короткий срок и такая стремительность смены методов объясняются тем, что разработка методов расчета ферм сильно запоздала по сравнению с их практической необходимостью. История развития методов расчета стержневых систем Предпосылки
В 30-х годах XIX века сооружение железных дорог поставило множество задач перед инженерами. К примеру, вес поезда оказался величиной того же порядка, что и постоянная нагрузка, а в деревянных мостах он стал превосходить последнюю. Но, так как положение поезда в разные моменты времени постоянно меняется, то перед инженерами встала задача поиска самого выгодного его положения на мосту и расчета пролетного сооружения при таком, несимметричном положении нагрузки. Интересно отметить, что в 1850 году в Англии исполнилось 25 лет со дня открытия первой железной дороги; во Франции, Германии, Бельгии и США они насчитывают 25 лет существования. Тем более любопытным является тот в факт, что первый метод расчета ферм появился в России, он предшествовал открытию первой большой железной дороги (опыт постройки Царскосельской железной дороги, открытой в 1837 г., не идет в счет, так как на ней не было ни одного большого моста). К решению задачи строительная механика оказалась не готова даже при самой простой схеме моста – балке на двух опорах. Достаточно напомнить, что даже во втором издании курса А. Навье, появившегося в 1833 г., когда в России уже проехал по рельсам паровоз Черепановых, содержалось совершенно ложное представление о работе балки: А. Навье предполагал, что опасное сечение с максимальным моментом всегда находится под центром тяжести внешней нагрузки [1]. Но если для балки расчетные возможности все-таки существовали, то для фермы не существовало никаких расчетных методов. В книгах А. Навье 1833 г. и других подобных книгах были рассмотрены только простейшие ригельно-подкосные схемы, для которых делается условный способ расчета и простая треугольная стропильная ферма. Для балочных ферм второй половины 40-х годов не существовало никаких методов расчета. При этом именно балочная ферма оказалась пригодной для мостов под железные дороги. Схема такой фермы, состоящей из параллельных поясов, соединенных решеткой, впервые была предложена А. Палладио в XVI веке, но не нашла широкого применения до появления железных дорог. В 1820 г. И. Таун дал конструкцию балочной фермы с много решетчатым заполнением, известную до сих пор названием фермы И. Тауна, хотя правильнее ее называть фермой И. П. Кулибина, который применил эту же конструкцию в своем арочном мосту еще в 1772 г. Затем появляются одна за другой фермы Лонга и У. Гау, а Роберт Стефенсон строит известные трубчатые мосты «Британия» и Конуэйский, заменив решетчатое заполнение сплошной стенкой. Именно эти схемы явились родоначальниками современных балочных ферм, при этом историки и инженеры расходятся во мнении, существует ли между ними родовая преемственная связь [1]. В действительности же первые балочные фермы рассматривались современниками именно как балка со сквозной стенкой, а не как новый самостоятельный вид сооружений. Характерной в этом смысле является статья М. С. Волкова, первого русского профессора теоретической механики, опубликованная в 1838 г. Он называет такие фермы «связями» и считает их за балку с выброшенной стенкой [2]. Взамен стенки в «связи» поставлены стойки и раскосы, причем последние служат для предотвращения скольжения.
Рис. 1 - Схемы «связей» (ферм) по М. С. Волкову
Эта статья представляет собой первую попытку анализа ферм, при этом никаких методов расчета в ней представлено не было. Одной из причин отставания развития расчетов ферм по сравнению с арками, помимо практической необходимости, было нахождение науки на старых позициях предельного состояния. Для расчета свода по предельному состоянию можно было без труда выдумать более мене правдоподобные формы разрушения и рассчитывать их статически в состоянии предельного равновесия. Но задача о предельном состоянии статически неопределимой фермы (такими были фермы Палладио и выросшие из них фермы Кулибина-Тауна, Гау и др.) настолько сложна, что и сейчас представляет большие трудности, хотя ученые подходят к ней во всеоружии своих знаний. Для науки XVIII века эти задачи были совершенно неприступны. Поэтому первые методы расчета ферм могли появиться только тогда, когда завершился переход науки на путь расчета по рабочему состоянию, т. е. не ранее 30-40-х годов XIX века. Интересно заметить, что первые правильные методы расчета ферм, как статически определимых, так и статически неопределимых, были даны русскими инженерами [11, 12].
Первые методы расчетов
Работы Д. И. Журавского
Краткая оценка работ Дмитрия Ивановича Журавского в области расчета ферм приведена в «Курсе строительной механики стержневых систем» Д. И. Журавский указывал, что, владея расчетом он доказывал неправильность конструкции стефенсоновских трубчатых мостов, ошибочность мнения Лонга о влиянии предварительного натяжения болтов и ошибочность американских воззрений на сопротивление поясов. Указание на ошибку Лонга интересно тем, что в той задаче Для расчета фермы Гау Д. И. Журавский берет расчетную схему в виде простой раскосной решетки с восходящими раскосами и шарнирными
Рис. 2 - Расчет фермы Гау методом Жуковского
Д. И. Журавский обосновал это пренебрежение тем, что узловые соединения деревянных раскосов не способны воспринимать растягивающие усилия. Д. И. Журавский не начинает с определения опорных реакций фермы, как мы это делаем теперь, а прослеживает судьбу каждого груза от точки его приложения до опор. Возьмем простейший случай: груз Р стоит в среднем узле верхнего пояса. Вырежем узел и найдем из условий равновесия и симметрии сжимающие усилия в раскосах Силы Этот метод расчета интересен с двух точек зрения. Во-первых, он основан на идее вырезания узлов и составлений условий равновесия, и, таким образом, открытие и первое применение метода вырезания узлов безусловно принадлежит Д. И. Жуковскому. Во-вторых, (в этом он отличается от современной формы метода вырезания узлов, идущей от К. Кульмана и Дж. Шведлера), Д. И. Журавский не ищет при вырезании узлов усилий в элементах пояса, а находит разность (равнодействующую усилий в двух смежных панелях, это освобождает от необходимости решения совместных уравнений, хотя в каждом следующем узле встречаются три неизвестных усилия. Идея Д. И. Журавского незаслуженно подверглась впоследствии забвению и могла найти и теперь удачное применение при расчете сложных ферм. В том случае, когла сила Р стоит не в среднем узле, Д. И. Журавский разбирает силу на две части yP и (1- y) P, где y – неопределенный множитель, далее ведет разложение каждой составляющей по узлам в свою сторону. Затем он составляет уравнение равновесия горизонтальных узловых сил и находит из него значение y. Легко заметить, что yP и (1- y) P будут равны опорным реакциям. Расчет раскосной фермы, данный Д. И. Журавским, вполне точен при любом положении нагрузки. В частности, при равномерном загружении всех узлов наибольшее усилие в поясе оказывает равным Далее Д. И. Журавский проводит расчет многопролетной неразрезной фермы. Эта задача статически неопределима
Рис. 3 - Задача Д. И. Журавского
Д. И. Журавский принимает за неизвестную величину перемещение λ точки приложения силы P и находит его из условия равновесия
Откуда углы наклона касательной Работы Дж. Шведлера
Рассмотрим далее работы Дж. Шведлера [4]. В 1851 г. вышла статья, содержавшая метод расчета статически определимых ферм, известный под «методом вырезания узлов» и основанный на составлении условий равновесия для усилий в каждом узле фермы, в предложении его шарнирности. Это был именно тот метод, которым ранее пользовался Д. И. Журавский. Отличие метода Дж. Шведлера в том, что он позволяет обойтись без совместных уравнений лишь в том случае, если возможен такой порядок обхода узлов фермы, при котором в каждом следующем узле встречаются только два неизвестных усилия. Иначе это приводит к совместным уравнениям, число которых равно числу стержней. При этом метод Д. И. Журавского для ферм с параллельными поясами позволяет обойтись без совместных уравнений и в более сложных случаях.
Рис. 4 - Пример фермы, которую легче рассчитать методом Журавского, чем по способу вырезания узлов Дж. Шведлера.
Так для фермы (рис. 4) метод вырезания узлов в простой форме неприменим, так как он приводит к 15 совместным уравнениям с таким же числом неизвестных (при несимметричной нагрузке). Метод вырезания узлов Журавского позволяет сразу найти узловые горизонтальные составляющие, суммирование которых дает усилия в поясах, без всяких совместных уравнений. Подводя итоги, предложенный Дж. Шведлером метод вырезания узлов является, в некотором смысле, повторением способа, ранее найденного Американская техника, заинтересовавшись преимуществами статически определимых ферм, встала во второй половине XIX века на ошибочный путь приближения конструкции ферм к их расчетной схеме и заменила жесткие узлы болтовыми шарнирами. Разумеется, такие фермы обладали пониженной жесткостью и работали плохо, так как их узлы постоянно расстраивались и требовали непрерывного наблюдения и ухода, но тем не менее они применялись в США очень упорно. Это один из немногих примеров в истории строительной механики неправильного понимания взаимной связи между конструкцией и расчетной схемой. Надо отметить, что Дж. Шведлер, увлекаясь изобретенными им способом образования новых схем ферм, старался искать схемы, удовлетворяющие заранее заданным условиям: условию постоянства усилий в элементах пояса фермы с полигональным очертанием (так называется ферма Шведлера), условию минимума веса и т п. Часто выходило, что поиски приводили к схемам, неудобным в конструктивном отношении и потому почти не нашли применения. Кроме того, идея создания фермы наименьшего веса не всегда приводит к наиболее экономичным конструкциям, так как стоимость фермы определяется не только количеством материала в ее исполнении, но и стоимостью труда (которая не пропорциональна весу) и количеством материала в заготовках. При сложных формах элементов раскрой листов дает значительные отходы и потому облегчение веса не всегда уменьшает количество металла, использованного для ее изготовления. Вклад Г. Ламэ
Следующую после Дж. Шведлера попытку расчета ферм мы встречаем в 1852 г. в книге Г. Ламэ. Вопреки легенде, пущенной кем-то из авторов исторических обзоров, Г. Ламэ не рассматривал статически неопределимые фермы, а ограничился статически определимыми, причем применил к их расчету принцип возможных перемещений. Г. Ламе составил на основе известного «принципа Клапейрона» формулу для вычисления перемещений фермы под грузом и искал формы сооружений, дающих минимальный прогиб при условии равнопрочности [1]. Работы Августиновича
Мысль о применении принципа возможных перемещений к расчету ферм использовал русский инженер Августинович [5], распространивший ее на статически неопределимые фермы (1857 г.). Это была первая после В работах Августиновича, в отличие от Д. И. Журавского четко прослеживаются разграничения между статически определимыми фермами и статически неопределимыми. Для расчета статически определимой фермы с n узлами Августинович составляет 2 n уравнений проекции возможных перемещений, задавая их следующим правилом: «если линия наклонна, то пишется ее коэффициент, помноженный на проекцию; а если линия горизонтальна или вертикальна, то пишется коэффициент, наблюдая в отношении знаков, следующее правило: для отдаленных от осей концов линии член пишется с плюсом; для ближайших к осям - с минусом». Под «коэффициентом» понимается усилие в стержне или величина, ему пропорциональная. В приведенных Августиновичем примерах эти «коэффициенты» равны усилиям в стержнях, деленым на их длины.
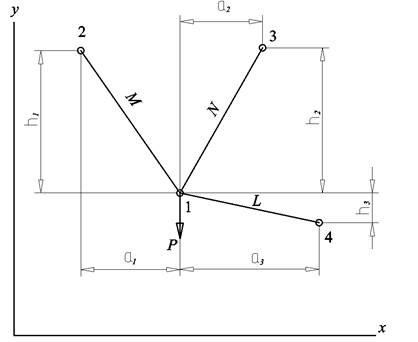
Рис. 5 - Обозначения Августиновича
По этому правилу уравнения перемещений для узла l (рис. 5) примут вид:
Если подставить вместо M, N, L усилия в стрежнях, деленные на длины, мы получим обычные уравнения равновесия. Разумеется, составление и решение системы из 2 n уравнений для фермы с n узлами очень трудоемко (как и метод вырезания узлов в общем случае). Августинович это осознает и заявляет, что на данном этапе развития науки отсутствует метод, который мог бы прийти на помощь в данной ситуации.
Рис. 6 - Первая статически неопределимая ферма, рассчитанная Агустиновичем.
Конечно, способ введенный Августиновичем не облегчал внедрения расчета ферм в проектную практику; с точки зрения трудоемкости он даже представлял некоторый шаг назад. При этом чрезвычайно оригинальным можно считать способ, предложенный Августиновичем для расчета статически неопределимых ферм, поясненный им на примере фермы (рис. 6). Эта распорная ферма имеет при симметричном загружении два лишних неизвестных
Откуда Здесь s – длина элемента пояса; Вместо этого Августинович вспоминает «задачу Жуковского» о действии осевых сил на стержень и обобщает ее, полагая, что к стержню приложены на равных расстояниях продольные силы Применяя закон приложения нагрузок, Августинович вычисляет реакции по концам стрежня:
Затем он доказывает, что решение остается справедливым, если стержень имеет ломаную форму: проекции удлинения системы abcde таковы, как если бы прямой стержень af был натянут силой P. Отсюда Августинович заключает, что вышенаписанные уравнения останутся справедливыми, если вместо сил P подставить горизонтальные составляющие узловых поясных сил, как это делал Д. И. Журавский. При этом реакции, вычисленные по этим уравнениям, будут равны искомым реакциям фермы
Рис. 7 - Лемма Августиновича
Этот способ является довольно оригинальным. Но большого практического распространения, так как расчет является крайне трудоемким. Так или иначе, это первый правильный расчет статически неопределимой фермы.
|
||||||||||||
|
Последнее изменение этой страницы: 2017-02-05; просмотров: 899; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.89.89 (0.011 с.) |


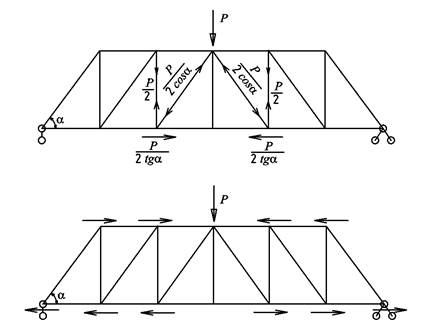
 . Эти усилия передаются на нижние узлы, из равновесия которых находим растягивающие усилия в стойках
. Эти усилия передаются на нижние узлы, из равновесия которых находим растягивающие усилия в стойках  и горизонтальную силу
и горизонтальную силу  , действующую вдоль нижнего пояса. В действительности, эта сила равна разности усилий в двух смежных панелях нижнего пояса, но Д. И. Журавский этим пренебрегает и продолжает процесс вырезания узлов по зигзагу решетки. В результате, он находит усилия во всех раскосах и стойках, и горизонтальные силы, приложенные в узлах и имеющие обратные направления, в отличие от ранее найденных сил
, действующую вдоль нижнего пояса. В действительности, эта сила равна разности усилий в двух смежных панелях нижнего пояса, но Д. И. Журавский этим пренебрегает и продолжает процесс вырезания узлов по зигзагу решетки. В результате, он находит усилия во всех раскосах и стойках, и горизонтальные силы, приложенные в узлах и имеющие обратные направления, в отличие от ранее найденных сил 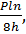 где P – узловая нагрузка, l – пролет, n – число узлов, h – высота фермы. Разумеется, расчет является условным для фермы с перекрестными раскосами, так как выбор однораскосной схемы должен предшествовать расчету, а до его выполнения нельзя установить какой раскос в каждой панели окажется сжатым. Если в результате какой-либо раскос окажется растянутым, то не представит труда заменить его на встречный. При условии такой поправки расчет фермы с перекрестными раскосами будет довольно точным, поскольку раскосы не способны работать на растяжение.
где P – узловая нагрузка, l – пролет, n – число узлов, h – высота фермы. Разумеется, расчет является условным для фермы с перекрестными раскосами, так как выбор однораскосной схемы должен предшествовать расчету, а до его выполнения нельзя установить какой раскос в каждой панели окажется сжатым. Если в результате какой-либо раскос окажется растянутым, то не представит труда заменить его на встречный. При условии такой поправки расчет фермы с перекрестными раскосами будет довольно точным, поскольку раскосы не способны работать на растяжение.
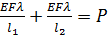 , устанавливая отсюда, что сила P распределяется между участками стержня обратно пропорционально их длинам. Если положение «сечений раздела грузов» в пролетах известно, то предыдущее решение позволяет распределить узловые горизонтальные составляющие между обоими такими сечениями и найти отсюда усилия в поясах. Слабым местом в методе Д. И. Журавского является порядок нахождения этих сечений, для которого он предлагает способ проб, недостаточно обоснованный теоретически. Для неразрезной балочной схемы такими сечениями будут те, в которых касательные к линии прогиба взаимно параллельны. Действительно, условие постоянства длины продольного волокна, отстоящего на y от нейтральной линии, на участке от
, устанавливая отсюда, что сила P распределяется между участками стержня обратно пропорционально их длинам. Если положение «сечений раздела грузов» в пролетах известно, то предыдущее решение позволяет распределить узловые горизонтальные составляющие между обоими такими сечениями и найти отсюда усилия в поясах. Слабым местом в методе Д. И. Журавского является порядок нахождения этих сечений, для которого он предлагает способ проб, недостаточно обоснованный теоретически. Для неразрезной балочной схемы такими сечениями будут те, в которых касательные к линии прогиба взаимно параллельны. Действительно, условие постоянства длины продольного волокна, отстоящего на y от нейтральной линии, на участке от  до
до  выразится:
выразится:
 в точках
в точках 

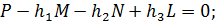

 и
и  . Для их определения необходимо составить два условия деформации, выражающие постоянство длин проекции на горизонтальную ось обоих поясов. При постоянной длине панели и равенстве сечений элементов пояса (допущения Августиновича) можно составить условия равенства нулю суммы проекций удлинений поясов в виде:
. Для их определения необходимо составить два условия деформации, выражающие постоянство длин проекции на горизонтальную ось обоих поясов. При постоянной длине панели и равенстве сечений элементов пояса (допущения Августиновича) можно составить условия равенства нулю суммы проекций удлинений поясов в виде:
 т. е. алгебраическая сумма усилий в элементах каждого пояса должна быть равна нулю.
т. е. алгебраическая сумма усилий в элементах каждого пояса должна быть равна нулю.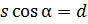 – длина панели; N – усилие в элементе пояса.
– длина панели; N – усилие в элементе пояса. .
.
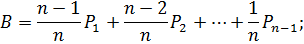
 в зависимости от того, для какого узла пояса взяты узлы.
в зависимости от того, для какого узла пояса взяты узлы.



