Появление классических методов расчета ферм

 

Рассмотрим появление классических методов расчета ферм.

Одновременно с работой Августиновича, содержащей первый правильный способ расчета статически неопределимой фермы, в 1857 г. вышла книга Г. Шеффлера, предлагающая неверный метод расчета многорешетчатых ферм, основанный на учете изгиба всей фермы, как и балки. Г. Шеффлер решил, что при изгибе фермы с радиусом кривизны R каждый раскос изогнется с радиусом кривизны , где – угол наклона раскоса к поясу. Исходя из этого предположения, он подсчитывал общий момент изгиба всей фермы – поясов и раскосов. Насколько известно, к этому способу расчета в дальнейшем никто не обращался. Взамен этого расчета многорешетчатых ферм (Ф. Гербер в 1865 г., Лесль и Шюблер в 1871 г.) окончательно установили условный способ, который с некоторым поправками дожил до сегодняшних дней: пояса и рассчитываются по изгибающим моментам, а раскосы по поперечной силе, деленной на число решеток [1].

 

Работы У. Дж. Ренкина

 

В 1858 г. появляется новая идея расчета статически определимой фермы, которая позже (1964 г.) [6] привела к открытию Максвеллом знаменитого графического приема, известно под именем диаграммы Кремоны – Максвелла. Эта идея принадлежала У. Дж. Ренкину и была позднее (1862 г.) изложена им в его широко известном в свое время «Руководстве для инженеров-строителей».

Идея У. Дж Ренкина состоит в том, что ферма рассматривается как веревочный многоугольник, по которому строится силовой многоугольник. Этот прием поясняется примером, приведенным в книге У. Дж. Ренкина
(стр. 196-198 русского издания). Для стропильной фермы (рис. 8) строится силовой многоугольник с полюсом в т. О, проводя лучи, параллельные элементам нагружного обвода фермы. При этом отрезки AB и DE, выразят реакции опор, а их сумма равна грузу P. Весь отрезок, по словам Ренкина,
«… означает то, чем должен быть груз в точке 1 для того, чтобы условия равновесия брусьев A и E были исполнены, и, следовательно, BD представляет недостаток действительного груза в точке 1 или придаточную отвесную силу, действующую вниз: она-то и должна быть заменена раскашиванием. BD противоположное и равное DB представляет равнодействующую недостатка поддерживающих усилий в точках 3 и 4, в которых нет действительных грузов». Проводя лучи DC и BC, паралелльные раскосам, до пересечения в точке С, можно найти усилия во всех стержнях фермы.

Рис. 8 - Графический расчет фермы по У. Дж. Ренкину

Идея У. Дж. Ренкина состоит в построении графика, в котором отрезки параллельны соответственным стержням фермы и равны усилиям в них (при определенном силовом масштабе), причем график не содержит ни одной лишней линии. В этом смысле график У. Дж. Ренкина является предпосылкой для создания диаграммы Л. Кремоны. Но последняя представляет многоугольник, взаимный с фермой, в том смысле, что каждому узлу одной фигуры отвечает замкнутый многоугольник другой, и обратно, то диаграмма У. Дж. Ренкина этим свойством взаимности не обладает, и поэтому ее нельзя построить путем последовательного обхода узлов фермы.

 

Вклад А. Риттера

 

В 1862 г. вышла книга Августа Риттера [7], в которой был впервые изложен метод сечений или моментных точек. В отличие от метода вырезания узлов этот метод позволял (для ферм, образованных из треугольников) непосредственно вычислить усилие в любом стержне вне зависимости от прочих и без решения совместных уравнений. Этим резко снижалась трудоемкость расчета. По существу, это был первый действительно удобный и общедоступный способ расчета ферм. 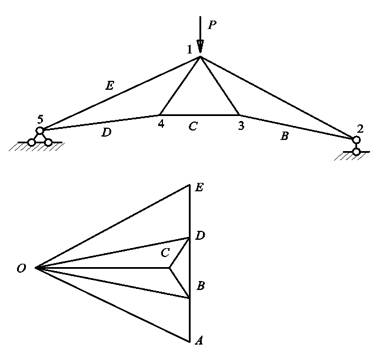Кроме того, его важным достоинством является возможность представления усилия в любом стержне стандартным выражением , где M - момент внешних сил относительно моментной точки, а r – плечо стержня относительно той же точки. Такое представление объясняет характер работы каждого стержня и его роли в работе всей фермы. Впоследствии оно сильно упростило задачу построения линий влияния для стержневой системы. Метод сечений приобрел популярность среди инженеров-проектировщиков.