Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Работы Дж. К. Максвелла и его «дублеров»Содержание книги
Поиск на нашем сайте
Дж. К. Максвелл в 1864 г. публикует знаменитый графический метод, который через 8 лет независимо от него был открыт итальянцем Л. Кремоной (1872 г.). В последствии метод назван диаграммой Кремоны-Максвелла. Открытый Дж. К. Максвеллом способ вычисления перемещения ферм был заново открыт в более общем виде Мором и известен под названием формулы Мора-Максвелла или просто формулы Мора [12]. Открытый Рассмотрим более подробно метод расчета статически неопределимых ферм, предложенный Дж. К. Максвеллом. Его особенностью было представлений уравнений деформации в канонической форме и указание общего метода вычисления перемещений, которые являются коэффициентами в этих уравнениях. В настоящее время под каноническими уравнениями метода сил понимают систему уравнений вида:
выражающих условия отсутствия перемещений по направлениям лишних связей в n -кратно статически неопределимой системе. Здесь В 1864 г. Дж. К. Максвелл составляет канонические уравнения для статически неопределимых ферм в развернутом виде, т. е. с готовыми выражениями коэффициентов. В подлинных обозначениях они примут вид:
Здесь P – нагрузка, R, S, T,…- усилия в лишних связях; r, s, t,…, p – усилия в стержнях от единичных сил R =1, S =1, T =1,…, P =1; e – удлинение стержней от единичного в них усилия. В переводе на обычные обозначения:
Таким образом, Дж. К. Максвелл сумел дать простой способ вычисления перемещений для ферм. Из этого способа сразу вытекает теорема о взаимности перемещений:
Работы Дж. К. Максвелла и его «дублеров» завершили поиски удобных методов расчетов ферм как статически определимых, так и неопределимых.
Новые методы расчета
Появление классических методов расчета ферм позволило инженерам рассчитывать фермы обоих классов, как статически определимые, так и статически неопределимые. Однако степень трудоемкости расчетов была неравнозначной. В статически определимых фермах расчет предшествует подбору сечений, так что конструктор точно подбирает эти сечения, зная величины усилий в каждом элементе. В статически неопределимых фермах подбор сечений должен предшествовать расчету, т. е. этими сечениями необходимо задаваться предварительно, не имея представлений о величине усилий. Поэтому последующий расчет обычно показывает несоответствие между усилиями и сечениями стрежней и их приходится изменять, а затем снова проводить расчет. Эту операцию иногда необходимо проводить множество раз, прежде чем можно получить необходимое соответствие между усилиями и сечениями. Сам процесс расчета статически неопределимой фермы заметно сложнее, чем для статически определимой, особенно при наличии нескольких связей, приводящей к системе совместных уравнений. Таким образом, ставится задача оптимизации полученных методов и их упрощению в использовании. Разумеется, с общим ростом математической культуры инженеров изменяется оценка «трудоемкости» расчетов; приемы, затруднявшие передовых инженеров 100 лет назад, теперь не кажутся трудными даже рядовому технику. Но тенденция к упрощению расчетных приемов продолжает существовать и вероятно никогда не исчезнет. Если перед инженером имеются два варианта сооружения, более или менее равноценные по всем показателям, но с абсолютно различной степенью трудоемкости расчета, он обычно предпочтет вариант, допускающий более простой расчет. Именно этим можно обусловить потерю интереса в последней четверти XIX века к статически неопределимым фермам. Создается своеобразное положение, которое отмечалось в исторической литературе: пока инженеры вообще не умели рассчитывать фермы, они строили исключительно статически неопределимые фермы; когда же им указали, как надо такие фермы рассчитывать, они перестали их применять. Этому факту не противоречит продолжавшееся до конца века применение двухраскосных ферм, хотя в быстро убывающем количестве; дело в том, что расчет таких ферм осуществлялся путем разложения на простые решетки, т. е. их рассчитывали, как статически неопределимые. Применение ферм в мостостроении поставило перед инженерной наукой очередную задачу – расчет ферм на подвижную нагрузку. Эту задачу пытался разрешить еще Д. И. Журавский, но ему это не удалось. Решение затянулось на многие годы и было найдено в методе линий влияния. Методика построения линий влияния зародилась в 1854 г. Бресс составил таблицы «чисел влияния» для распора и опорных моментов бесшарнирной арки, высказал идею их использования путем наложения отдельных сил. Бресс часто применял принцип независимости действия сил, вытекающий из линейности основных уравнений строительной механики. Через 13 лет после Бресса линии влияния для балки с заделанными концами построил Г. Винклер [10] (1867 г.); в 1868 г. он построил их для арки, доведя до конца идею Бресса и заслужив славу изобретателя линий влияния. Любопытно заметить, что все эти попытки построения относились к статически неопределимым системам, прошло много лет, прежде чем додумались до их применения к статически определимой балке (Френкель 1876 г.). После этого перейти к балочной ферме было уже нетрудно, так как метод моментных точек фактически сводил задачу расчета фермы к расчету простой балки. В сущности, все дальнейшие усилия ученых были направлены на расчет сложных ферм описанных ранее классов, структурные особенности которых заключаются в том, что они образованы не из треугольников. Ввиду этого расчет их по способу вырезания узлов или по способу моментных точек приводил к совместным уравнениям, что сильно осложняло задачу. Такие сложные статически определимые фермы почти не нашли применения в строительстве, так как не обладали особыми преимуществами перед простыми фермами. Для решения сложных задач применялись метод моментных точек Мюллера-Бреслау (1887 г.), Абрамова (1935 г.); метод замены стержней Геннеберга (1886 г.); метод замены связей (1901 г.); метод ложного положения. В отличии от теории статически определимых ферм, история расчета статически неопределимых ферм не остановилась на методе Максвелла-Мора и далека до совершенства в наши дни. Расчеты статически неопределимых ферм связаны с трудностями. Если увеличивать площадь сечения одного лишнего стержня, оставив сечения всех прочих стержней неизменными, то усилие в этом стержне возрастет; если уменьшить его сечение, уменьшится и усилие.
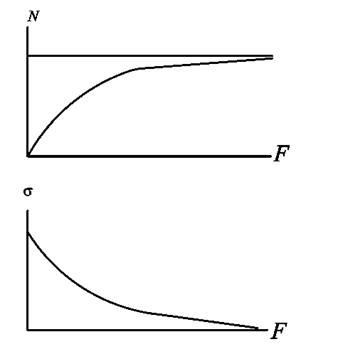
Рис. 9 - Зависимость усилия и напряжения в стрежне от площади его сечения
На рис. 9 наглядно представлен частный случай из теоремы Мориса-Леви о невозможности обеспечить для лишних стержней напряжения заданной величины. Важной попыткой устранить практические неудобства теоремы Максвелла-Мора следует считать «метод заданных напряжений». Он был предложен в 1928 г. немецким инженером Гейманом и получил значительное развитие в работах И. М. Рабиновича, К. М. Зуберяна, Ю. А. Радцига. Метод состоит в том, что мы не задаемся размерами сечений, а величинами напряжений во всех основных стержнях, после чего усилия в лишних стержнях определяются из раздельных уравнений без необходимости совместного решения. В дальнейшем было доказано падение несущей способности сжатых стержней после потери устойчивости, что эквивалентно хрупкому излому, т. е. мгновенному выходу из строя. Таким образом, расчет статически неопределимой фермы по предельному состоянию возможен лишь в том случае, если в процессе перехода фермы от рабочего к предельному состоянию ни один сжатый стержень не потеряет устойчивости. В результате приходится признать, что задача расчета статически неопределимых ферм до сих пор является актуальной задачей, в особенности для случая подвижной нагрузки.
|
||||||||||||
|
Последнее изменение этой страницы: 2017-02-05; просмотров: 284; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.138.124.123 (0.006 с.) |

 …………………………………………………
…………………………………………………

 – неизвестные усилия в лишних связях;
– неизвестные усилия в лишних связях;  – перемещение по направлению связи I от единичной силы в связи k;
– перемещение по направлению связи I от единичной силы в связи k;  – перемещение от внешней нагрузки по направлению связи i.
– перемещение от внешней нагрузки по направлению связи i.



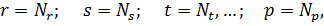 а, следовательно, коэффициенты уравнений Дж. К. Максвелла могут быть выражены следующим образом:
а, следовательно, коэффициенты уравнений Дж. К. Максвелла могут быть выражены следующим образом: и т. д.
и т. д.