
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Расчет пространственной балочной фермыСодержание книги
Поиск на нашем сайте
Алгоритм составления системы уравнений метода вырезания узлов основан на вычислении направляющих косинусов усилий, вычисляемых по заданным координатам, и организации их записи в матрицу
где Компоненты вектора нагрузок с номерами
Матрица направляющих косинусов
Вектор нагрузки, равномерно распределенной по верхнему поясу, имеет вид:
Решение системы линейных уравнений (60) ищем в символьном виде, используя систему Maple:
где
где
Коэффициент
Решение уравнения (3) было найдено оператором rsolve. Проверка полученного решения проводится на фермах с произвольным числом панелей по численному решению, проводимому по той же программе, но в численной моде.
Анализ полученного решения
Рассмотрим зависимость прогиба фермы от числа панелей k при фиксированной длине половины пролета
Рис. 30 -
Рис. 31 - Решение (2) при любой нагрузке легко обобщается на случай, когда жесткость стержней поясов и решетки разная. Обозначим жесткости продольных стержней нижнего и верхнего пояса длиной
Еще одна интересная и необычная особенность конструкции — смена знака усилий в стержнях среднего контура при изменении четности числа панелей. Это следует из полученного аналитического решения. Так, усилие в нижнем стержне среднего контура имеет вид: В заключении отметим еще одну особенность данной конструкции. Для несимметричного варианта фермы Выводы Получены компактные и точные формулы для определения вертикального прогиба фермы под действием сосредоточенной и равномерно распределенной по узлам нагрузки. Замечено, что в случае одной сосредоточенной силы последовательность решений метода индукции, из которой можно вывести общую формулу для произвольного числа панелей, несколько короче, чем для распределенной нагрузки. Обнаружено влияние четности числа панелей в половине пролета на знаки усилий в среднем контуре и вырождение системы при нечетном числе панелей в пролете фермы.
Заключение В данной работе для плоской балочной фермы и для балочной фермы с параллельными поясами и восходящими раскосами были получены значения прогиба при различных вариантах нагружения, исследована деформация центрального узла фермы в зависимости от числа панелей и номера нагруженного узла. Исследована возможность уменьшения прогиба за счет изменения жесткостных параметров системы. Исследована зависимость собственной частоты колебаний от номера узла, в котором закреплен груз и числа панелей. Также был проведен анализ плоской арочной фермы треугольного очертания. В результате чего были получены выражения для прогиба и графики зависимостей прогиба. Была исследована конструкция пространственной фермы балочного типа, произведен ее расчет, проанализировано полученное решение. Получены компактные и точные формулы для определения вертикального прогиба фермы под действием сосредоточенной и равномерно распределенной по узлам нагрузки. В ближайшей перспективе – создать модели рассмотренных ферм в САПР SolidWorks, провести их прочностной расчет и сравнить новые данные с полученными до этого аналитически.
Список использованной литературы 1. Jiang H., Kirsanov M.N. An analytical expression for the influence line of the truss 2. Dong Xiaomeng, Kirsanov M.N. The dependence of the deflection of the truss from the // Вестник научных конференций. 2016. № 1-4(5). С. 6-7 3. Кирсанов М.Н. «Формулы для расчета плоской балочной фермы с произвольным числом панелей» // Строительная механика и конструкции. 4. Кирсанов М.Н. Аналитическое исследование прогиба плоской балочной фермы под действием равномерной нагрузки [Электронный ресурс] // Моделирование и механика конструкций. 2016. №3 5. Кирсанов М.Н. Аналитический расчет, предельный и сравнительный анализ плоской балочной фермы // Научный вестник ВГАСУ. Строительство и архитектура. 2015. №3(39). С. 86-93. 6. Голоскоков Д.П. Практический курс математической физики в системе Maple. СПб.: Изд-во ПаркКом, 2010. 644 с 7. Кирсанов М.Н. Maple и Maplet. Решения задач механики. СПб.: Изд-во Лань, 2012. 512 с 8. Кирсанов, М. Н. Индуктивный метод решения статики и динамики стержневых систем / М. Н. Кирсанов // Международный форум информатизации. МФИ—2001. — С. 163—166 9. Реутов, Д. О. Индуктивный анализ прогиба фермы регулярной структуры в системе Maple / Д. О. Реутов // Международная научно-практическая конференция ИТОН—2014. IV междунар. науч. семинар и междунар. школа по математическому моделированию в системах компьютерной математики «KAZCAS— 2014»: материалы конф. и тр. семинара. — Казань: Фолиант, 2014. — С. 256—261. 10.. Дзабиев, А. А. Формулы для расчета прогиба арочной фермы / А. А. Дзабиев, С. П. Черепанов // Вопросы образования и науки: теоретический и методический аспекты: сб. науч. тр. по материалам Меж- дунар. науч.-практ. конф., 31 мая 2014 г. Ч. 4. 11. Бернштейн С.А. «Очерки по истории строительной механики» М.: Госстройиздат, 1957. 236 с. 12. «Советская наука и техника за 50 лет» книга «Развитие механики в СССР» под редакцией академика А. Ю. Ишлинского 13. СНиП 2.01.07-85 14. ГОСТ 8239-89
|
|||||||||||||
|
Последнее изменение этой страницы: 2017-02-05; просмотров: 286; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.220.242.160 (0.008 с.) |

 . Уравнения равновесия сводятся к системе, которую запишем в матричной форме
. Уравнения равновесия сводятся к системе, которую запишем в матричной форме ,
, – вектор усилий в стержнях,
– вектор усилий в стержнях, 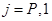 ,
, 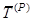 – вектор заданных нагрузок,
– вектор заданных нагрузок,  – вектор нагружения системы, соответствующий единичной силе.
– вектор нагружения системы, соответствующий единичной силе. соответствуют направлениям силы вдоль оси
соответствуют направлениям силы вдоль оси  , с номерами
, с номерами 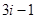 – вдоль оси
– вдоль оси  , а с номерами
, а с номерами 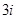 – вдоль оси
– вдоль оси  . Здесь
. Здесь  Для уравнений равновесия потребуются проекции стержней-векторов на оси координат и их длины:
Для уравнений равновесия потребуются проекции стержней-векторов на оси координат и их длины: ,
,  .
.
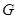 имеет компоненты:
имеет компоненты:


 .
.
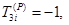 где i изменяется в пределах:
где i изменяется в пределах:
 , где
, где  — обратная матрица. Результатом работы программы являются аналитические выражения для усилий в стержнях фермы. Для вычисления прогиба воспользуемся формулой Максвелла-Мора:
— обратная матрица. Результатом работы программы являются аналитические выражения для усилий в стержнях фермы. Для вычисления прогиба воспользуемся формулой Максвелла-Мора:
 – модуль упругости стержней,
– модуль упругости стержней,  – площадь сечения стержней (одинаковые для всей конструкции),
– площадь сечения стержней (одинаковые для всей конструкции),  и
и  – длина j -го стержня и усилие в нем от действия заданной нагрузки,
– длина j -го стержня и усилие в нем от действия заданной нагрузки, 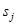 — усилия от единичной вертикальной силы, приложенной к середине пролета в верхнем поясе. Суммирование ведется по всем стержням фермы, кроме опорных, которые предполагаются жесткими. Введем обозначение
— усилия от единичной вертикальной силы, приложенной к середине пролета в верхнем поясе. Суммирование ведется по всем стержням фермы, кроме опорных, которые предполагаются жесткими. Введем обозначение  . Методом индукции получим относительный прогиб верхнего узла фермы:
. Методом индукции получим относительный прогиб верхнего узла фермы: , (35)
, (35) ,
,  ,
,  ,
,
 ,
,  ,
, .
. получен в системе Maple обобщением последовательности 27, 182, 659, 1768, 3919, 7638, 13551, 22400, 35027,…, 192038. Чтобы получить закономерность, потребовалось рассчитать последовательность из 16 ферм. Для нахождения общего члена последовательности применялась функция rgf_findrecur из пакета genfunc, возвращающая рекуррентное уравнение:
получен в системе Maple обобщением последовательности 27, 182, 659, 1768, 3919, 7638, 13551, 22400, 35027,…, 192038. Чтобы получить закономерность, потребовалось рассчитать последовательность из 16 ферм. Для нахождения общего члена последовательности применялась функция rgf_findrecur из пакета genfunc, возвращающая рекуррентное уравнение: .
. и заданной суммарной нагрузке
и заданной суммарной нагрузке  . Прогиб отнесем к значению суммарной нагрузки:
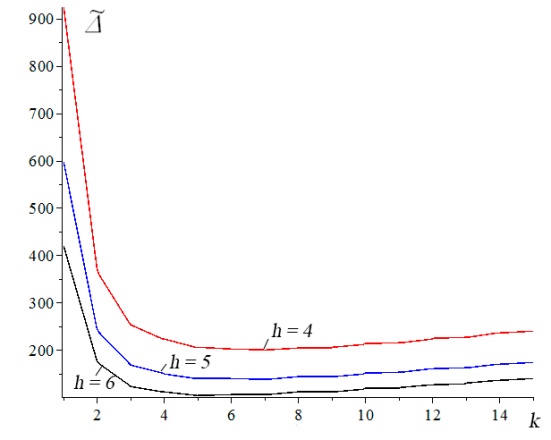
. Прогиб отнесем к значению суммарной нагрузки:  . Соответствующие кривые (рис. 30, размеры в метрах) обнаруживают ожидаемый результат — увеличение высоты h приводит к увеличению жесткости конструкции. С увеличением параметра
. Соответствующие кривые (рис. 30, размеры в метрах) обнаруживают ожидаемый результат — увеличение высоты h приводит к увеличению жесткости конструкции. С увеличением параметра  жесткость падает. Значительно интереснее зависимость прогиба от числа панелей. В данной конструкции она немонотонная, что объясняется «мигающими» слагаемыми вида
жесткость падает. Значительно интереснее зависимость прогиба от числа панелей. В данной конструкции она немонотонная, что объясняется «мигающими» слагаемыми вида  в коэффициентах решения. Кроме того, если не обращать внимание на резкое падение кривой в начале графика, соответствующее неестественно длинным панелям (
в коэффициентах решения. Кроме того, если не обращать внимание на резкое падение кривой в начале графика, соответствующее неестественно длинным панелям ( при высоте фермы
при высоте фермы  или
или  ), то можно заметить почти линейное нарастание прогиба, свидетельствующее о наличии наклонной асимптоты. Методами Maple (оператор limit) легко получить тангенс угла наклона асимптоты:
), то можно заметить почти линейное нарастание прогиба, свидетельствующее о наличии наклонной асимптоты. Методами Maple (оператор limit) легко получить тангенс угла наклона асимптоты: 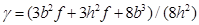 и саму асимптоту
и саму асимптоту  , где
, где  . Коэффициент
. Коэффициент  зависит от четности числа панелей:
зависит от четности числа панелей:  для четных k и
для четных k и  для нечетных.
для нечетных.


 номером 1, стержней решетки нижнего пояса длиной
номером 1, стержней решетки нижнего пояса длиной  — 2, боковых решеток — 3, стержней среднего контура длиной
— 2, боковых решеток — 3, стержней среднего контура длиной  — 4. Выразим жесткости стержней через некоторую приведенную жесткость:
— 4. Выразим жесткости стержней через некоторую приведенную жесткость:  . В этом случае из (2) следует:
. В этом случае из (2) следует: .
.
 усилия в боковых стержнях контура:
усилия в боковых стержнях контура: 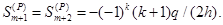 Этот факт следует учитывать при расчете стержней на прочность и устойчивость.
Этот факт следует учитывать при расчете стержней на прочность и устойчивость. , когда треугольный контур нельзя расположить в плоскости симметрии, оказывается, что определитель матрицы системы уравнений равновесия равен нулю. Из численного анализа это можно и не заметить, что приведет к ошибочному решению. Аналогичный эффект ранее был обнаружен в пространственной осесимметричной конструкции и плоской решетчатой ферме.
, когда треугольный контур нельзя расположить в плоскости симметрии, оказывается, что определитель матрицы системы уравнений равновесия равен нулю. Из численного анализа это можно и не заметить, что приведет к ошибочному решению. Аналогичный эффект ранее был обнаружен в пространственной осесимметричной конструкции и плоской решетчатой ферме.


