
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Расчет простой балочной фермыСодержание книги
Поиск на нашем сайте
Для определения прогибов стержневой системы требуется найти усилия во всех стержнях. Задача определения усилий в стержнях фермы сводится к решению системы линейных уравнений, которую можно записать в матричной форме:
Здесь
Этот метод хорошо реализуется в системе компьютерной математики Maple [6, 7]. В поставленной задаче таких нагрузок две: первая – это внешняя вертикальная нагрузка, приложенная поочередно к каждому узлу нижнего пояса фермы, начиная со второго до центрального; вторая – единичная вертикальная нагрузка в центральном узле нижнего пояса, где определяется прогиб. В первый узел нагрузка не прикладывается, так как находится в шарнирном закреплении. Введем обозначение для усилий в стержнях фермы. Усилия от внешней нагрузки обозначим
В первом приближении жесткости
Рис. 11 - Номера стержней и узлов фермы при n = 4, j = 3
На рис. 11 представлены номера стержней и узлов фермы при Пронумеруем шарниры фермы (нижний пояс слева направо, затем верхний пояс (рис. 11). Выбирая начало координат в левой неподвижной шарнирной опоре, зададим координаты шарниров
Стержни решетки фермы зададим условными векторами Для стержней имеем следующие векторы: Горизонтальные:
Наклонные:
Вертикальные стержни:
Опоры:
Длины стержней и проекции их векторных представлений на оси координат:
Первый индекс в номере Матрица направляющих косинусов
где
Где Приведем пример зависимостей, полученных с помощью оператора rgf_findrecur [6,7] системы Maple для прогиба от номера нагруженного узла. Ферма с 9 панелями, нагрузка приложена поочередно к каждому узлу нижнего пояса, начиная со второго:
Ферма с 11 панелями, нагрузка приложена поочередно к каждому узлу нижнего пояса, начиная со второго:
Ферма с 13 панелями, нагрузка приложена поочередно к каждому узлу нижнего пояса, начиная со второго:
Продолжая далее до n = 23, находим зависимость. Проанализировав полученные данные, можно сделать вывод о том, что в формулах для прогиба с разным числом панелей n меняется только коэффициент при
где Далее введем замену, чтобы перейти от
Подставив (15) в (12), получена формула:
Формула (16) может быть использована для вычисления прогиба центрального узла данной балочной фермы для любого нечетного n и нагрузке, приложенной к любому из узлов нижнего пояса. Для того чтобы избавится от ограничения по четности, методом, описанным выше, получена формула прогиба центрального узла от числа панелей при нагрузке, приложенной в «центр»:
Стоит заметить, что если в (16) подставить Система компьютерной математики Maple [6, 7] при помощи функции piecewise [6, 7] позволяет записать неэлементарную функцию, отвечающую наложенным условиям вида:
|
|||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-02-05; просмотров: 404; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.117.75.53 (0.009 с.) |

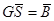 .
.
 – вектор неизвестных усилий длиной
– вектор неизвестных усилий длиной  , где
, где 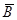 – вектор нагрузок,
– вектор нагрузок,  – матрица направляющих косинусов. Горизонтальные нагрузки, приложенные к узлу
– матрица направляющих косинусов. Горизонтальные нагрузки, приложенные к узлу  , записываются в нечетные элементы
, записываются в нечетные элементы  , вертикальные – в четные
, вертикальные – в четные  . Решение находим с помощью обратной матрицы:
. Решение находим с помощью обратной матрицы: .
.
 усилия от единичной вертикальной нагрузки в центральном узле
усилия от единичной вертикальной нагрузки в центральном узле  . Прогиб определяется по формуле Максвелла – Мора [17]:
. Прогиб определяется по формуле Максвелла – Мора [17]:
 всех стержней приняты одинаковыми. Так же для упрощения выражений введено следующее обозначение
всех стержней приняты одинаковыми. Так же для упрощения выражений введено следующее обозначение  , где
, где  и
и 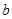 —геометрические параметры фермы, длина панели и высота соответственно. Применим метод индукции и последовательно решим в символьной форме поставленную задачу для фермы с 1, 2, 3 и т. д. панелями. Для каждого варианта определим прогиб при нагрузке, приложенной поочередно в каждый узел нижнего пояса. Сначала найдем последовательности целочисленных коэффициентов перед соответствующими выражениями, а затем и их общие члены при
—геометрические параметры фермы, длина панели и высота соответственно. Применим метод индукции и последовательно решим в символьной форме поставленную задачу для фермы с 1, 2, 3 и т. д. панелями. Для каждого варианта определим прогиб при нагрузке, приложенной поочередно в каждый узел нижнего пояса. Сначала найдем последовательности целочисленных коэффициентов перед соответствующими выражениями, а затем и их общие члены при 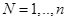 и
и  , где
, где  номер нагруженного узла. Однородные рекуррентные уравнения получены с помощью оператора rgf_findrecur, входящего в состав пакета genfunc системы компьютерной математики Maple [6, 7]. Решение уравнения дает оператор rsolve. Имея аналитические выражения для прогибов во всех стержнях статически определимой фермы, можно определить прогиб фермы как функцию ее геометрических параметров, числа панелей и номера узла, к которому приложена нагрузка.
номер нагруженного узла. Однородные рекуррентные уравнения получены с помощью оператора rgf_findrecur, входящего в состав пакета genfunc системы компьютерной математики Maple [6, 7]. Решение уравнения дает оператор rsolve. Имея аналитические выражения для прогибов во всех стержнях статически определимой фермы, можно определить прогиб фермы как функцию ее геометрических параметров, числа панелей и номера узла, к которому приложена нагрузка.
 панелей; нижнего пояса, включающего в себя
панелей; нижнего пояса, включающего в себя  горизонтальных стержней длиной
горизонтальных стержней длиной  и раскосов из
и раскосов из  вертикальных стержней длиной
вертикальных стержней длиной  стержней, включая три опорных, моделирующих шарнирные опоры, и
стержней, включая три опорных, моделирующих шарнирные опоры, и  узлов, дающих
узлов, дающих  уравнений равновесия.
уравнений равновесия. половина длины одной панели,
половина длины одной панели,  высота панели):
высота панели):


 ,
,  , координатами которых являются номера шарниров по их концам. Шарнирные опоры смоделируем в виде двух стержней в неподвижной шарнирной опоре и одного вертикального в подвижной. Отметим, что направления этих векторов просто определяют структуру соединений стержней в ферме и никак не связаны со знаками усилий в стержнях.
, координатами которых являются номера шарниров по их концам. Шарнирные опоры смоделируем в виде двух стержней в неподвижной шарнирной опоре и одного вертикального в подвижной. Отметим, что направления этих векторов просто определяют структуру соединений стержней в ферме и никак не связаны со знаками усилий в стержнях.



 .
.
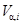 означает номер компоненты вектора
означает номер компоненты вектора 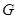 имеет следующие элементы:
имеет следующие элементы:

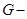 матрица направляющих косинусов,
матрица направляющих косинусов,  вспомогательная переменная, приводящая к тому, что усилия опорных стержней появляются в уравнениях только один раз. Решив систему (1) для вертикальной единичной силы, приложенной поочередно к каждому узлу нижнего пояса, получим выражения следующего вида:
вспомогательная переменная, приводящая к тому, что усилия опорных стержней появляются в уравнениях только один раз. Решив систему (1) для вертикальной единичной силы, приложенной поочередно к каждому узлу нижнего пояса, получим выражения следующего вида:
 величина нагрузки,
величина нагрузки,  элементы массива, содержащего коэффициенты перед соответствующими геометрическими параметрами для каждого вычисления,
элементы массива, содержащего коэффициенты перед соответствующими геометрическими параметрами для каждого вычисления,  число панелей, при котором получено это значение. Стоит отметить данный тип ферм имеет разную структуру при четном и нечетном n, а именно отличается форма центрального узла. Как следствие, при нагружении в «центре» коэффициент перед
число панелей, при котором получено это значение. Стоит отметить данный тип ферм имеет разную структуру при четном и нечетном n, а именно отличается форма центрального узла. Как следствие, при нагружении в «центре» коэффициент перед 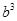 при четном числе панелей принимает значение равное трем, в остальных случаях равен единице.
при четном числе панелей принимает значение равное трем, в остальных случаях равен единице.


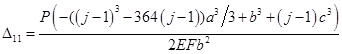

 .
.
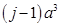 : 244 364 508….2188. Выписав последовательность этих коэффициентов, и найдя для них рекуррентное уравнение при помощи операторов rgf_findrecur, rsolve, получена формула (14):
: 244 364 508….2188. Выписав последовательность этих коэффициентов, и найдя для них рекуррентное уравнение при помощи операторов rgf_findrecur, rsolve, получена формула (14):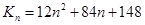 ,
,
 выражение, удовлетворяющее коэффициенту при j в
выражение, удовлетворяющее коэффициенту при j в  к
к  , от
, от 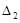 к
к  и т. д. соответственно. Для этого сделаем замену
и т. д. соответственно. Для этого сделаем замену  .
. .
.
 .
.
 .
.
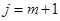 , т. к. это значение соответствует центральному узлу, то получится выражение, отличное от (17) только коэффициентом при b.
, т. к. это значение соответствует центральному узлу, то получится выражение, отличное от (17) только коэффициентом при b.



