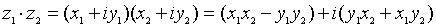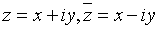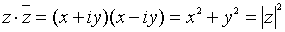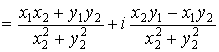Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Составить Закон распределения числа попаданий в цель при четырех выстрелах, если вероятность попадания при одном выстреле равна 0,9.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Решение. Случайная величина Х – число попаданий в цель при четырех выстрелах – может принимать значения 0,1,2,3,4, а соответствующие им вероятности находим по формуле Бернулли:
Итак, искомый закон распределения имеет вид (табл.8): Таблица 8 - Закон распределения числа попаданий в цель при четырех выстрелах
Математическое ожидание. Среди числовых характеристик ДСВ весьма важной является математическое ожидание, которое указывает, какое среднее значение случайной величины следует ожидать в результате испытаний или наблюдений. Математическим ожиданием М(Х) дискретной случайной величины Х называется сумма произведений всех ее возможных значений на их вероятности: M(X)= Пример. Найти математическое ожидание случайной величины Х, зная закон распределения (табл.9):
Таблица 9 - Закон распределения ДСВ По формуле находим М(Х)=-1∙0,2+0∙0,1+1∙0,25+2∙0,15+3∙0,3=1,25 Дисперсия. Дисперсией ДСВ называется математическое ожидание квадрата ее отклонения: D(X)=M(X-M(X))2 (18) Более удобной для вычисления является формула: D(X)=М(Х2) – (М(Х))2 (19) Пример. Дискретная случайная величина распределена по закону (табл.10): Таблица 10 - Закон распределения ДСВ
Найти D(X). Находим сначала М(Х)=-1∙0,2+0∙0,1+1∙0,3+2∙0,4=0,9, а затем М(Х2)=1∙0,2=0∙0,1+1∙0,3+4∙0,4=2,1. D(X)=2,1-0,92=2,1-0,81=1,29 Среднее квадратическое отклонение ДСВ. Средним квадратическим отклонением случайной величины Х называется квадратный корень из дисперсии. σ(Х)= Раздел 6. Основы теории комплексных чисел Определение комплексного числа в алгебраической форме, действия с комплексными числами Во множестве действительных чисел нельзя решить уравнение Алгебраическая форма комплексного числа Определение. Комплексным числом называется число Пример. Определение. Модулем комплексного числа Определение. Аргументом комплексного числа Пример. Определение. Два комплексных числа Определение. Комплексное число Определение. Число Пример. Сложение и умножение комплексных чисел производится по правилам сложения и умножения алгебраических многочленов; учитывая при этом, что Пусть Замечание.
|
||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-02-07; просмотров: 8924; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 52.15.57.186 (0.005 с.) |


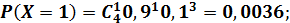
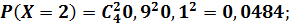
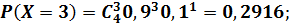
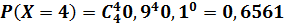
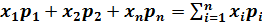 (17)
(17)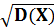 (20)
(20) . Расширяя действительные числа, введем число
. Расширяя действительные числа, введем число 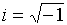 - мнимая единица:
- мнимая единица:  . Тогда, уравнение будет иметь решение
. Тогда, уравнение будет иметь решение  .
. , где x -называется действительной частью комплексного числа и обозначается
, где x -называется действительной частью комплексного числа и обозначается  ;
;  называется мнимой частью комплексного числа и обозначается
называется мнимой частью комплексного числа и обозначается 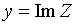 . Такая запись комплексного числа называется алгебраической формой комплексного числа.
. Такая запись комплексного числа называется алгебраической формой комплексного числа.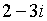 .
. 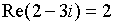 ,
,  .
.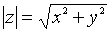 .
.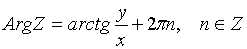 . Главное значение аргумента обозначается: arg z=
. Главное значение аргумента обозначается: arg z= 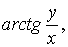
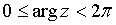 или
или  .
.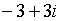



 ,
,  называются равными
называются равными 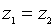 , если
, если  ,
,  .
.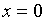 и
и 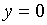 .
.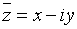 называется сопряженным комплексному числу
называется сопряженным комплексному числу 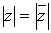 .
.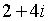 ;
; 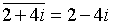 .
.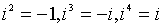 и т.д.
и т.д.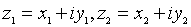
 .
.