Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Понятие производной. Правила и формулы дифференцирования. Производная сложной функцииСодержание книги
Поиск на нашем сайте
Рассмотрим задачу: Точка движется по параболе неравномерно. Дана парабола Решение:
Найдем среднюю скорость движения точки на первом промежутке. Рассмотрим рисунок 1. Здесь
 , получим , получим 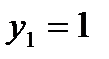 и и  . Тогда . Тогда  . .
Аналогично при
Рисунок1 - Движение точки по параболе Чем меньше промежуток, тем точнее средняя скорость выражает действительную скорость движения точки по параболе. Значение скорости движения точки в общем виде выражают формулой: Создатели: Лейбниц, Ньютон, Эйлер. Определение: Производной функции называется предел отношения приращения функции к приращению аргумента, когда приращение аргумента стремится к нулю
Дифференцирование – это операция нахождения производной функции.
Пример: Найти производную функции Решение: Будем искать производную по определению
Получаем следующее выражение:
Дифференцирование состоит из двух этапов: ¾ применение правил дифференцирования; ¾ применение формул дифференцирования.
Правила и формулы дифференцирования.
С – const; u, v – функции 1. 2. 3. 4. Таблица 1 - Таблица производных
Примеры: 1) Применяем правило: 2) Применяем правило: 3) Применяем правило: 4) Применяем правило: 5) Применяем правило: Аналогично: 6) 7) По формуле Аналогично: 8) 9) 10) По правилу 11) Применяем правило:
12) Применяем правило:
Решите самостоятельно: а) б) Производная сложной функции Пусть дана сложная функция y=g(u), где u=f(x). Теорема 1. Если функция u=f(x) дифференцируема в некоторой точке x, а функция y=g(u) определена на множестве значений функции f(x) и дифференцируема в точке u=f(x), то сложная функция y=g(f(x)) в данной точке x имеет производную, которая находится по формуле
Примеры: 1) Найти производную функции
Данная функция является сложной степенной функцией y= u9, где u =
2) Найти производную функции
Эта функция также является сложной степенной функцией, а именно
Применение производной к исследованию функций и построению графиков
|
||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-02-07; просмотров: 274; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.137.164.139 (0.007 с.) |

 - средняя скорость движения точки на указанном промежутке.
- средняя скорость движения точки на указанном промежутке. и
и  . Подставив
. Подставив и
и  находим
находим  и
и  . Тогда
. Тогда 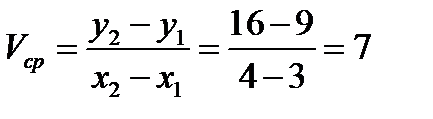 .
.
 - производная функции
- производная функции  .
.
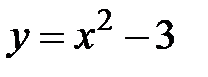 по определению.
по определению.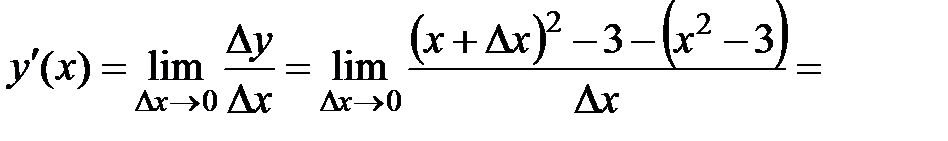

 .
.
 –для конечного числа слагаемых
–для конечного числа слагаемых




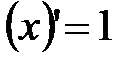
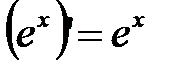

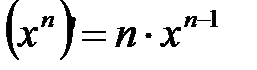 ;
;










 , получим:
, получим:  , т.к.
, т.к.  ;
;
 , т.к.
, т.к.  ;
;
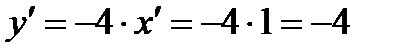 , т.к.
, т.к. 
 , получим:
, получим:  , т.к.
, т.к. 
 , т.к.
, т.к.  , получим:
, получим:  ;
;
 , получим:
, получим:  ;
; , получим:
, получим:  ;
; , получим:
, получим: 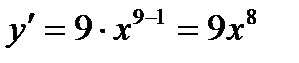 ;
;
 , получим:
, получим:  ;
;

 ;
;

 ;
; ;
; (по правилу умножения и по правилу частного)
(по правилу умножения и по правилу частного) или
или  (3)
(3)
 . Поэтому получим:
. Поэтому получим:

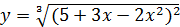
 , где u=
, где u=  . Поэтому
. Поэтому