
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Основные операции над множествамиСодержание книги
Поиск на нашем сайте
1. Включение Множество А входит (включено) в множество В, или А является подмножеством В. Если всякий объект, обладающий свойством 2. Объединение Сумма множеств А и В есть множество С, включающее в себя все элементы множество А и В. Объект входит во множество
3. Пересечение Пересечением множество А и В называется новое множество С. Элементы множества С принадлежат множеству А (обладают его свойствами) и множеству В (обладают его свойствами).
4. Разность Разность множеств А и В есть множество С, элементы которого обладают свойствами множества А и не обладают свойствами множества В или принадлежат множеству А и не принадлежат множеству В.
5. Дополнение Если имеется некоторое универсальное множество (универсум) U и все рассматриваемые множества есть его подмножества, то дополнением
Таблица 4 - Связь между логическими операциями и операциями над множествами.
Будем называть вектором (кортежем) упорядоченный набор элементов и обозначать его Количество элементов в векторе называется его длиной, если в векторе 2 элемента, то - пара, если n элементов, то - n-ка. 5. (Диаграммы Эйлера - Венна)
Рисунок 10 -
Рисунок 11 -
Рисунок 12 -
Рисунок 13 - Декартово произведение (прямое) множеств А1,А2,…Ап назыв. множество А1×А2×…Ап, состоящее из всех кортежей Например, декартовым произведением множеств А= Раздел 5. Основы теории вероятностей и математической статистики
Элементы комбинаторики: размещения, перестановки, Сочетания Основная задача комбинаторики – пересчет и перечисление элементов в конечных множествах. Если нас интересует, сколько элементов принадлежащих данному конечному множеству обладают некоторым свойством, то это задача пересчета. Если необходимо выделить все элементы множества, обладающие заданными свойствами, то это задача перечисления. Рассмотрим следующие элементы комбинаторики, позволяющие решать вышеупомянутые задачи. К таким объектам относятся: 1. перестановки (с повторением и без них); 2. размещения (с повторением и без них); 3. сочетания (с повторением и без них); Перестановками называют комбинации, состоящие из одних и тех же элементов и отличающиеся только порядком их расположения. Число всех возможных перестановок обозначается
Перестановки с повторениями вычисляются по формуле:
где Пример 39. Определим, сколько различных слов можно составить из слова «литература». В слове «литература» п1 =1 буква «л», п2 =1 буква «и», п3 =2 буквы «т», п4 =1 буква «е», п5 =2 буквы «р», п6 =2 буквы «а», п7 =1 буква «у».
Тогда из слова «литература» можно составить Р(п1,п2,п3,п4,п5,п6,п7)= Сочетанием называются такие комбинации элементов, которые отличаются между собой в каждой группе только самими элементами (но не порядком их расположения в группе).
Пример 40. В почтовом отделении продаются открытки п =5 видов. Определим число способов покупки т =7 открыток. Число способов покупки открыток равно числу сочетаний с повторениями из п =5 элементов по т =7 элементов и равно Размещением называются такие комбинации элементов, которые отличаются между собой или самими элементами или порядком их расположения в группе.
Пример 41. Определим, сколько четырехзначных чисел можно составить из цифр 3,5,6,7,8. Составление четырехзначных чисел из пяти цифр – размещение из п =5 элементов по т =4 элемента с повторениями. Тогда всего можно составить
|
||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-02-07; просмотров: 267; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.191.70.200 (0.007 с.) |

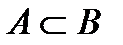
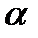 , также обладает свойством
, также обладает свойством 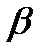 , то говорят, что свойство
, то говорят, что свойство 
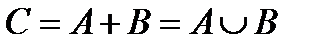 если он входит во множество А или во множество В.
если он входит во множество А или во множество В.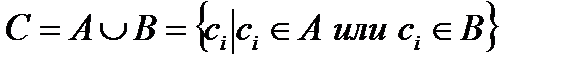
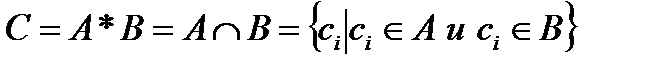
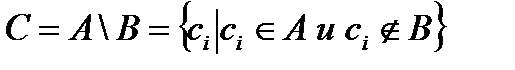
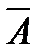 называется такое множество, элементы которого не входят в А, но принадлежат U.
называется такое множество, элементы которого не входят в А, но принадлежат U.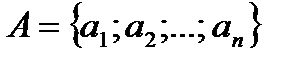 , заметим, что в отличие от множества, элементы в векторе могут повторяться. Эти элементы называются координатами или проекциями.
, заметим, что в отличие от множества, элементы в векторе могут повторяться. Эти элементы называются координатами или проекциями.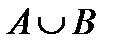
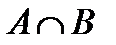
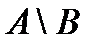
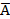
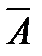
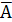
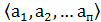 длины к.
длины к.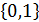 и В=
и В= 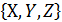 будет являться множество пар А×В =
будет являться множество пар А×В = 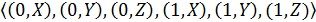
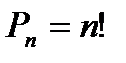 (без повторений) (9)
(без повторений) (9)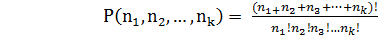 (10)
(10)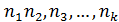 - число повторений элементов каждого вида.
- число повторений элементов каждого вида.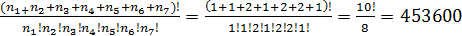 различных слов.
различных слов.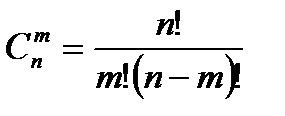 (без повторения) (11)
(без повторения) (11)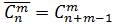 (с повторением) (12)
(с повторением) (12)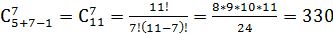 .
.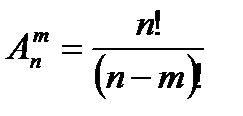 (без повторения) (13)
(без повторения) (13)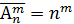 (с повторением) (14)
(с повторением) (14)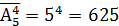 чисел.
чисел.


