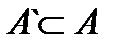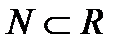Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Приложения определенного интеграла к вычислению площадей плоских фигурСодержание книги
Поиск на нашем сайте
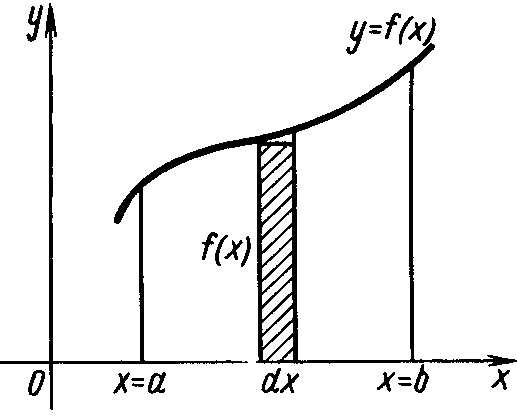
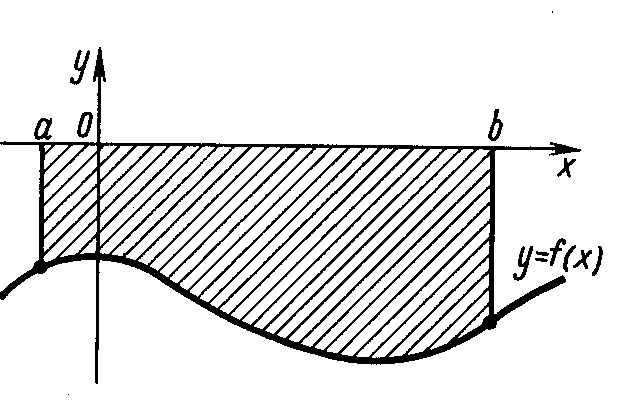
Найдем площадь S криволинейной трапеции, ограниченной кривой y=f(x), осью Ох и двумя прямыми х = а и х = в, где а≤ х≤ в, f(x)≥0 (рис.5)
Рисунок 5 - Криволинейная трапеция Так как дифференциал переменной площади S есть площадь прямоугольника с основанием dx и высотой f(x), т.е. dS=f(x)dx, то, интегрируя это равенство в пределах от а до в, получим
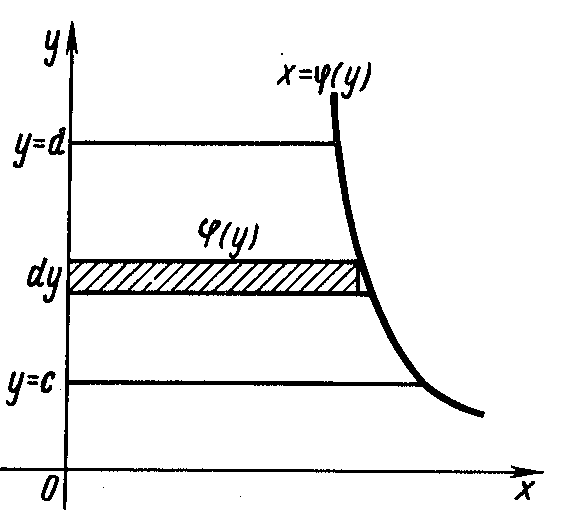
Если криволинейная трапеция прилегает к оси Oy так, что c≤y≤d, x=φ(y)≥0 (рис.6),
Рисунок 6 - Криволинейная трапеция прилегает к оси Oy то дифференциал переменной площади S равен dS=f(y)dy, откуда
В том случае, когда криволинейная трапеция, ограниченная кривой y=f(x), осью Ох и прямыми х = а и х = в, лежит под осью Ох (рис.7),
Рисунок 7 - Криволинейная трапеция лежит под осью Ох площадь находится по формуле
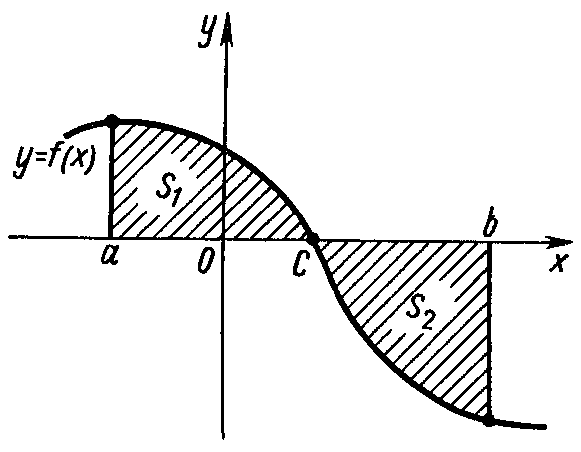
Если фигура, ограниченная кривой y=f(x), осью Ох и прямыми х = а и х = в, расположена по обе стороны от оси Ох (рис.8),
Рисунок 8 - Криволинейная трапеция расположена по обе стороны от оси Ох то
Пусть, наконец, фигура
Рисунок 9 - Фигура Тогда ее площадь находится по формуле
Раздел 4. Основы дискретной математики
Множества. Операции над множествами. Бинарные Отношения Множество – совокупность элементов, обладающих каким-то одним общим свойством. Предметы, составляющие множество, называются его элементами. Говорят, что они принадлежат множеству. Символически это записывается так: а∈А. Множества будем обозначать загл. буквами (А,В,С), а элементы – маленькими (а,в,с). Запись а∉А означает, что элемент а не принадлежит множеству А. Пример 1. Пусть А – множество делителей числа 12. Тогда 2 ∈А, а 5 ∉А. Если каждому элементу множества можно присвоить номер и этот номер не повторяется, то такое множество называется счетным или конечным. Если такого номера для каждого элемента не существует, то такое множество называется бесконечным. Бесконечное множество часто называют континуумом (например: совокупность точек на плоскости). Если можно пересчитать все число элементов в счетном множестве, то эта сумма называется мощностью множества. 2. Множества можно задать следующим образом. · Перечислением всех входящих в него объектов. · Описанием свойств, которыми должны обладать элементы множества. Например, множество четных чисел, меньших 10, можно задать в след. виде: М= Любую часть множества А, выбранную по определенному признаку, называют подмножеством, и обычно обозначают буквой со штрихом, т.е.
Множество, не содержащее ни одного элемента, называют пустым и обозначают ∅. Свойства счетных множеств 1. Всякое подмножество счетного множества конечно или счетно Подмножеством множества А называется множество А` все элементы которого принадлежат множеству А
Пример: 2. Сумма конечного или счетного числа конечных или счетных множеств есть конечное или счетное множество. 3. Множество всех рациональных чисел счетно. 4. Алфавитом называется любое непустое множество. Элементы множества под названием АЛФАВИТ называют буквами (символами). Символом в данном алфавите любая конечная последовательность букв. Для каждого множества А существуют множества, элементами которого являются только все его подмножества. Такое подмножество называют семейством множеств А или булеаном. (обозначается В(А))
|
||||
|
Последнее изменение этой страницы: 2017-02-07; просмотров: 362; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.21.100.34 (0.007 с.) |

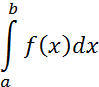
 (5)
(5)
 (6)
(6)
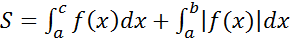 (7)
(7) ограничена двумя пересекающимися кривыми y=f1(x) и y=f2(x) и прямыми х = а и х = в, где a≤x≤b и f1(x)≤ f2(x) (рис.9).
ограничена двумя пересекающимися кривыми y=f1(x) и y=f2(x) и прямыми х = а и х = в, где a≤x≤b и f1(x)≤ f2(x) (рис.9).
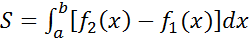 (8)
(8)
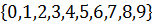 - множество десятичных цифр.
- множество десятичных цифр. или
или  , причем справа от наклонной черты указано свойство элементов этого множества. Этот способ называется аналитическим.
, причем справа от наклонной черты указано свойство элементов этого множества. Этот способ называется аналитическим. :
: , где ⊂ - символ включения.
, где ⊂ - символ включения.