
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Уравнение прямой, проходящей через 2 заданные точки в пространстве. Параметрическое уравнение прямой. Нахождение точки пересечения прямой и плоскости.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте Чтобы точка M лежала на прямой L, вектор M1M должен быть параллелен вектору q. Условие параллельности векторов состоит в пропорциональности сходственных координат, из чего следует
Уравнение прямой, проходящей через две заданные точкиM1(x1,y1,z1) и M2(x2,y2,z2) получим из уравнения (1), приняв, что направляющий вектор
и подставив выражение (2) в (1):
Приравняв выражение (1) параметру t, получим параметрические уравнения прямой.
Эти уравнения имеют наглядное физическое истолкование. Если принять что, t −время, а Найти точку пересечения прямой:
и плоскости:
Решение. Приравняем выражение (1) к параметру t и выразим через него x, y и z
Подставим x, y и z из (4) в уравнение плоскости.
Координаты точки пересечения прямой и плоскости получим, подставив значение t0, найденное из (5) в уравнения (4).
Угол между прямыми в пространстве. Угол между прямой и плоскостью. Угол между прямыми очевидным образом связан с соответствующими соотношениями между направляющими векторами q этих прямых.
Угол между плоскостью
И прямой
Определяется как дополнительный к углу между нормальным вектором плоскости
Условие принадлежности 2-х прямых одной плоскости. Условие принадлежности прямой заданной плоскости. Для того, чтобы две прямые (1) и (2) принадлежали
одной плоскости необходимо и достаточно, чтобы три вектора
были компланарны. Где M1 и M2 – точки принадлежащие плоскости. Приравняв нулю смешанное произведение этих векторов, получим условие принадлежности двух прямых к одной плоскости.
Плоскость
Прямая
Для того, чтобы прямая (2) принадлежала плоскости (1) должны быть выполнены два условия: 3. условие параллельности прямой и плоскости
4. координаты точки M1(x1,y1,z1), принадлежащей прямой, должны обращать уравнение плоскости в тождество
29) Задача о плоскости П проходящей через прямую L1 параллельно прямой L2 Составить уравнение плоскости, проходящей через одну из скрещивающихся прямых параллельно второй.
Решение. Ориентацию в пространстве искомой плоскости определяют направляющие вектора прямых
Введем в рассмотрение «свободный вектор»
конечная точка которого M(x,y,z) −.произвольная точка пространства, а начальная точка M1(x1,y1,z1) взята с первой прямой. Из условия компланарности рассматриваемых векторов запишем уравнение искомой плоскости в матричной форме.
30) Задача о прямой L2 проходящей через точку M0? Перпендикулярно прямой L1 (L1 и L2 пересекаются) Дана прямая Составить уравнение прямой, походящей через данную точку перпендикулярно заданной прямой. Решение. Нормальный вектор прямой Чтобы «свободная точка» - M (x,y) принадлежала искомой прямой, вектор
есть искомое уравнение в каноническом виде. Умножив (2) на произведение
Условия A1=0 или B1=0 означают, что соответствующие числители обращаются в нуль. Заметим, что в случае перпендикулярности прямых коэффициенты при переменных x и y меняются местами, а у одного из них меняется знак. 31) Система трех линейных уравнений с тремя неизвестными. Теорема Крамера (доказательство для системы двух уравнений) Случаи
|
||
|
Последнее изменение этой страницы: 2017-01-26; просмотров: 1473; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.2 (0.008 с.) |

 (1)
(1) (2)
(2)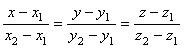 (3)
(3) (4)
(4) вектор скорости, то уравнения (4) − это три проекции уравнения движения точки на координатные оси.
вектор скорости, то уравнения (4) − это три проекции уравнения движения точки на координатные оси. (1)
(1) (2)
(2) (3)
(3) (4)
(4) (5)
(5) (6)
(6) . (1)
. (1) (1)
(1) (2)
(2) и направляющим вектором прямой
и направляющим вектором прямой  . Если угол между векторами обозначить
. Если угол между векторами обозначить  , а угол меду прямой и плоскостью
, а угол меду прямой и плоскостью 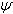 , то
, то  . Следовательно:
. Следовательно: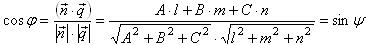 . (3)
. (3)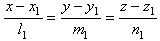 (1)
(1) (2)
(2) и
и
 (3)
(3) (1)
(1) (2)
(2) (3)
(3) (4)
(4) (1)
(1)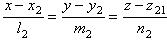 (2)
(2) и
и 
 ,
, . (3)
. (3) . (1)
. (1) будет направляющим вектором для искомой прямой.
будет направляющим вектором для искомой прямой. должен быть параллелен вектору n1. Условие параллельности векторов:
должен быть параллелен вектору n1. Условие параллельности векторов: (2)
(2) и введя обозначение
и введя обозначение  запишем искомое уравнение в общем виде
запишем искомое уравнение в общем виде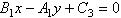 . (3)
. (3) =0,
=0,  . Геометрическая интерпритация.
. Геометрическая интерпритация.


