
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Числовая ось. Прямоугольные декартовы координаты на плоскости и в пространстве. Координаты точки. Направленный отрезок и его проекции на оси координат.Стр 1 из 7Следующая ⇒
Свойства проекций вектора Проекция вектора
Проекция суммы двух векторов на ось равна сумме проекций векторов на ту же ось: Если вектор
Каноническое уравнение прямой на плоскости. Параметрическое уравнение прямой. Уравнение прямой, проходящей через 2 заданные точки. Уравнение прямой с угловым коэффициентом. Каждый не равный нулю вектор, лежащий на данной прямой или параллельный ей, называется направляющим вектором этой прямой. Координаты направляющего вектора l, m, n: a = {l;m;n}. Если известна одна точка M0 (x0;y0;z0) прямой и направляющий вектор a = {l;m;n}, то прямая может быть определена (двумя) уравнениями вида:
Канонические уравнения прямой, проходящей через данные точки M1 (x1;y1;z1) и M2 (x2;y2;z2), имеют вид
Это параметрические уравнения прямой, проходящей через точку M0 (x0;y0;z0) в направлении вектора a = {l;m;n}. В уравнениях (3) t рассматривается как произвольно имеющийся параметр, x,y,z – как функции от t; при изменении t величины x,y,z меняются так, что M (x;y;z) движется по данной прямой. Если параметр t рассматривать как переменное время, а уравнения (3) как уравнения движения точки M, то эти уравнения будут определять прямолинейное и равномерное движение точки M. При t = 0 M совпадает с точкой M0. Скорость v точки M и определяется формулой:
V= к = tg
Уравнение y = kx + b называется уравнением прямой с угловым коэффициентом; k – угловой коэффициент, b – величина отрезка, который отсекает прямая на оси Оу. Считая от начала координат. Если прямая задана общим уравнением Ах+Ву+С=0, то ее угловой коэффициент определяется по формуле: K = - Умножив выражение
Если принять обозначение
Здесь
Угол между плоскостью
И прямой
Определяется как дополнительный к углу между нормальным вектором плоскости Если угол между векторами обозначить
Условие перпендикулярности векторов
соответствует параллельности прямой и плоскости, а условие парллельности векторов
означает перпендикулярность прямой и плоскости.
Для того, чтобы прямая (7.16) принадлежала плоскости (7.15) должны быть выполнены два условия: 1. условие параллельности прямой и плоскости
2. координаты точки
Для того, чтобы две прямые (7.22) и (7.23) принадлежали
одной плоскости необходимо и достаточно, чтобы три вектора
были компланарны.
Приравняв нулю смешанное произведение этих векторов, получим условие принадлежности двух прямых к одной плоскости. ______________________________________________________________ Условие параллельности двух прямых на плоскости: Прямые A1x + B1y + C1 = 0 и A2x + B2y + C2 = 0 являются параллельными тогда и только тогда, когда
Условие перпендикулярности двух прямых на плоскости: Прямые A1x + B1y + C1 = 0 и A2x + B2y + C2 = 0 являются перпендикулярными тогда и только тогда, когда A1A2 + B1B2 = 0
Каноническое уравнение прямой в пространстве:
Общее уравнение прямой линии на плоскости в декартовых координатах: Ax + By + C = 0
Типовые задачи. Задача 6.2. Дана плоскость Составить уравнение плоскости, походящей через данную точку параллельно заданной плоскости. Решение. Нормальный вектор заданной плоскости Чтобы «свободная точка»
есть искомое уравнение. Раскрыв скобки и введя обозначение
Задача 6.3. Задано уравнение пучка плоскостей
и плоскость
Составить уравнение плоскости, принадлежащей пучку, параллельной плоскости Решение. Преобразуем уравнение (6.26)
Это уравнение искомой плоскости. Его нормальный вектор, имеющий вид
параллелен вектору Условие параллельности векторов
содержит единственную неизвестную величину
Угол между плоскостью
И прямой
Определяется как дополнительный к углу между нормальным вектором плоскости
Плоскость
Прямая
Для того, чтобы прямая (2) принадлежала плоскости (1) должны быть выполнены два условия: 3. условие параллельности прямой и плоскости
4. координаты точки M1(x1,y1,z1), принадлежащей прямой, должны обращать уравнение плоскости в тождество
29) Задача о плоскости П проходящей через прямую L1 параллельно прямой L2 Составить уравнение плоскости, проходящей через одну из скрещивающихся прямых параллельно второй.
Решение. Ориентацию в пространстве искомой плоскости определяют направляющие вектора прямых
Введем в рассмотрение «свободный вектор»
конечная точка которого M(x,y,z) −.произвольная точка пространства, а начальная точка M1(x1,y1,z1) взята с первой прямой. Из условия компланарности рассматриваемых векторов запишем уравнение искомой плоскости в матричной форме.
30) Задача о прямой L2 проходящей через точку M0? Перпендикулярно прямой L1 (L1 и L2 пересекаются) Дана прямая Составить уравнение прямой, походящей через данную точку перпендикулярно заданной прямой. Решение. Нормальный вектор прямой Чтобы «свободная точка» - M (x,y) принадлежала искомой прямой, вектор
есть искомое уравнение в каноническом виде. Умножив (2) на произведение
Условия A1=0 или B1=0 означают, что соответствующие числители обращаются в нуль. Заметим, что в случае перпендикулярности прямых коэффициенты при переменных x и y меняются местами, а у одного из них меняется знак. 31) Система трех линейных уравнений с тремя неизвестными. Теорема Крамера (доказательство для системы двух уравнений) Случаи Числовая ось. Прямоугольные Декартовы координаты на плоскости и в пространстве. Координаты точки. Направленный отрезок и его проекции на оси координат. Числовая ось, или числовая прямая — это бесконечная прямая, на которой выбраны: некоторая точка O — начало отсчета; положительное направление, указанное стрелкой; масштаб для измерения длин. Декартовы координаты на плоскости образуют две взаимно перпендикулярные оси с общим началом отсчета и общей масштабной единицей. Ось
Рис.1 Декартовыми прямоугольными координатами
Оси координат разбивают плоскость на четыре квадранта. В первом квадранте
Декартовы координаты в пространстве вводятся аналогично декартовым координатам на плоскости. Три взаимно перпендикулярные координатные оси с общим началом Система координат называется правой, если из конца оси Декартовыми прямоугольными координатами Через каждую пару осей можно провести координатные плоскости
Рис.2
Координаты точки. Пусть дана произвольная прямая A. Выберем некоторый отрезок в качестве единицы измерения длин, назначим на прямой А положительное направление(после чего она становится осью) и отметим на этой прямой буквой О какую-нибудь точку. Тем самым на прямой А будет введена система координат. Координатой любой точки М прямой А (в установленной системе координат) называется число х, равное величине отрезка ОМ: х=ОМ. Точка О – начало координат.
Рис.3
Отрезок Проекцией отрезка АВ на ось и называется число, равное величине отрезка А1В1 оси и , где точка А1 является проекцией точки А на ось и, а В1 – проекцией точки В на эту же ось. Проекция отрезка АВ на ось и обозначается символом ПР и АВ.
2. Матрица и определитель третьего порядка. Свойства определителей. Вычисление детерминанта. Прямоугольная таблица из чисел, содержащая Определителем третьего порядка
Свойство 1. Величина определителя не изменится, если строки и столбцы определителя поменять местами, т.е.
Свойство 2. Перестановка двух строк (или двух столбцов) определителя равносильна умножению его на число Свойство 3. Если определитель имеет две одинаковые сроки (или два одинаковых столбца), то он равен нулю. Свойство 4. Умножение всех элементов некоторой строки (или некоторого столбца) определителя на число Свойство 5. Ели все элементы некоторой строки (или столбца) определителя равны нулю, то и сам определитель равен нулю. Свойство 6. Если элементы двух строк (или двух столбцов) определителя пропорциональны, то определитель равен нулю. Свойство 7. Если каждый элемент к-го столбца определителя является суммой двух слагаемых, то определитель может быть представлен в виде суммы двух определителей, первый из которых в к-ом столбце содержит первые слагаемые упомянутых сумм, а в к-ом столбце второго стоят вторые слагаемые, остальные же столбцы определителей совпадают со столбцами исходного определителя. Аналогичное утверждение справедливо для строк определителя. Например,
Вычисление определителя третьего порядка: 1. Способ 2. Способ
3. Определитель третьего порядка. Алгебраические дополнения и миноры. Разложение определителя по элементам строки или столбца.
Выражения в скобках будем называть алгебраическими дополнениями элементов первой строки определителя и обозначать большими буквами с теми же индексами. Выражение называется разложением определителя по элементам первой стоки. Минором данного элемента определителя
4. Вектор. Разложение вектора по базису i,j,k. Длина вектора, сложение, вычитание, умножение на число. Отрезок Определение. Т ри линейно независимыхвектора Определение. Суммой Для операции сложения векторов справедливы четыре аксиомы: 1) 2) 3) Существует нулевой вектор 4) Для каждого вектора Определение. Разностью Определение. Произведением
5. Направляющие cos, орт вектора. Линейные свойства проекций вектора. Вектор единичной длины называется ортом и обозначается символом Очевидно что, Разложение орта по базису
В соответствии теоремой Пифагора для трехмерного случая
а также
Принято называть
Свойства проекций вектора Проекция вектора
Проекция суммы двух векторов на ось равна сумме проекций векторов на ту же ось: Если вектор
|
|||||||||
|
Последнее изменение этой страницы: 2017-01-26; просмотров: 289; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.186.6 (0.115 с.) |
 на ось l равна произведению модуля вектора
на ось l равна произведению модуля вектора 
 .
.
 .
. (1) В таком виде уравнения прямой называются каноническими.
(1) В таком виде уравнения прямой называются каноническими. (2) Обозначим буквой t каждое из равных отношений в канонических уравнениях (1); получим:
(2) Обозначим буквой t каждое из равных отношений в канонических уравнениях (1); получим: Уравнение
Уравнение  является уравнением прямой, проходящей через две точки M1(x1;y1) и M2 (x2;y2). Угол
является уравнением прямой, проходящей через две точки M1(x1;y1) и M2 (x2;y2). Угол  , называется углом наклона прямой к оси Ох. Тангенс угла наклона прямой к оси Ох называется угловым коэффициентом прямой; его обычно обозначают буквой к:
, называется углом наклона прямой к оси Ох. Тангенс угла наклона прямой к оси Ох называется угловым коэффициентом прямой; его обычно обозначают буквой к:

 .
. на число
на число  и подставив в него
и подставив в него  , получим:
, получим: (5.12)
(5.12) , уравнение примет следующий вид:
, уравнение примет следующий вид: . (5.13)
. (5.13) координата точки пересечения прямой
координата точки пересечения прямой  с осью
с осью  , в чем легко убедиться, подставив в (5.13) уравнение оси
, в чем легко убедиться, подставив в (5.13) уравнение оси  .
. (7.15)
(7.15) (7.16)
(7.16) и направляющим вектором прямой
и направляющим вектором прямой  .
. , а угол меду прямой и плоскостью
, а угол меду прямой и плоскостью  , то
, то  . Следовательно:
. Следовательно: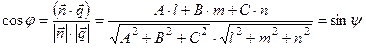 . (7.17)
. (7.17) и
и 
 (7.18)
(7.18)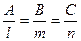 (7.19)
(7.19) (7.20)
(7.20) , принадлежащей прямой, должны обращать уравнение плоскости в тождество
, принадлежащей прямой, должны обращать уравнение плоскости в тождество (7.21)
(7.21) (7.22)
(7.22) (7.23)
(7.23) и
и
 (7.24)
(7.24)
 и точка
и точка  .
. , он же будет нормальным вектором искомой плоскости.
, он же будет нормальным вектором искомой плоскости. принадлежала искомой плоскости, вектор
принадлежала искомой плоскости, вектор  должен быть перпендикулярен вектору
должен быть перпендикулярен вектору  . Условие перпендикулярности векторов
. Условие перпендикулярности векторов (6.24)
(6.24) запишем найденное уравнение в общем виде
запишем найденное уравнение в общем виде (6.25)
(6.25) , (6.26)
, (6.26)
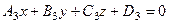 . (6.26*)
. (6.26*)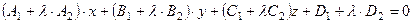 .
. ,
, .
.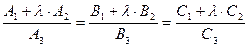 (6.27)
(6.27)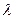 . Определив число
. Определив число  (1)
(1) (2)
(2) и направляющим вектором прямой
и направляющим вектором прямой  . Если угол между векторами обозначить
. Если угол между векторами обозначить  , а угол меду прямой и плоскостью
, а угол меду прямой и плоскостью 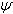 , то
, то  . Следовательно:
. Следовательно: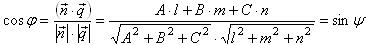 . (3)
. (3) (1)
(1) (2)
(2) (3)
(3) (4)
(4) (1)
(1)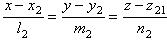 (2)
(2) и
и 
 ,
, . (3)
. (3) . (1)
. (1) будет направляющим вектором для искомой прямой.
будет направляющим вектором для искомой прямой. должен быть параллелен вектору n1. Условие параллельности векторов:
должен быть параллелен вектору n1. Условие параллельности векторов: (2)
(2) и введя обозначение
и введя обозначение  запишем искомое уравнение в общем виде
запишем искомое уравнение в общем виде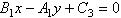 . (3)
. (3) =0,
=0,  . Геометрическая интерпритация.
. Геометрическая интерпритация. называется осью абсцисс ось
называется осью абсцисс ось  на оси
на оси 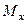 и
и  .
.
 и
и  точки
точки  и
и 
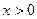 и
и  , во втором
, во втором  ,
,  и одинаковой масштабной единицей образуют декартову прямоугольную систему координат в пространстве. Оси абсцисс и ординат здесь те же самые
и одинаковой масштабной единицей образуют декартову прямоугольную систему координат в пространстве. Оси абсцисс и ординат здесь те же самые 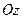 называется осью аппликат.
называется осью аппликат. точки
точки  .
. , которые разбивают пространство на восемь октантов. Нумерация октантов проводится в направлении против часовой стрелки. Первые четыре октанта расположены над плоскостью
, которые разбивают пространство на восемь октантов. Нумерация октантов проводится в направлении против часовой стрелки. Первые четыре октанта расположены над плоскостью  , остальные под ней.
, остальные под ней.

 на оси называется направленным, если указано, какая из его граничных точек является началом, а какая концом.
на оси называется направленным, если указано, какая из его граничных точек является началом, а какая концом. строк и
строк и  называется число, равное алгебраической сумме произведений элементов матрицы, взятых по одному из каждой строки и каждого столбца матрицы
называется число, равное алгебраической сумме произведений элементов матрицы, взятых по одному из каждой строки и каждого столбца матрицы 

 .
.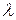 равносильно умножению определителя на это число.
равносильно умножению определителя на это число.




 -го порядка, полученный из данного определителя вычеркиванием сроки и столбца, на пересечении которых стоит элемент и обозначается как
-го порядка, полученный из данного определителя вычеркиванием сроки и столбца, на пересечении которых стоит элемент и обозначается как 
 и
и  образуют базис трехмерного пространства, если любой вектор
образуют базис трехмерного пространства, если любой вектор  может быть представлен линейной комбинацией этих векторов. Любая тройка некомпланарных векторов образует базис трехмерного пространства. Вектор
может быть представлен линейной комбинацией этих векторов. Любая тройка некомпланарных векторов образует базис трехмерного пространства. Вектор  может быть разложен по базису
может быть разложен по базису  , то есть:
, то есть: 
 двух векторов называется вектор
двух векторов называется вектор  , идущий из начала вектора
, идущий из начала вектора  в конец вектора
в конец вектора  , при условии, что начало вектора
, при условии, что начало вектора  (переместительное свойство);
(переместительное свойство); (сочетательное свойство);
(сочетательное свойство);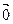 , такой, что
, такой, что  ;
; такой, что
такой, что  .
. двух векторов называется вектор
двух векторов называется вектор 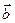 дает вектор
дает вектор  , где
, где  - вектор, противоположный вектору
- вектор, противоположный вектору 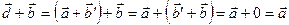 .
. вектора
вектора  , и направление, совпадающее с направлением вектора
, и направление, совпадающее с направлением вектора  и противоположное в случае
и противоположное в случае 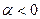 .
. .
.  - это орт вектора
- это орт вектора  , откуда следует, что
, откуда следует, что  (3.1)
(3.1) (3.25)
(3.25) , (3.26)
, (3.26)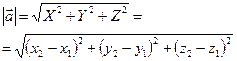 (3.27)
(3.27) и
и  направляющими косинусами вектора
направляющими косинусами вектора  и
и  - углы между вектором и осями
- углы между вектором и осями  и
и  (3.28)
(3.28)



