
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Пучок и связка плоскостей. Уравнение пучка плоскостей. Основные задачи, решаемые с применением уравнения пучка.
Множество плоскостей, пересекающихся по одной прямой Теорема 5.3. Уравнение
есть уравнение пучка плоскостей, если
суть уравнения двух плоскостей, пересекающихся по прямой Доказательство. Преобразуем уравнение к следующему виду:
Это уравнение плоскости, если выражения в скобках не равны нулю одновременно. Предположим противное. Тогда, из
Из Из В итоге Это условие параллельности плоскостей (6.19), что противоречит условиям теоремы. Тем самым доказано, что уравнение (6.18) всегда определяет некоторую плоскость. Покажем, что любая плоскость, принадлежащая пучку определяется уравнением (6.18) при некоторых значениях чисел Подставив координаты точки
В этом уравнении выражения в круглых скобках не могут обратиться в нуль одновременно, так как точка Пусть
Тогда
Из (6.22) значения Можно представить уравнение пучка плоскостей в другом виде, разделив (6.18) на
Связка плоскостей есть множество плоскостей, имеющих одну общую точку
В этом уравнении фиксированы координаты точки Типовые задачи. Задача 6.2. Дана плоскость Составить уравнение плоскости, походящей через данную точку параллельно заданной плоскости. Решение. Нормальный вектор заданной плоскости Чтобы «свободная точка»
есть искомое уравнение. Раскрыв скобки и введя обозначение
Задача 6.3. Задано уравнение пучка плоскостей
и плоскость
Составить уравнение плоскости, принадлежащей пучку, параллельной плоскости Решение. Преобразуем уравнение (6.26)
Это уравнение искомой плоскости. Его нормальный вектор, имеющий вид
параллелен вектору Условие параллельности векторов
содержит единственную неизвестную величину
|
|||||
|
Последнее изменение этой страницы: 2017-01-26; просмотров: 689; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.222.184.162 (0.007 с.) |
 , называется пучком плоскостей
, называется пучком плоскостей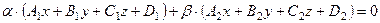 (6.18)
(6.18) и
и  не обращаются в нуль одновременно, а уравнения
не обращаются в нуль одновременно, а уравнения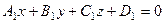 и
и 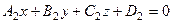 (6.19)
(6.19)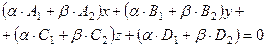 (6.20)
(6.20) следует
следует 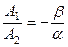 ,
,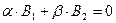 следует
следует  ,
,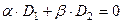 следует
следует  .
.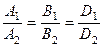 . (6.21)
. (6.21)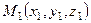 , не принадлежащую прямой
, не принадлежащую прямой  и прямая
и прямая 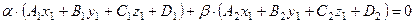
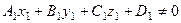 ,
,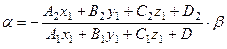 (6.22)
(6.22) :
: (6.23)
(6.23) . Уравнение связки плоскостей имеет вид
. Уравнение связки плоскостей имеет вид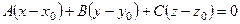 . (6.28)
. (6.28)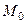 , а коэффициенты
, а коэффициенты 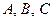 произвольные числа, не обращающиеся в нуль одновременно.
произвольные числа, не обращающиеся в нуль одновременно. и точка
и точка  , он же будет нормальным вектором искомой плоскости.
, он же будет нормальным вектором искомой плоскости. принадлежала искомой плоскости, вектор
принадлежала искомой плоскости, вектор  должен быть перпендикулярен вектору
должен быть перпендикулярен вектору  . Условие перпендикулярности векторов
. Условие перпендикулярности векторов (6.24)
(6.24) запишем найденное уравнение в общем виде
запишем найденное уравнение в общем виде (6.25)
(6.25)
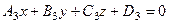 . (6.26*)
. (6.26*)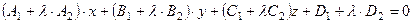 .
. ,
, .
.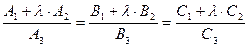 (6.27)
(6.27) . Определив число
. Определив число 


