
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Определение скалярного произведения. Геометрические и алгебраические свойства скалярного произведения.
Скалярным произведением двух векторов называется число, равное произведению длин этих векторов на косинус угла между ними. (Скалярное произведение принято обозначать круглыми скобками.)
Используя представление проекции вектора на другой вектор, можно записать
Скалярное произведение имеет следующие свойства: 1) 2) 3) 4) 5) Эти свойства позволяют при скалярном перемножении векторных многочленов выполнять действия почленно, вынося за скобки числовые множители. Если вектора а и b заданы своими координатами: а = {X1;Y1;Z1}, b = {X2;Y2;Z2}, то их скалярное произведение может быть вычислено по формуле: ab = X1 X2+ Y1 Y2+ Z1 Z2. 7. Вычисление скалярного произведения векторов, заданных компонентами в декартовой системе. Определение. Скалярным произведением двух векторов называется число, равное произведению длин этих векторов на косинус угла между ними. Скалярное произведение имеет следующие свойства: 1) 2) 3) 4) Теорема. Если вектора
Доказательство. Перемножив векторные многочлены a и b, получим:
8. Угол между векторами. Условие ортогональности векторов. Проекция вектора на другой. Угол. Вопрос 7.(для определения скалярного произв. векторов) Теорема. Необходимым и достаточным условием ортогональности двух векторов является равенство нулю их скалярного произведения. Теорема. Проекция вектора Доказательство.
9. Определение векторного произведения векторов. Тройка векторов. Алгебраические и геометрические свойства. Площадь параллелограмма. Определение. Векторным произведением вектора
1) вектор 2) длина вектора 3) упорядоченная тройка векторов Определение. У порядоченная тройка некомпланарных векторов
Это утверждение справедливо для тройки векторов Векторное произведение имеет следующие алгебраические свойства: 1) 2) 3) 4) Теорема. Модуль векторного произведения Доказательство. Поскольку площадь параллелограмма равна произведению длин его смежных сторон на синус угла между ними, доказательство теоремы следует из формулы Теорема 4.5. Если вектора представлены разложениями но базису
10. Векторное произведение векторов, заданных компонентами в декартовых координатах. Условия коллинеарности векторов. Теорема 4.5. Если вектора представлены разложениями но базису
то их векторное произведение имеет вид:
Доказательство. Перемножив векторные многочлены (4.13), получим, что
Строка (4.15) последнего выражения получена с учетом того, что
(Знак минус в этих произведениях получается вследствие нарушения порядка в тройке ортов Очевидно, что выражение (4.15) есть разложение определителя (4.14) по элементам первой строки. Теорема доказана. Теорема 4.3. Необходимым и достаточным условием коллинеарности двух векторов является равенство нулю их векторного произведения. Доказательство. Если
11. Смешанное произведение 3 векторов.Геометрическая интерпретация.Свойства. Условия компланарности 3 векторов. Определение 4.4. Если векторное произведение Теорема 4.6. Смешанное произведение
Доказательство. Тривиальный случай коллинеарности векторов (Знак + берем в случае, если тройка векторов правая). Если же вектора Теорема доказана. Следствие 1. Справедливо равенство
Объём параллелепипеда не зависит от того, какая пара векторов из тройки перемножается векторно. Знак произведения не изменяется, так как сохраняется порядок векторов и ориентация тройки векторов. Следствие 2. Необходимым и достаточным условием компланарности трех векторов является равенство нулю их смешанного произведения. 12. Смешанное произведение векторов, заданных компонентами в декартовых координатах. Теорема 4.7. Если три вектора представлены разложениями по базису
то их смешанное произведение равно следующему определителю:
Доказательство. Из формулы (4.15) следует, что:
Умножив скалярно этот вектор на вектор
Полученное выражение (4.23) есть разложение определителя (4.22) по элементам третьей строки. Теорема доказана.
13. Уравнение первой степени и прямая на плоскости. Общее уравнение прямой. Нормальный вектор. Прямая в отрезках. Определение 5.1. Уравнение называется уравнением линии на плоскости относительно заданной системы координат, если ему удовлетворяют координаты точек, принадлежащих некоторой линии Определение 5.2. Линия называется алгебраической, если в некоторой прямоугольной системе координат Алгебраическая линия называется линией Теорема 5.1. Если линия в некоторой прямоугольной системе координат определяется алгебраическим уравнением степени Без доказательства. Теорема 5.2. Если на плоскости фиксирована прямоугольная система координат Доказательство. При специальном выборе системы координат, если ось Пусть уравнение прямой имеет вид:
Пусть задана точка
Вычитая (5.2) из (5.1), получаем:
Дадим векторное истолкование уравнения (5.3). Пусть Очевидно, что скалярное произведение
является условием ортогональности векторов Вектор Уравнение прямой в отрезках.
|
|||||||
|
Последнее изменение этой страницы: 2017-01-26; просмотров: 409; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.220.160.216 (0.028 с.) |
 (4.1)
(4.1)
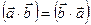 ,
, , где
, где  − число,
− число,
 , если
, если  ,
,  , если
, если  .
. = |a|2
= |a|2 и
и 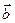 представлены в виде разложений по базису
представлены в виде разложений по базису  ,
, , то скалярное произведение этих векторов равно следующему выражению:
, то скалярное произведение этих векторов равно следующему выражению: 


 , обозначаемый символом
, обозначаемый символом и удовлетворяющий трем требованиям:
и удовлетворяющий трем требованиям:
 является правой.
является правой. , (антиперестановочность)
, (антиперестановочность)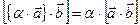 ,
, ,
, .
. равняется площади
равняется площади  параллелограмма, построенного на приведенных к общему началу векторах
параллелограмма, построенного на приведенных к общему началу векторах  , то их векторное произведение имеет вид:
, то их векторное произведение имеет вид: 
 , (4.13)
, (4.13) (4.14)
(4.14)
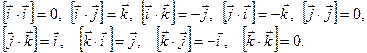 (4.16)
(4.16) .)
.)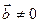 , то доказательство необходимости и достаточности утверждения теоремы следует из (4.12) и того факта, что условие
, то доказательство необходимости и достаточности утверждения теоремы следует из (4.12) и того факта, что условие  при
при  также является необходимым и достаточным.
также является необходимым и достаточным. называется смешанным произведением векторов
называется смешанным произведением векторов  и
и  равно объёму параллелепипеда, построенного на приведенных к общему началу векторах
равно объёму параллелепипеда, построенного на приведенных к общему началу векторах  левая. Если же перемножаемые вектора компланарны, то их смешанное произведение ровно нулю.
левая. Если же перемножаемые вектора компланарны, то их смешанное произведение ровно нулю.
 (4.20)
(4.20) и
и  .
. (4.21)
(4.21)
 ,
, (4.22)
(4.22)
 (4.23)
(4.23) (5.1)
(5.1) , и не удовлетворяют координаты точек, не принадлежащих этой линии.
, и не удовлетворяют координаты точек, не принадлежащих этой линии.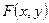 есть полином некоторой степени.
есть полином некоторой степени. - го порядка если
- го порядка если  , то любая прямая
, то любая прямая  совпадает с прямой, уравнение прямой «
совпадает с прямой, уравнение прямой « » совпадает с уравнением оси
» совпадает с уравнением оси  (общее уравнение прямой),
(общее уравнение прямой), (5.1)
(5.1) , координаты которой удовлетворяют уравнению.
, координаты которой удовлетворяют уравнению. . (5.2)
. (5.2) . (5.3)
. (5.3) и
и  − координаты некоторого вектора
− координаты некоторого вектора  , а
, а  и
и  −компоненты вектора
−компоненты вектора 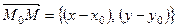 , начало которого совпадает с точкой
, начало которого совпадает с точкой  , а конец совпадает с произвольной точкой
, а конец совпадает с произвольной точкой  , принадлежащей прямой.
, принадлежащей прямой.
 и
и  .
. называется нормальным вектором прямой.
называется нормальным вектором прямой.



