
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Лабораторная работа № 3 измерение ускорения свободного паденияСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Цель работы Целью работы является измерение ускорения свободного падения тела при помощи математического маятника. При выполнении работы студенты знакомятся со свойствами маятника, изучают закономерности свободных колебаний тела, подвешенного на нити, под действием силы тяжести.
Оборудование Маятник, представляющий собой шарик, подвешенный на нити, секундомер, измерительная линейка.
Метод измерений По прямым измерениям периода колебаний математического маятника, выполненным при различных значениях длины нити подвеса маятника определяют ускорение свободного падения.
Подготовка к работе В ходе домашней подготовки к выполнению лабораторной работы студенты знакомятся с теоретической частью (п. 4.5) настоящего методического указания. Кроме того, ими подготавливается бланк отчета по лабораторной работе, содержащей титульный лист (см. Приложение А); цель работы (п. 4.1); краткое описание экспериментального оборудования (п. 4.2); письменные ответы на контрольные вопросы (п. 4.8) при использовании теоретической части (п. 4.5) и рекомендуемой литературы (п. 4.9).
Теоретическая часть Закономерности движения планет и их спутников, падения тел на Землю, движения артиллерийских снарядов, колебаний маятников свидетельствуют о существовании сил взаимного притяжения тел друг к другу. Эти силы подчиняются закону всемирного тяготения (гравитации), установленному И. Ньютоном в 1687 г.: между всякими двумя материальными точками действует сила всемирного тяготения, прямо пропорциональная произведению масс этих точек (m 1 и m 2) и обратно пропорциональная квадрату расстояния r между ними:
Коэффициент пропорциональности g называют гравитационной постоянной или постоянной тяготения. Как видно из уравнения (4.1), гравитационная постоянная численно равна силе взаимного тяготения двух материальных точек, массы которых одинаковы и равны единице массы, а расстояние между точками равно единице длины. Из опытов получено следующее значение гравитационной постоянной: g = 6,67×10-11 Сила F тяготения к Земле каждого находящегося на ней тела направлена к центру Земли и численно равна:
где m и M – массы тела и Земли, R – расстояние от тела до центра Земли. Наблюдения показывают, что сила F вызывает два вида движения тела. Во-первых, тело, лишенное опоры, падает на Землю. Во-вторых, тело участвует в суточном вращении Земли, т.е. движется по окружности, плоскость которой перпендикулярна к оси вращения Земли. Поэтому силу тяготения F целесообразно разложить на две составляющие: F = P + Fц. (4.3) Центростремительная сила Fц обусловливает участие тела в суточном вращении Земли. Сила Р вызывает падение незакрепленного тела на Землю. Ее называют силой тяжести тела. Движение тела под действием одной только силы тяжести Р называют свободным падением, а ускорение g, приобретаемое при этом телом, называют ускорением свободно падающего тела. По второму закону Ньютона
где R – радиус поверхности Земли, h – расстояние от центра тяжести тела до поверхности Земли. Вблизи поверхности Земли h << R, но с подъемом на 1 км. Ускорение силы тяжести уменьшается приблизительно на 0,03 %. Нешарообразность формы Земли и влияние суточного вращения приводят к тому, что ускорение силы тяжести g оказывается зависящим от географической широты места, изменяясь от 9,83 м / с 2 на полюсах до 9,78 м / с 2 на экваторе. На широте 45о оно равно 9,80665 м / с 2 и называется "нормальным ускорением". Определить численное значение ускорения свободного падения тела в данной точке местности можно с помощью математического маятника.
Маятник – твердое тело, совершающее под действием приложенных сил колебания около неподвижной точки или оси. В физике под маятником обычно понимают маятник, совершающий колебания под действием силы тяжести. Простейший маятник (рисунок 4.1) состоит из небольшого массивного груза С, подвешенного на нити длиной l. Если считать нить нерастяжимой и пренебречь размерами груза по сравнению с длиной нити, а массой нити по сравнению с массой груза, то груз на нити можно рассматривать как материальную точку, находящуюся на неизменном расстоянии l от точки подвеса О. Такой маятник называется математическим маятником. Если колеблющееся тело нельзя рассматривать как материальную точку, то маятник называют физическим. Свойства маятников широко используются в различных приборах: часах, приборах для определения силы тяжести (маятниковый прибор), ускорений движущихся тел, колебаний земной коры (сейсмограф), в гироскопических приборах, приборах для экспериментального определения моментов инерции тел и др.
Устройство и принцип работы Используемый в данной работе маятник (рисунок 4.1) состоит из небольшого массивного груза С, подвешенного на нити длиной l. Если маятник, отклоненный от равновесного положения Со, отпустить без начальной скорости или сообщить точке С скорость, перпендикулярную ОС и лежащую в плоскости начального отклонения, то маятник будет совершать колебания в одной вертикальной плоскости. Когда сообщенная маятнику начальная энергия очень мала (h << l), маятник совершает малые колебания, близкие к гармоническим, период малых колебаний можно приближенно считать равным:
где l – длина нити маятника, g – ускорение свободного падения, т.е. не зависящим от амплитуды. Формула (4.5) дает погрешность до 0,05 % при j =5о и до 1 % при j =23о. Эти результаты справедливы для инерциальной системы отсчета. По отношению к Земле вследствие ее суточного вращения плоскость качаний маятника медленно изменяет свое направление.
|
|||||
|
Последнее изменение этой страницы: 2017-01-24; просмотров: 1091; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.146.206.87 (0.011 с.) |

 . (4.1)
. (4.1) .
. , (4.2)
, (4.2)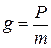 . Воспользовавшись уравнением
. Воспользовавшись уравнением  , найдем:
, найдем: , (4.4)
, (4.4) Рисунок 4.1 – Математический маятник
Рисунок 4.1 – Математический маятник
 , (4.5)
, (4.5)


