
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Погрешности измерений физических величин
Различают прямые и косвенные измерения. При прямых измерениях искомое значение величины находят непосредственно из опытных данных. Например: измерение длины линейкой или штангенциркулем, измерение температуры термометром и т.д. При косвенных измерениях искомое значение величины находят на основании известной зависимости между этой величиной и величинами, получаемыми прямыми измерениями. Например, определение плотности тела по измерениям его массы и геометрических размеров. Прямые измерения. В зависимости от причин, их вызывающих, ошибки измерения делят на случайные, систематические и грубые. Под случайными ошибками понимают ошибки, значения которых меняются от одного измерения к другому. Величина их не может быть установлена до опыта. Их возникновение вызвано неточностью измерения (случайными ошибками экспериментатора, неточным соблюдением методики измерения и т.д.) и непостоянством самой измеряемой величины (например, диаметра цилиндра или толщины пластины). Систематическая погрешность – это составляющая погрешности измерения, остающаяся постоянной или закономерно изменяющаяся при повторных измерениях одной и той же величины. Она может быть учтена или исключена изменением метода измерения, введением поправок к показаниям приборов, учетом систематического влияния внешних факторов и т.п. (например, поправка, связанная с изменением длины измерительной линейки и тела в результате теплового расширения). Грубые ошибки (промахи) являются также случайными, однако причиной грубых ошибок обычно являются неисправность измерительной техники или ошибки в работе экспериментатора. Поэтому, когда грубые ошибки значительны, они обнаруживаются без большого труда и этот результат должен быть исключен. Основным объектом изучения теории ошибок являются случайные ошибки при отсутствии систематических ошибок. Если какая-либо величина измеряется в одинаковых условиях несколько раз, то возникает необходимость в статистической обработке результатов измерений этой величины, чтобы учесть и оценить случайные ошибки. Обозначим х 0 не известное нам точное значение измеряемой величины. Произведя n измерений, получим х 1, х 2, х 3,..., хn – значения измеряемой величины, которые называются результатами наблюдения. Величины хi (i = 1, 2, 3,..., n) отличаются друг от друга и от х 0. Если величины хi измерены с одинаковой точностью, то для оценки х 0 применяют среднее арифметическое значение результатов наблюдений:
Среднее арифметическое
Следует отметить, что величина D хi значительно меньше величины хi. При большом числе измерений влияние каждого отдельного результата наблюдения хi на величину Абсолютная погрешность результата измерений D х, равная отклонению
Так как величина х 0 нам не известна, оценим величину D х через D хi. D х состоит из многих случайных величин D хi, из которых ни одна не доминирует над остальными. При этом условии случайные погрешности D хi подчиняются нормальному закону распределения Гаусса, который можно записать в виде
где функция Для серии n измерений среднеквадратичную погрешность наиболее точно можно оценить по формуле
Эта формула тем справедливее, чем больше число измерений. Однако в 1908 г. В. Госсет (псевдоним "Стьюдент") доказал, что статистический подход справедлив и при малом числе измерений. Остановимся на понятии доверительная вероятность w измерений. Выбранное значение доверительной вероятности (например, w = 0,9) означает, что при достаточно большом числе измерений примерно 90 % их приведет к результатам, отличающимся от истинного не более, чем на Доверительную границу погрешности D х для заданной w и при малом n определяют по формуле
где
Таблица 2.1 – Значения коэффициента Стьюдента
Обычно в лабораторных работах считается достаточной доверительная вероятность w = 0,9. Окончательный результат измерения представляется в виде:
что означает: измеряемая величина принадлежит интервалу значений Для сравнения точности измерений величин обычно вычисляется относительная погрешность
По величине относительной погрешности удобно сравнивать и результаты измерений однородных величин. Косвенные измерения. Обычно приходится вычислять искомую величину по результатам измерений других величин, связанных с этой величиной определенной функциональной зависимостью. Такие измерения называются косвенными. Например, плотность тела (пластины) определяется через массу тела и его объем, например, для пластины:
где L, b, h – линейные размеры пластины. Величины m, L, b, h можно измерить, а затем вычислить плотность. Итак, чаще всего искомая величина является функцией нескольких переменных:
Если величины x, y, z,... случайны, то А тоже будет случайной величиной. Из теории вероятностей известно, что среднее значение функции случайной величины приближенно равно функции от средних значений ее аргументов при условии, что погрешности измерений аргументов D х, D y, D z,... малы по сравнению с величинами x, y, z,.... То есть можно записать
где Для оценки доверительной границы случайной погрешности косвенного измерения можно использовать приближенный метод, который заключается в следующем. Если распределения величин хi, yi, zi,... нормальные (i – порядковый номер измерения), то распределение величины Аi тоже будет нормальным, поэтому для определения доверительной границы случайной погрешности косвенного измерения D Агр можно применить метод обработки случайных погрешностей прямых измерений. С этой целью найдем значения
для каждого номера измерений. Аналогично формуле (2.2) рассчитаем величины D Аi:
Доверительная погрешность D Агр при малом числе измерений (расчетов) определяется аналогично формулам (2.5), (2.6):
где tw,n – коэффициенты Стьюдента (см. таблицу 2.1) для заданных w и n. Результат косвенного измерения величины А представляется в форме
Относительная величина случайной погрешности косвенного измерения определяется, как и в случае прямых измерений, по формуле
Плотность тела Плотностью тела называется величина, измеряемая массой вещества, заключенной в единице объема тела. Средняя плотность выражается формулой
где m – масса тела, кг; V – объем тела, м 3. Единицей плотности является кг / м 3. Масса – физическая величина, одна из основных характеристик материи, определяющая ее инерционные и гравитационные свойства. В соответствии с принципом эквивалентности инертная и гравитационная массы численно равны. Весом тела называют силу, с которой тело вследствие его притяжения к Земле действует на связь (опору или подвес). Поэтому можно определять массу тела взвешиванием на рычажных весах. При этом сравнивают веса тела и разновесков. Когда весы уравновешены, можно утверждать, что вес тела равен весу разновесков. Но если равны веса тел, то равны и их массы. Так как на разновесках указаны именно массы, то массу тела мы определяем, просто сложив числа, указанные на разновесках.
|
|||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-01-24; просмотров: 313; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.227.24.209 (0.013 с.) |
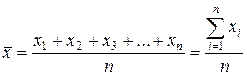 . (2.1)
. (2.1) называется результатом измерений. Поскольку величины результатов наблюдений хi носят случайный характер, то результат измерения – величина
называется результатом измерений. Поскольку величины результатов наблюдений хi носят случайный характер, то результат измерения – величина  . (2.2)
. (2.2) . (2.3)
. (2.3) , (2.4)
, (2.4) носит название функции Гаусса; s – средняя квадратичная погрешность результата наблюдения.
носит название функции Гаусса; s – средняя квадратичная погрешность результата наблюдения. . (2.5)
. (2.5) . Понятно, что большее значение доверительной вероятности соответствует большему значению погрешности наших измерений.
. Понятно, что большее значение доверительной вероятности соответствует большему значению погрешности наших измерений. , (2.6)
, (2.6) – коэффициент Стьюдента, зависящий от доверительной вероятности w и числа измерений n, находится по таблице 2.1 для заданных w и n.
– коэффициент Стьюдента, зависящий от доверительной вероятности w и числа измерений n, находится по таблице 2.1 для заданных w и n. , (2.7)
, (2.7) c доверительной вероятностью w.
c доверительной вероятностью w. . (2.8)
. (2.8) , (2.9)
, (2.9) . (2.10)
. (2.10) , (2.11)
, (2.11) – среднее значение величины А;
– среднее значение величины А;  – средние значения величин x, y, z,... (см формулу 2.1).
– средние значения величин x, y, z,... (см формулу 2.1). и
и  (2.12)
(2.12) . (2.13)
. (2.13)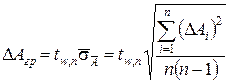 , (2.14)
, (2.14) . (2.15)
. (2.15) . (2.16)
. (2.16) , (2.17)
, (2.17)


