
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Лабораторная работа № 8 изучение дифракции света от отверстия и преградыСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Цель работы Исследуя картину дифракции от отверстия и преграды, определить длину световой волны и размеры преграды.
Оборудование Гелий-неоновый лазер ЛГ-209, прямоугольная щель, нить, пластина с круглым отверстием, пластина с мелкими круглыми частицами, метровая линейка, экран с полоской миллиметровой бумаги.
Метод измерений По прямым измерениям расстояния между минимумами k -ого порядка и диаметра светлого пятна определяют длину световой волны и размеры преграды.
Подготовка к работе В ходе домашней подготовки к выполнению лабораторной работы студенты знакомятся с теоретической частью (п. 9.5) настоящего методического указания. Кроме того, ими подготавливается бланк отчета по лабораторной работе, содержащей титульный лист (см. Приложение А); цель работы (п. 9.1); краткое описание экспериментального оборудования (п. 9.2); письменные ответы на контрольные вопросы (п. 9.8) при использовании теоретической части (п. 9.5) и рекомендуемой литературы (п. 9.9).
Теоретическая часть Дифракция света представляет собой отклонение света от прямолинейного распространения. Это явление возникает при наличии какого-либо препятствия на пути света (узкая щель, малое отверстие и т. д.). Дифракция в параллельных лучах впервые была рассмотрена И. Фраунгофером (1821 – 1822 гг.). Пусть плоская монохроматическая волна длиной l падает на непрозрачную преграду с узкой целью АВ, имеющей постоянную ширину b =| АВ | и длину l >> b (рисунок 9.1 а). По принципу Гюйгенса каждая точка, до которой дошла волна, является источником вторичных сферических волн. Поэтому из каждой точки отверстия по всем направлениям будут распространяться волны. Рассмотрим волны, падающие в точку K экрана. Если расстояние от щели до экрана L значительно больше ширины щели, то можно считать, что все они дифрагируют под одним и тем же углом j. В точке K накладывающиеся волны интерферируют. Результат интерференции зависит от разности хода волн D=| AC |, попадающих в точку K от краев щели.
а) б) в) Рисунок 9.1 – Дифракция света от отверстия
Для нахождения разности хода волн D из точки В опустим перпендикуляр ВС на прямую AK. Из треугольника АВС (рисунок 9.1) следует: D= b sinj, (9.1) где b – ширина щели; j - угол дифракции.
Мысленно разобьем линию АС на ряд отрезков длиной
В промежутках между минимумами будут наблюдаться максимумы освещенности:
В этом случае фронт АВ разбивается на нечетное число зон Френеля z = 2 k + 1 и одна из зон остается непогашенной. Пусть угол дифракции j = 0, тогда все волны приходят в точку О экрана без разности хода (в одной фазе). Они усиливают друг друга, образуя центральный максимум нулевого порядка. Таким образом, дифракционная картина при освещении щели параллельным пучком лучей монохроматического света имеет вид чередующихся светлых и темных полос с широкой светлой полосой в центре – центральным максимум (рисунок 9.1 б). Интенсивность максимумов по мере удаления от центрального максимума убывает. В случае дифракции Фраунгофера на круглом отверстии диаметра D дифракционное изображение состоит из центрального светлого пятна (диск Эйри), на которое приходится приблизительно 85 % энергии света, и окружающих его светлых и темных колец (рисунок 9.1 в). Кольцевые максимумы убывают по интенсивности еще быстрее, чем в случае отверстия прямоугольной формы. Положение максимумов и минимумов удовлетворяет условию:
где D – диаметр отверстия; j ‑ угол дифракции; l ‑ длина волны света; k – целые числа; значения mmax и mmin для k = 1, 2, 3 и 4 приведены в таблице 9.1. Таблица 9.1
Следовательно, первому минимуму соответствует выражение:
Измерения толщины тонкой нити или диаметра мелких частиц размерами в несколько микрон являются сложной задачей. Эта проблема может быть решена дифракционным методом с весьма высокой точностью. Рассмотрим дифракцию от нити и мелкой круглой частицы. Воспользуемся для этой цели теоремой Бабине. Согласно этой теореме дифракционные картины от преграды (нить, мелкая круглая частица и т. п.) и от равного ей по размеру отверстия (щель, круглое отверстие и т. п.) должны быть совершенно одинаковы вне области свободного (прямого) пучка. Убедимся, что это действительно так. Рассмотрим некоторую точку экрана. Пусть в этой точке амплитуда волны, дифрагирующей от преграды (нить, мелкая круглая частица и т. п.) в данном направлении, равна Таким образом, дифракционные картины от нити толщиной b или мелкой круглой частицы диаметра D (вне области прямого пучка) будут такими же, как и от щели, ширина которой равна толщине нити или круглого отверстия диаметр которого равен диаметру мелкой круглой частицы (в случае круглой частицы центральное светлое пятно называется пятном Пуассона). Раз так, то для расчета дифракции от нити/мелкой круглой частицы можно воспользоваться теми же формулами (9.2 – 9.5), что и для щели/круглого отверстия.
Устройство и принцип работы Схема установки дана на рисунке 9.3. Параллельный монохроматический пучок света от лазера 1 падает на ширму 2 с отверстием или преградой. Дифракционная картина отображается на сплошной экран 9. С помощью линейки 4 измеряется расстояние между ширмой с прямоугольной щелью/отверстием и экраном. Лазер располагают на расстоянии 0,5 – 2 м от экрана.
|
||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-01-24; просмотров: 682; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.191.189.119 (0.01 с.) |


 Рисунок 9.2 – Схема разбиения линии АС на z отрезков
Рисунок 9.2 – Схема разбиения линии АС на z отрезков
 (рисунок 9.2). На АС = b sinj уложится
(рисунок 9.2). На АС = b sinj уложится 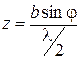 таких отрезков. Проведя из концов этих отрезков линии, параллельные ВС, до встречи их с АВ, мы разобьем фронт волны в щели на ряд полосок одинаковой ширины. Эти полоски и являются в данном случае зонами Френеля. Волны, идущие от каждых двух соседних зон Френеля, приходят в точку К в противоположной фазе и гасят друг друга. Если при таком построении число зон окажется четным, z = 2 k (где k – целое число, не равное нулю, k = 1, 2, 3, …), то каждая пара соседних зон взаимно погасит друг друга и при данном угле j на экране будет минимум освещенности. Условие образования минимума имеет вид:
таких отрезков. Проведя из концов этих отрезков линии, параллельные ВС, до встречи их с АВ, мы разобьем фронт волны в щели на ряд полосок одинаковой ширины. Эти полоски и являются в данном случае зонами Френеля. Волны, идущие от каждых двух соседних зон Френеля, приходят в точку К в противоположной фазе и гасят друг друга. Если при таком построении число зон окажется четным, z = 2 k (где k – целое число, не равное нулю, k = 1, 2, 3, …), то каждая пара соседних зон взаимно погасит друг друга и при данном угле j на экране будет минимум освещенности. Условие образования минимума имеет вид: . (9.2)
. (9.2)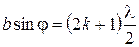 . (9.3)
. (9.3) , (9.4)
, (9.4) . (9.5)
. (9.5) , а для соответствующего дополнительного экрана (щель, круглое отверстие и т. п.) в том же направлении амплитуда дифракционной волны равна
, а для соответствующего дополнительного экрана (щель, круглое отверстие и т. п.) в том же направлении амплитуда дифракционной волны равна  . В отсутствии обоих экранов (преграды и отверстия) амплитуды волн для всех направлений, кроме направления первоначального пучка, равны 0. Следовательно,
. В отсутствии обоих экранов (преграды и отверстия) амплитуды волн для всех направлений, кроме направления первоначального пучка, равны 0. Следовательно,  . Отсюда
. Отсюда  , а значит равны интенсивности света.
, а значит равны интенсивности света.


