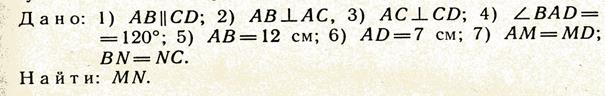Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Чертеж и краткая запись условия геометрической задачи.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Основная особенность геометрических задач состоит в том, что их решение практически всегда сопровождается на том или ином этапе (иногда на нескольких) построением схематического чертежа–наброска, или, в некоторых случаях, полноценного чертежа. Правильное выполнение простейшего чертежа, как и его чтение, – одни из важнейших компетенций, необходимых каждому человеку в его повседневной, а во многих случаях и профессиональной деятельности. С методической точки зрения чертеж – важнейшее средство наглядности, значение которого для обучения геометрии трудно переоценить. Особенно значительную роль играют чертежи в курсе геометрии основной школы, так как они, в отличие от старших классов, достаточно легко выполнимы и отражают истинное положение фигуры на плоскости. При построении чертежа следует выполнять ряд требований. Сформулируем основные из них [23. С. 17–18]. 1. Чертеж должен представлять собой схематический рисунок основного объекта задачи (геометрической фигуры, или совокупности фигур, или какой–то части этих фигур). 2. Все элементы фигуры и некоторые ее характеристики должны быть обозначены на чертеже с помощью букв и других знаков. Если в тексте задачи указаны какие–либо обозначения фигуры или ее элементов, то эти обозначения должны быть и на чертеже; если же в тексте никаких обозначений нет, то следует воспользоваться общепринятыми или наиболее удобными в данном конкретном случае. 3. Чертеж к геометрической задаче должен отражать наиболее общий случай вида и расположения основного ее объекта. Это означает, что если в задаче в качестве основного объекта назван, например, треугольник и при этом не указан его вид, то следует построить разносторонний непрямоугольный треугольник. Или если в задаче основным объектом является трапеция, то не следует строить равнобедренную или прямоугольную трапецию и т.д. 4. При выполнении чертежа желательно соблюдать заданные в условии пропорции в построении отдельных элементов фигуры. Это не значит, что необходимо строго выдерживать масштаб. Однако, если по условию задачи сторона АВ треугольника АВС наибольшая, то это должно быть соблюдено на чертеже. Или если задана медиана треугольника, то она должна проходить через одну из вершин и приблизительно через середину противоположной стороны. Надо соблюдать также такие заданные в условии задачи отношения, как параллельность, перпендикулярность и т.п. 5. Чертеж существенно облегчит процесс решения задачи, если он верен, легко выполним, нагляден. Построение чертежа, как правило, сопровождает краткая запись всех условий и требований геометрической задачи. В ней, пользуясь принятыми на чертеже обозначениями, записываются все характеристики и отношения, указанные в условии задачи. При этом названия фигур или отдельных ее частей следует заменять схематической записью их определений. Так, вместо того, чтобы писать, что ABCD – трапеция, лучше записать, что AB ║ CD. В краткой записи, так, где это возможно и целесообразно, следует использовать стандартный математический символический язык, т.е. знаки =, ║, Заметим, что эти рекомендации не носят тотального характера, при решении некоторых геометрических задач чертеж и краткая запись могут быть выполнены иначе. Приведем пример построения чертежа и выполнения краткой записи одной интересной геометрической задачи[4]. Пример. Задача. Диагональ трапеции перпендикулярна к ее основаниям; тупой угол, прилежащий к ее основанию, равен 120˚, а боковая сторона, прилежащая к нему, равна 7 см; большее основание равно 12 см. Найти среднюю линию трапеции. Основной объект задачи – трапеция, в которой одна из диагоналей перпендикулярна ее основаниям. Если начинать чертить эту трапецию обычным способом с построения ее сторон, ошибка практически неизбежна, т.к. нестандартное положение занимает диагональ трапеции: она должна быть перпендикулярна ее основаниям. Поэтому наиболее оптимальный путь – построение этой диагонали, которую можно представить в качестве вертикального отрезка, от концов которого строятся два горизонтальных отрезка, – основания трапеции, направленные в разные стороны от диагонали. Строим тупой (по условию) угол при большем (обычно нижнем) основании. Вторая его сторона пересечет меньшее основание в одной из вершин трапеции. Достраиваем трапецию, придерживаясь заданных пропорций, проводим в ней среднюю линию, вводим стандартные обозначения тупого угла при большем основании (Рис. 5).
|
||||
|
Последнее изменение этой страницы: 2017-01-24; просмотров: 2389; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.117.106.23 (0.009 с.) |

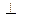 и т.п.
и т.п. Рис. 5.
Рис. 5.