
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Роль и функции геометрических задач.Содержание книги
Поиск на нашем сайте
Роль и функции задач в обучении геометрии в основной школе во многом определяются целью изучения курса геометрии в VII–IX классах, которая сформулирована а программах по математике следующим образом: «Целью изучения курса геометрии в VII–IX классах является систематическое изучение свойств геометрических фигур на плоскости, формирование пространственных представлений, развитие логического мышления и подготовка аппарата, необходимого для изучения смежных дисциплин (физика, черчение и т.д.) и курса стереометрии в старших классах» [18. С. 8.]. Итак, в качестве обучающей цели курса геометрии VII-IX классов в программах по математике является систематическое изучение свойств геометрических фигур на плоскости; в качестве развивающей цели – формирование пространственных представлений и развитие логического мышления; пропедевтическая цель состоит в подготовке аппарата, необходимого для изучения смежных дисциплин и стереометрии. Геометрические задачи эффективно способствуют достижению всех сформулированных в программе целей курса геометрии VII-IX классов. Систематическое решение задач способствует сознательному и прочному усвоению теории геометрии, помогает увидеть ее практическую ценность, формирует ключевые компетенции в области геометрии. Геометрические задачи, как и другие математические задачи, выполняют воспитательные, развивающие и обучающие функции. Осуществляя подбор задач для урока, учитель может преследовать различные цели, используя различные функции той или иной задачи на различных этапах урока. · Задача может предварять какое–либо теоретическое положение Пример. [2] Перед доказательством признака равенства треугольников по трем сторонам можно предложить следующие задачи: а) Д а н о: АВ = ВС; АD = СD.(Рис. 1). Д о к а з а т ь:
б) Д а н о: в четырехугольнике АBCD: АВ = АD; ВС = СD (Рис. 2.). Д о к а з а т ь:
· Решение задачи может служить источником получения новых знаний по геометрии. Тогда полезно к условию задачи сформулировать некоторую последовательность заданий–требований. Пример. Задача. Через точку М внутри круга проведены две хорды АB и CD. Доказать, что треугольники AMC и DMB подобны (Рис. 3).
Последовательность заданий–требований может быть такая: – Записать пропорциональность сходственных сторон. – Сравнить произведение отрезков хорды CD, на которые их делит точка М. – Провести диаметр через точку М и сравнить произведение отрезков диаметра с произведениями отрезков каждой из хорд, проходящих через точку М. – Сформулировать полученное предложение. · Задача по геометрии может выполнять роль демонстрации практической значимости геометрии. Далее мы будем говорить специально о такого рода задачах, рассматривая классификации геометрических задач. Пример. Задача. Длина тени, отбрасываемой деревом, равна 8,7 м, в то время как длина тени палки, воткнутой вертикально в землю, равна 1,2 м. Определить высоту дерева, если длина палки равна 0,88 м.
|
||||
|
Последнее изменение этой страницы: 2017-01-24; просмотров: 417; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.8.79 (0.005 с.) |

 и помогает отыскать его или усмотреть некоторую геометрическую зависимость. Тогда в задачи включают отдельные элементы доказательства теоремы. Рассмотрим пример.
и помогает отыскать его или усмотреть некоторую геометрическую зависимость. Тогда в задачи включают отдельные элементы доказательства теоремы. Рассмотрим пример. BAD =
BAD = 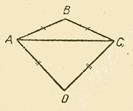 Рис. 1.
Рис. 1. Рис. 2.
Рис. 2.  Рис. 3.
Рис. 3. Рис. 4.
Рис. 4. 


