
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Влияние трения на реакции в кинематических парахСодержание книги
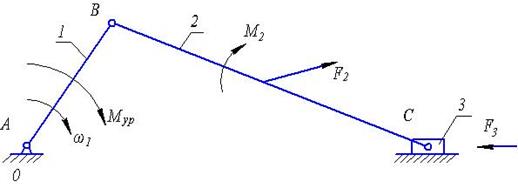
Поиск на нашем сайте В поступательной паре (рис.4.19) полная реакция между звеньями отклоняется за счет силы трения F тр 12 от нормали n-n на угол j, называемый углом трения, в сторону, противоположную относительной скорости V12.
В кинетостатическом расчете с учетом трения удобно определять раздельно нормальную Fn12 составляющую полной реакции, обозначая ее (как и в силовом расчете без учета трения) F12, и силу трения Fтр12, учитывая их связь между собой:
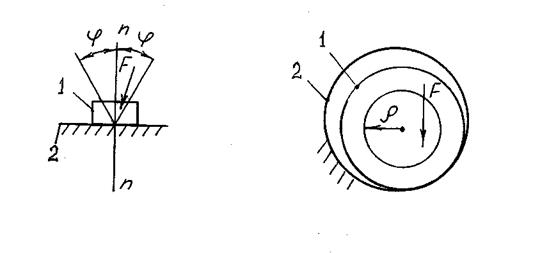
Fтр12 = f· F12 = F12·tgj, (4.13) Здесь j = arctg f (4.14) - угол трения в поступательной паре, f - коэффициент трения скольжения, зависящий от состояния (обработки) трущихся поверхностей, материалов взаимодействующих тел, наличия и свойств смазки, условий работы и т.д. Число неизвестных при выполнении силового расчета остается прежним - это величина и точка приложения реакции, определяемая плечом hx. Во вращательной паре (рис.4.20,а) вал 1, вращаясь в направлении w12, при наличии трения между валом и опорой, будет «набегать» на опору. При этом полная реакция F12 будет отклоняться от нормали на угол трения j¢, располагаясь по касательной к окружности, называемой кругом трения. При этом радиус круга трения
Так как углы трения малы, то можно считать, что sinj¢»tgj¢. Тогда радиус круга трения будет приближенно равен r=r·tgj¢=r· f ¢, (4.16) где f ¢ - коэффициент трения во вращательной паре. При силовом расчете с учетом трения удобно полную реакцию F12 переносить в центр вала и учитывать момент (рис.4.20,б), появляющийся при таком переносе. Этот момент называют моментом трения М тр: Мтр=F12×r=F12·r· f ¢. (4.17) Коэффициент трения f ¢ определяется экспериментально для различных условий работы вращательных пар и изменяется в зависимости от материалов, состояния трущихся поверхностей, от условий работы и т.п. Как и в силовом расчете без учета трения при определении реакции между звеньями неизвестны две величины - модуль реакции и направление ее действия. В обоих рассмотренных низших кинематических парах число неизвестных при определении реакций между звеньями с учетом трения остается таким же, как и без учета трения. Т.е. группы Ассура статически определимы и при учете трения, и силовой расчет механизма надо выполнять, разбивая его на группы Ассура. Пример кинетостатического расчета кривошипно-ползунного механизма с учетом трения в кинематических парах Уравнения, необходимые для определения реакций, действующих на звенья двухповодковой группы Ассура 2-3 (рис.4.21,б), с учетом трения в кинематических парах, будут иметь следующий вид: 1. Для звена 2: åМс = Ft21 BC ml - F2 h2 ml - M2 - M т р 21 - М тр23 = 0(4.18) 2. Для звеньев 2 и 3: å 3. Для звена 2: å
4. Для звена 3: åМс = F30 hx ml + Mтр32 = 0 (4.21)
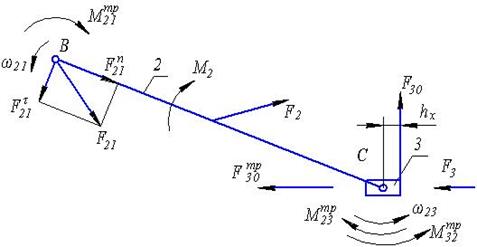
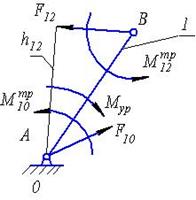
Моменты трения Мтр21 и Мтр23 и сила трения Fтр30, противоположны соответствующим относительным скоростям звеньев w21, w23, и V30, определяемым с помощью плана скоростей. По предложению академика Артоболевского И.И. кинетостатический расчет с учетом трения в кинематических парах выполняется методом последовательных приближений, который заключается в следующем. В первом приближении задача решается без учета трения, т.е. Мтр21 = Мтр23 = 0, Fтр30 = 0. Затем по найденным реакциям определяются моменты трения в шарнирах и силы трения в поступательных парах: Мтр21 = F21 f B rB Мтр23 = F23 f С rС Fтр30 = f 30 F30, (4.22) с учетом которых находятся уточненные значения реакций, т.е. выполняется второе приближение. По новым значениям сил вновь определяются моменты и силы трения и т.д. Задача считается решенной после того, как найденные в очередном приближении реакции отличаются от предыдущих значений на требуемую величину. Обычно ограничиваются вторым приближением. Уравнения, необходимые для кинетостатического расчета начального звена рассматриваемого механизма с учетом трения (рис. 4.21,в) будут следующими: å åМА = Мур - F12 h12 ml - Мтр12 -Мтр10 = 0, (4.24) где Мтр12 = F21fBrB и Мтр10 = F10 fA rA. (4.25) Самоторможение Это явление, при котором как бы велика ни была движущая сила, движение невозможно. а) Поступательная пара (рис.4.22,а). Если движущая сила находится внутри конуса трения, то движение невозможно, т.к. потенциально возможная сила трения всегда будет превосходить касательную составляющую от движущей силы. б) Вращательная пара (рис.4.22,б). Если сила, стремящаяся вызвать вращение вала, пересекает круг трения, то движения не будет. Если сила располагается по касательной к кругу трения, то вал будет вращаться равномерно.
|
|||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-01-26; просмотров: 684; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.009 с.) |


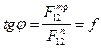 , (4.12)
, (4.12)

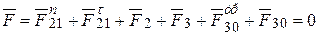 (4.19)
(4.19)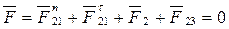 (4.20)
(4.20) (4.23)
(4.23)


