
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Уравнения движения и равновесия
Основным динамическим уравнением движения материальной точки является 2-й закон Ньютона · производная по времени от количества движения
равна сумме всех действующих на систему внешних сил
и называется уравнением количества движения, или уравнением импульсов:
· производная по времени от кинетического момента
системы относительно какого-либо неподвижного центра О равна сумме моментов
всех внешних сил, действующих на систему, относительно того же центра, т.е.
называется уравнением моментов количества движения; · Дифференциал кинетической энергии:
системы равен сумме элементарных работ
всех действующих на систему внешних
называется уравнением механической энергии (теоремой живых cил). · Для любого мысленно выделяемого индивидуального объёма сплошной среды
(соответственно количество движения, момент количества движения и кинетическая энергия сплошной среды в объёме
(соответственно сумма внешних объёмных и поверхностных сил и их моментов относительно некоторого неподвижного центра О, действующих на среду в объёме Сумма элементарных работ внешних и внутренних объёмных и поверхностных сил
В этом случае уравнения (6.7.1) и (6.7.2) являются основными постулируемыми динамическими соотношениями механики сплошной среды. Они служат исходными уравнениями для описания любых движений сплошной среды, в том числе разрывных движений и ударных процессов. Уравнение (6.7.3) одно из наиболее важных следствий уравнений (6.7.1) и (6.7.2) при непрерывных движениях в пространстве и времени. При непрерывных движениях интегральная теорема движения (6.7.1) эквивалентна следующим 3 дифференциальным уравнениям: · в декартовой системе координат:
· в цилиндрической системе координат при осевой симметрии
где проекции ускорения вычисляют по формулам (1.6). Эти уравнения, связывающие компоненты
При непрерывном движении сплошной среды, теорема моментов количества движения (6.7.2) в дифференциальной форме сводится к выводу о том, что тензор напряжений симметричен, т.е. Интегральная теорема живых сил (6.7.3) эквивалентна следующему дифференциальному уравнению:
где
соответственно изменение кинетической и потенциальной энергии бесконечно малого объёма сплошной среды, элементарная работа внешних объёмных и поверхностных сил, действующих на бесконечно малый элемент объёма среды. Уравнение (6.7.5) является следствием уравнения движения(6.7.4) и представляет собой уравнение баланса механической энергии. В общем случае оно не является законом сохранения энергии, но его можно так трактовать тогда, когда механическая энергия тела не переходит в тепловую или другие виды энергии. Общий закон сохранения энергии в этом случае распадается на два: · закон изменения механической энергии; · закон изменения энергии другого вида.
|
|||||
|
Последнее изменение этой страницы: 2017-01-26; просмотров: 192; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.218.184.214 (0.006 с.) |
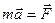 , а широко используемым следствием этого закона являются следующие общие теоремы движения системы материальных точек:
, а широко используемым следствием этого закона являются следующие общие теоремы движения системы материальных точек:
 (6.7.1)
(6.7.1)


 , (6.7.2)
, (6.7.2)

 и внутренних
и внутренних  сил, т.е.
сил, т.е. (6.7.3)
(6.7.3) , ограниченного поверхностью
, ограниченного поверхностью  , уравнения (1.68) - (1.70) действительны, если динамические величины определить следующим образом:
, уравнения (1.68) - (1.70) действительны, если динамические величины определить следующим образом: .
. ,
, .
.
 (6.7.4)
(6.7.4) вектора скорости и тензора напряжений
вектора скорости и тензора напряжений  , являются основной системой дифференциальных уравнений движения для любой сплошной среды, представляющих собой уравнение баланса количества движения (импульса) для бесконечно малого объёма среды. Если движения частиц происходят без ускорения (
, являются основной системой дифференциальных уравнений движения для любой сплошной среды, представляющих собой уравнение баланса количества движения (импульса) для бесконечно малого объёма среды. Если движения частиц происходят без ускорения ( ) или они пренебрежимо малы, то уравнения (6.7.4) называются дифференциальными уравнениями равновесия (т.е. установившийся поток).
) или они пренебрежимо малы, то уравнения (6.7.4) называются дифференциальными уравнениями равновесия (т.е. установившийся поток). . Если тензор напряжений симметричен, то уравнения моментов количества движения удовлетворяются тождественно.
. Если тензор напряжений симметричен, то уравнения моментов количества движения удовлетворяются тождественно. , (6.7.5)
, (6.7.5)



