Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Закон изменения кинетической энергии
Изменение кинетической энергии жидкого объёма за единицу времени равно мощности всех внешних и внутренних (поверхностных и массовых) сил, действующих на этот объём жидкости. Кинетическая энергия бесконечно малого объёма
Мощность силы равна скалярному произведению вектора силы и скорости тела, на которое она действует. Например, на элементарный объём
Мощность силы найдём как отношение совершаемой ею работы ко времени
Рассуждая аналогично, найдём мощность внешних поверхностных сил, действующих на поверхность
где Рассчитать работу внешних сил, как правило, не представляется возможным, так как она зависит от поля скорости внутри контрольного объёма, которое вообще говоря неизвестно. Поэтому введём функцию
Знак минус вводится, чтобы функция e(х,у,z,t) была всегда положительной. Приравнивая субстанциональную производную от кинетической энергии (6.5.1) сумме мощностей (6.5.2),(6.5.3) и (6.5.4), получаем уравнение, выражающее закон изменения кинетической энергии:
Если уравнение (6.5.5) используют для решения одномерных задач, то его представляют в виде различных модификаций уравнения Бернулли. Закон изменения кинетической энергии в виде дифференциального уравнения не используется, так как оно эквивалентно дифференциальному уравнению, выражающему закон изменения количества движения.
ЗАКОН СОХРАНЕНИЯ ЭНЕРГИИ В дополнение к закону изменения кинетической энергии, выражающему баланс механической энергии, рассмотрим более общий случай, принимая во внимание изменение механической энергии за счёт её источников (стоков), содержащихся внутри контрольного объёма, и баланс внутренней энергии (тепла).
Рис.6.3. Контрольный объём для формулировки закона сохранения энергии Пусть в контрольном объёме
Рассмотрим баланс тепла в контрольном объёме. Пусть
Чем могут быть вызваны изменения внутренней энергии жидкости внутри контрольного объёма? Возможны следующие причины: наличие внутри объёма источников тепла, подводимого извне, с плотностью распределения t(r,t) (на единицу объёма в единицу времени); присутствие на граничных поверхностях источников тепла с плотностью распределения s(r,t) (на единицу площади в единицу времени); работа внутренних сил в жидкости, например, за счёт вязкости; плотность распределения мощности внутренних сил e(r,t). Баланс тепла для жидкости, содержащейся в контрольном объёме в момент времени t, имеет вид
Складывая (6.6.1) и (6.6.3), получаем уравнение, выражающее общий закон сохранения энергии для контрольного объёма сплошной среды (6.6.4):
Как следует из полученного соотношения, работа внутренних сил Для перехода к Эйлерову неподвижному объему
здесь А – скалярная или векторная функция.
|
||||||
|
Последнее изменение этой страницы: 2017-01-26; просмотров: 154; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.188.175.182 (0.007 с.) |
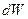 жидкости равна
жидкости равна 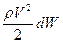 , тогда кинетическая энергия конечного объёма
, тогда кинетическая энергия конечного объёма  будет равна:
будет равна: . (6.5.1)
. (6.5.1)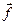 , величина этой силы равна
, величина этой силы равна 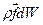 . Работа этой силы на перемещении
. Работа этой силы на перемещении  равна
равна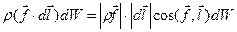 .
.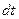 , за которое произойдёт перемещение объёма
, за которое произойдёт перемещение объёма 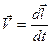 . Следовательно, мощность внешней объёмной силы для элементарного объёма
. Следовательно, мощность внешней объёмной силы для элементарного объёма 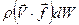 . Мощность этой силы при перемещении всего объёма
. Мощность этой силы при перемещении всего объёма  . (6.5.2)
. (6.5.2)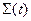 , ограничивающую объём
, ограничивающую объём 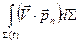 , (6.5.3)
, (6.5.3)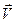 - скорость жидкости на поверхности
- скорость жидкости на поверхности  .
.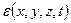 - плотность распределения мощности внутренних сил, т.е. работы, которая за единицу времени переходит в тепло и рассеивается (диссипирует) внутри объёма жидкости, имеющего единичную массу. Работа внутренних сил может только уменьшать кинетическую энергию, так как, переходя в энергию беспорядочного теплового движения молекул, соответствующая часть кинетической энергии объёма
- плотность распределения мощности внутренних сил, т.е. работы, которая за единицу времени переходит в тепло и рассеивается (диссипирует) внутри объёма жидкости, имеющего единичную массу. Работа внутренних сил может только уменьшать кинетическую энергию, так как, переходя в энергию беспорядочного теплового движения молекул, соответствующая часть кинетической энергии объёма 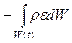 . (6.5.4)
. (6.5.4)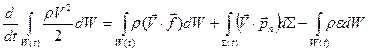 . (6.5.5)
. (6.5.5)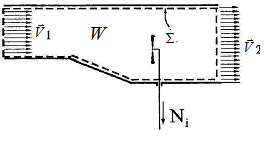
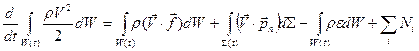 . (6.6.1)
. (6.6.1)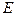 - количество внутренней энергии жидкости (теплоты) внутри контрольного объёма, а
- количество внутренней энергии жидкости (теплоты) внутри контрольного объёма, а 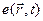 - плотность её распределения в пространстве, т.е. удельная внутренняя энергия жидкости (на единицу массы). Тогда
- плотность её распределения в пространстве, т.е. удельная внутренняя энергия жидкости (на единицу массы). Тогда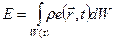 . (6.6.2)
. (6.6.2)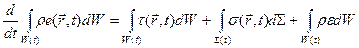 . (6.6.3)
. (6.6.3)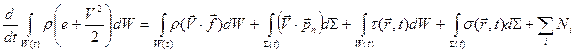 .
.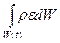 не изменяет полную энергию системы жидких частиц: она уменьшает механическую энергию и увеличивает тепловую.
не изменяет полную энергию системы жидких частиц: она уменьшает механическую энергию и увеличивает тепловую.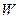 используется теорема о дифференцировании по времени функции, как интеграла по подвижному объему:
используется теорема о дифференцировании по времени функции, как интеграла по подвижному объему: