
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Физические свойства жидкостей и газовСодержание книги
Поиск на нашем сайте
Текучесть. Жидкие и газообразные тела отличаются от твёрдых тел свойством текучести. Если на твёрдое тело действуют малые неразрушающие силы, то они незначительно меняют его форму, т.е. относительное положение его частей. Если под действием сколь угодно малых внешних сил тело деформируется неограниченно, пока внутренние касательные напряжения в нём не станут равными нулю, то в этом случае реализуется свойство называемое текучестью. Многие физические тела двойственны по природе. Например, стекло, которое мы привыкли рассматривать как хрупкое твёрдое тело, под действием длительной нагрузки может вести себя как жидкость. Так оконные стёкла, простоявшие более 100 лет в нижней части толще, чем в верхней, так как под действием сил тяжести материал «стекает» вниз. С другой стороны, такая типичная жидкость как вода при быстром нагружении (ударе) ведёт себя как твёрдое тело. Попытаемся определить природу этой двойственности на молекулярном уровне. Благодаря действию сил притяжения и отталкивания расположение молекул в пространстве носит упорядоченный характер. Среднее характерное расстояние между молекулами жидкости и твёрдого тела примерно одинаковы и равны» (3¸4)10-8см. Под действием тепла молекулы движутся (хаотически колеблются) около положения равновесия, увеличивая с температурой амплитуду колебаний. В твёрдых телах амплитуда много меньше расстояния между молекулами, в жидкости - это величины одного порядка. Поэтому колебания молекул, совершаемые с амплитудой того же порядка, что и расстояния, могут приводить к тому, что молекулы могут перескакивать из одного места ячейки в другое. В некоторых жидкостях это случается чаще, в других - реже. Текучесть тела определяется характерным временем tr нахождения молекулы в каждой ячейке с момента попадания в неё до момента перескакивания в другую ячейку. Если время нахождения молекулы в ячейке много меньше времени действия силы, то за период действия силы молекулы могут многократно изменить своё положение в пространстве, т.е. позволяя силе непрерывно и необратимо деформировать тело (т.е. вести себя как текучая среда). Такое тело мы называем жидкостью. В противном случае мы имеем дело с твёрдым телом. С повышением температуры текучесть тела увеличивается. Для газообразных тел характерной особенностью является хаотическое движение и столкновение молекул в пространстве. Поэтому газы обладают не только текучестью, но и сжимаемостью.
Сжимаемость жидкостей и газов. Приложим силу DF и увеличим давление в объёме
Коэффициент объёмного сжатия имеет размерность (Па)-1. Знак минус вводится для того, чтобы отразить уменьшение объёма под действием сжатия, но для практических расчётов удобно иметь его положительным. Модулем объёмной упругости
Обе эти величины зависят от температуры и вида жидкости.Модуль объёмной упругости для воды при Т = 293°К равен Пример. Если на воду помимо атмосферного давления (ра =101325 Па или 1.033 кгс/см2), будет дополнительно действовать такое же давление, то объём воды уменьшится приблизительно на 1/20000, т.е. практически это заметить невозможно. Следовательно, воду и другие жидкости можно считать несжимаемыми и принимать их плотность постоянной (r = const), не зависящей от давления. Для газа можно достаточно эффективно использовать модель идеального газа, характеризуемую уравнением Клапейрона - Менделеева
где R - удельная газовая постоянная, не зависящая от плотности и температуры, но различная в зависимости от природы газа (например, для воздуха R = 287Дж/кгК). С помощью уравнения (1.5.3) можно найти плотность воздуха при атмосферном давлении и температуре окружающей среды равной 20ºС:
Из этого закона следует закон Бойля - Мариотта, устанавливающий изотермическую связь между давлением и плотностью:
для заданного объёма газа при постоянной температуре. Для адиабатического процесса (когда отсутствует теплообмен между выделенным объёмом газа и окружающей средой) характерна следующая зависимость:
где Отличие механики жидкости от механики газа. Несмотря на то, что свойство текучести является основным при изучении жидкостей и газа, тем не менее, следует в некоторых случаях отличать жидкости от газов. · Основное отличие заключается в том, что газ легко сжимается и в нём скорость распространения звука (а следовательно и всех механических возмущений) значительно меньше, чем в жидкости. Эта особенность газа должна учитываться, когда скорость движения (или скорость движения в нём твёрдого тела) становится соизмеримой со скоростью звука или превышает её. · В отличие от газа жидкость имеет граничную поверхность между ней и окружающим её газом, которая называется свободной поверхностью. В поле сил тяжести свободная поверхность жидкости имеет горизонтальный профиль. В условиях невесомости, благодаря поверхностному натяжению, свободная поверхность сферична. Это свойство жидкости, как и её малая сжимаемость, обусловлено постоянным взаимодействием соседних молекул. В газе молекулы взаимодействуют друг с другом только в момент столкновения, большую часть времени они свободно движутся в пространстве, поэтому вследствие хаотичности движения газ стремится равномерно распределиться по всей замкнутой части пространства. Если пространство не замкнуто, то объём газа может неограниченно возрастать. · В газе можно неограниченно уменьшать давление и повышать температуру, и при этом свойства газа будут меняться непрерывно. В жидкости давление может уменьшаться до некоторого значения, ниже которого начинается образование внутри неё газовых пузырьков, и начинаются фазовые переходы, которые качественно меняют свойства текучей среды. То же самое может происходить и при повышении температуры жидкости. Вязкость жидкостей и газов. Реологические свойства жидкостей. Вязкостью называется свойство текучей среды, которое заключается в возникновении в ней внутренних сил, препятствующих её деформации, т.е. изменению относительного положения её частей. Рассмотрим частный случай молекулярно-кинетической теории идеального газа - простое сдвиговое течение (рис.1.3).
Элементарная площадка · упорядоченном (продольном) со скоростью u х или uх + Duх в зависимости от того, в каком слое они находятся; · хаотическом, неупорядоченном (в том числе и поперечном) тепловом движении, скорость которого обычно на два порядка выше скорости упорядоченного движения. Вязкость газа обусловлена переносом молекулами при их тепловом движении через элементарную площадку Вводя модель сплошной среды (т.е. исключая из рассмотрения молекулярное строение вещества), считают, что на площадке
где h - динамический коэффициент вязкости, или просто динамическая вязкость газа. Это гидродинамическая характеристика, определяемая физическими свойствами текучей среды. Знак напряжения таков, как будто оно "пытается" уменьшить разность скоростей слоев. С увеличением температуры скорость хаотического движения молекул возрастает, что приводит к увеличению количества молекул, пересекающих в единицу времени площадку В жидкости основной причиной воздействия одного слоя на другой (т.е. переноса количества движения) является взаимодействие молекул, расположенных по разные стороны границы между слоями, а не перенос молекул через эту границу. Как уже отмечалось, молекулярно-кинетическая теория жидкости еще недостаточно развита, поэтому механизм вязкости в жидкости изучен значительно хуже, чем в газах. Обычно считают, что в жидкости непрерывно образуются и разрушаются при относительном скольжении слоев квазикристаллические структуры, а силы, необходимые для их разрушения, и обусловливают вязкость. Естественно, с увеличением температуры молекулы жидкости становятся более подвижными и разрушение структур происходит при меньших значениях сдвигающих сил. Таким образом, динамический коэффициент вязкости жидкости с увеличением температуры уменьшается (в отличие от газов - см. выше). Несмотря на различный молекулярный механизм возникновения напряжений в жидкостях и в газах, в обеих этих средах касательные напряжения связывают с изменчивостью поля скорости одной и той же зависи- мостью (1.3.6), которая называется законом Ньютона для вязких напряжений. В отличие от закона для сухого трения сдвиговое касательное напряжение в жидкостях и газах не зависит от нормального напряжения. Согласно определению (1.3.6) динамический коэффициент вязкости h имеет следующую единицу измерения:
Размерность h выражается через размерности напряжения Па и времени с. Иногда в качестве единицы h используют г/см×с, которая называется пуаз (в честь французского врача А. Пуазейля, выполнившего фундаментальные исследования движения вязкой жидкости) и обозначается П: Па×с = 10×П. Зависимость (1.3.6) характеризует перенос поперек потока количества движения слоев текучей среды, которое пропорционально как скорости uх, так и плотности текучей среды r. Имея это в виду, закон Ньютона целесообразно представить в форме
где
Эта величина имеет размерность
Ввиду того, что в размерность n входят только метры и секунды (и не входит размерность массы), эту величину называют кинематическим коэффициентом вязкости (или кинематической вязкостью). Размерность см2/с называется стокс (в честь английского гидромеханика Дж. Стокса, который сформулировал дифференциальные уравнения движения вязкой жидкости), и обозначается Ст: 1Ст = 10-4 м2/с. В заключение отметим, что в газах и вязкость (характеризующая перенос количества движения), и молекулярная диффузия (характеризующая перенос инородного газа) обусловлены тепловым хаотическим движением молекул. Поэтому коэффициент вязкости n имеет один порядок величины с коэффициентом молекулярной диффузии в законе Фика. В жидкостях вязкость (и связанный с этим перенос количества движения) обусловлена разрушением межмолекулярных связей, а диффузия - тепловым движением молекул, т.е. эти явления имеют различную физическую природу. Как следствие этого коэффициент диффузии в жидкости в сотни раз меньше коэффициента вязкости n.В табл. 1.1 приведены значения h, r, n для некоторых жидкостей и газов. Таблица 1.1 Значения h, r, n для некоторых жидкостей и газов
Из приведенных значений коэффициентов вязкости следует, что вязкость воды уменьшается с увеличением температуры от 0 до 100° Спочти в семь раз, а вязкость воздуха возрастает с увеличением температуры от 20 до 50°С на 25%. Для расчетов в инженерной практике пользуются ориентировочным значением кинематического коэффициента вязкости воды n = 0,01 см2/с = 0,01 Ст. Жидкости, для которых справедлива зависимость (1.3.6), называются ньютоновскими.
Однако существует много жидкостей, для которых закон Ньютона не выполняется. Наука о характере зависимости
При экспериментальном исследовании некоторых жидкостей Жидкости, поведение которых описывается кривыми 3, 4, называются жидкостями Оствальда - Вейля. Если они подчиняются зависимостям 3, то они называются псевдопластическими, а если следуют зависимости 4 - дилатантными. Механика движения таких жидкостей (это смолы, нефтепродукты, растворы полимеров и т.п.) очень сложна. СТАТИКА ТЕКУЧЕГО ТЕЛА (ГИДРОСТАТИКА) ГИДРОСТАТИЧЕСКОЕ ДАВЛЕНИЕ Гидростатика – раздел гидромеханики, в котором изучают жидкости, находящиеся в условиях равновесия (покоя). Из определения текучести физических тел следует, что в состоянии покоя в жидкости и газе касательные напряжения равны нулю, и в каждой точке, произвольно ориентированной в пространстве площадки, действуют только нормальные напряжения. Возьмем произвольную площадку (рис. 2.1, а), имеющую единичный вектор нормали
где
Сравнивая выражения (2.1.1) и (2.1.2), найдем
откуда следует, что значение нормального напряжения в фиксированной точке покоящейся жидкости не зависит от ориентации площадки. При рассмотрении напряженного состояния сплошной среды принято растягивающие напряжения считать положительными. В то же время в большинстве задач технической механики жидкости во избежание разрывов сплошности растягивающие напряжения в жидкой среде считаются недопустимыми. Это в еще большей степени относится к газообразной среде. Поэтому в гидростатике в качестве основной величины, характеризующей напряженное состояние жидкости, вводят взятое со знаком плюс нормальное напряжение (которое на всех произвольно ориентированных площадках в данной точке имеет одинаковое значение). Эта величина, являющаяся частным случаем гидродинамического давления (1.4.12), называется гидростатическим давлением и обозначается через р:
Отсюда ясно, почему в зависимости (1.4.12) стоит знак минус, определяющий величину гидродинамического давления. Матрица тензора напряжений в условиях покоя текучего тела имеет вид
Если тензорную единицу обозначить через Е, то тензор напряжения в покоящейся жидкости можно представить в виде
Таким образом, напряжённое состояние в покоящейся жидкости определяется величиной р, поэтому его характеризуют не тензором П, а считают, что оно полностью описывается величиной гидростатического давления, которое можно рассматривать как скаляр. Сила гидростатического давления
Если давление на площадке конечных размеров А (рис.2.1,б) зависит от координат, то сила давления на эту площадку определяется по формуле:
ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ РАВНОВЕСИЯ ТЕКУЧЕГО ТЕЛА (УРАВНЕНИЯ ЭЙЛЕРА) Пусть Приравняем к нулю сумму проекций на ось х всех сил, действующих на куб.
Плотность распределения массовой (объёмной) силы обозначим Поверхностные силы на грани, нормальные осям y и z, дают нулевую проекцию на ось х, так как касательные напряжения в условиях гидростатики равны нулю. В пределах куба считаем, что в разложении р(х,у,z) в ряд Тейлора можно принять в расчёт лишь члены, линейно зависящие от приращения координат. Обозначим давление на левую грань куба, перпендикулярную оси х, через р(х,у,z), при этом на правой грани давление будет равно
Приравняв нулю сумму проекций поверхностных и объемных сил на ось х, имеем:
Разделив все слагаемые на рdxdydz, получим первое уравнение равновесия. Два других уравнения выведем аналогичным образом, проектируя силы на оси у и z. В результате получим систему дифференциальных уравнений равновесия (покоя) текучего тела (уравнений гидростатики Эйлера):
Введём единичные векторы
Умножим (2.2.2) на
или
Векторное уравнение (2.2.4) равносильно системе трёх уравнений (2.2.2), где вектор gradp определяется через свои проекции на координатные оси в виде
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-01-26; просмотров: 394; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.225.72.161 (0.01 с.) |

 Рис.1.2. К определению коэффициента объёмного сжатия
Рис.1.2. К определению коэффициента объёмного сжатия
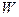 на величину Dp (рис.1.2). Сплошная среда при этом сожмётся, уменьшив свой объём на величину
на величину Dp (рис.1.2). Сплошная среда при этом сожмётся, уменьшив свой объём на величину  . Эмпирически получено, что связь между изменением объёма и давлением линейна, т.е. для каждой жидкости и газа можно ввести константу, которую называют коэффициентом объёмного расширения (при постоянной температуре):
. Эмпирически получено, что связь между изменением объёма и давлением линейна, т.е. для каждой жидкости и газа можно ввести константу, которую называют коэффициентом объёмного расширения (при постоянной температуре): . (1.3.1)
. (1.3.1) называется величина, обратная
называется величина, обратная  :
: . (1.3.2)
. (1.3.2) или
или  , (1.3.3)
, (1.3.3)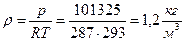 .
. (1.3.4)
(1.3.4) , (1.3.5)
, (1.3.5) - адиабатическая постоянная газа (показатель адиабаты); сv - теплоёмкость газа при постоянном объёме; ср - то же при постоянном давлении.
- адиабатическая постоянная газа (показатель адиабаты); сv - теплоёмкость газа при постоянном объёме; ср - то же при постоянном давлении. Рис.1.3. Вязкие напряжения в жидкостях и газах
Рис.1.3. Вязкие напряжения в жидкостях и газах
 поверхности, разделяющей слои 1 и 2, движется вместе с жидкостью. При этом слой жидкости 1 скользит по слою 2 с относительной скоростью
поверхности, разделяющей слои 1 и 2, движется вместе с жидкостью. При этом слой жидкости 1 скользит по слою 2 с относительной скоростью  . Молекулы газа участвуют в движениях двух видов:
. Молекулы газа участвуют в движениях двух видов: (1.3.6)
(1.3.6) .
. ,
, . (1.3.7)
. (1.3.7) .
.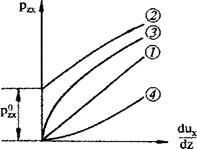 Рис. 1.4. Реологические законы в жидкостях:
1 - ньютоновская жидкость;
2 - бингамовский пластик;
3 - псевдопластическая жидкость;
4 - дилатантная жидкость.
Рис. 1.4. Реологические законы в жидкостях:
1 - ньютоновская жидкость;
2 - бингамовский пластик;
3 - псевдопластическая жидкость;
4 - дилатантная жидкость.
 называется реологией (греч. reo - течь, logos - учение). Если представить зависимость (1.3.6) в виде графика (рис.1.4), то она будет иметь вид прямой линии 1.
называется реологией (греч. reo - течь, logos - учение). Если представить зависимость (1.3.6) в виде графика (рис.1.4), то она будет иметь вид прямой линии 1. может иметь вид кривой 2. Такие жидкости, которые сопротивляются небольшим (
может иметь вид кривой 2. Такие жидкости, которые сопротивляются небольшим ( ) сдвигающим напряжениям, как твердое тело, а при (
) сдвигающим напряжениям, как твердое тело, а при ( ) ведут себя как жидкие тела, называются жидкостями Бингама - Шведова.
) ведут себя как жидкие тела, называются жидкостями Бингама - Шведова. . Поскольку вектор напряжений на этой площадке
. Поскольку вектор напряжений на этой площадке  параллелен
параллелен  , то можно записать
, то можно записать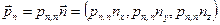 , (2.1.1)
, (2.1.1) – проекция
– проекция  на нормаль к площадке; очевидно,
на нормаль к площадке; очевидно,  . С другой стороны имеем
. С другой стороны имеем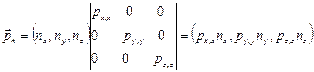 . (2.1.2)
. (2.1.2) , (2.1.3)
, (2.1.3) Рис. 2.1. Гидростатическое давление:
а - в точке сплошной среды;
б - на поверхности произвольной формы
Рис. 2.1. Гидростатическое давление:
а - в точке сплошной среды;
б - на поверхности произвольной формы
 . (2.1.4)
. (2.1.4) . (2.1.5)
. (2.1.5) (2.1.6)
(2.1.6) (рис.2.1,б), действующая на малую площадку
(рис.2.1,б), действующая на малую площадку  , – это вектор, направленный со стороны жидкости по нормали к этой площадке (такая нормаль обычно называется внутренней и её вектор равен
, – это вектор, направленный со стороны жидкости по нормали к этой площадке (такая нормаль обычно называется внутренней и её вектор равен  :
: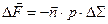 . (2.1.7)
. (2.1.7) . (2.1.8)
. (2.1.8) - давление в жидкости. Выделим внутри жидкости куб с бесконечно малыми рёбрами dx, dy, dz и рассмотрим его равновесие под действием объёмных и поверхностных сил (рис.2.2).
- давление в жидкости. Выделим внутри жидкости куб с бесконечно малыми рёбрами dx, dy, dz и рассмотрим его равновесие под действием объёмных и поверхностных сил (рис.2.2). Рис. 2.2. К выводу дифференциальных уравнений равновесия текучего тела
Рис. 2.2. К выводу дифференциальных уравнений равновесия текучего тела
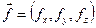 , тогда объёмная сила, действующая на куб, будет иметь проекцию на ось х, равную
, тогда объёмная сила, действующая на куб, будет иметь проекцию на ось х, равную  .
.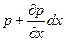 . Если считать эти грани элементарными площадками в отношении давления, то проекция на ось х силы давления на левую грань равна рdydz, а на правую равна
. Если считать эти грани элементарными площадками в отношении давления, то проекция на ось х силы давления на левую грань равна рdydz, а на правую равна 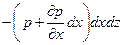 . Сумма проекций всех поверхностных сил на ось х при этом окажется равной
. Сумма проекций всех поверхностных сил на ось х при этом окажется равной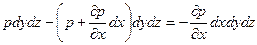 .
. . (2.2.1)
. (2.2.1) (2.2.2)
(2.2.2)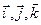 , соответствующие координатным осям х, у, z:
, соответствующие координатным осям х, у, z: . (2.2.3)
. (2.2.3)
 . (2.2.4)
. (2.2.4) (2.2.5)
(2.2.5)


