
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Введение в механику сплошной средыСтр 1 из 28Следующая ⇒
ВВЕДЕНИЕ В МЕХАНИКУ СПЛОШНОЙ СРЕДЫ СТАТИКА ТЕКУЧЕГО ТЕЛА (ГИДРОСТАТИКА) ГИДРОСТАТИЧЕСКОЕ ДАВЛЕНИЕ Гидростатика – раздел гидромеханики, в котором изучают жидкости, находящиеся в условиях равновесия (покоя). Из определения текучести физических тел следует, что в состоянии покоя в жидкости и газе касательные напряжения равны нулю, и в каждой точке, произвольно ориентированной в пространстве площадки, действуют только нормальные напряжения. Возьмем произвольную площадку (рис. 2.1, а), имеющую единичный вектор нормали
где
Сравнивая выражения (2.1.1) и (2.1.2), найдем
откуда следует, что значение нормального напряжения в фиксированной точке покоящейся жидкости не зависит от ориентации площадки. При рассмотрении напряженного состояния сплошной среды принято растягивающие напряжения считать положительными. В то же время в большинстве задач технической механики жидкости во избежание разрывов сплошности растягивающие напряжения в жидкой среде считаются недопустимыми. Это в еще большей степени относится к газообразной среде. Поэтому в гидростатике в качестве основной величины, характеризующей напряженное состояние жидкости, вводят взятое со знаком плюс нормальное напряжение (которое на всех произвольно ориентированных площадках в данной точке имеет одинаковое значение). Эта величина, являющаяся частным случаем гидродинамического давления (1.4.12), называется гидростатическим давлением и обозначается через р:
Отсюда ясно, почему в зависимости (1.4.12) стоит знак минус, определяющий величину гидродинамического давления. Матрица тензора напряжений в условиях покоя текучего тела имеет вид
Если тензорную единицу обозначить через Е, то тензор напряжения в покоящейся жидкости можно представить в виде
Таким образом, напряжённое состояние в покоящейся жидкости определяется величиной р, поэтому его характеризуют не тензором П, а считают, что оно полностью описывается величиной гидростатического давления, которое можно рассматривать как скаляр.
Сила гидростатического давления
Если давление на площадке конечных размеров А (рис.2.1,б) зависит от координат, то сила давления на эту площадку определяется по формуле:
ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ РАВНОВЕСИЯ ТЕКУЧЕГО ТЕЛА (УРАВНЕНИЯ ЭЙЛЕРА) Пусть Приравняем к нулю сумму проекций на ось х всех сил, действующих на куб.
Плотность распределения массовой (объёмной) силы обозначим Поверхностные силы на грани, нормальные осям y и z, дают нулевую проекцию на ось х, так как касательные напряжения в условиях гидростатики равны нулю. В пределах куба считаем, что в разложении р(х,у,z) в ряд Тейлора можно принять в расчёт лишь члены, линейно зависящие от приращения координат. Обозначим давление на левую грань куба, перпендикулярную оси х, через р(х,у,z), при этом на правой грани давление будет равно
Приравняв нулю сумму проекций поверхностных и объемных сил на ось х, имеем:
Разделив все слагаемые на рdxdydz, получим первое уравнение равновесия. Два других уравнения выведем аналогичным образом, проектируя силы на оси у и z. В результате получим систему дифференциальных уравнений равновесия (покоя) текучего тела (уравнений гидростатики Эйлера):
Введём единичные векторы
Умножим (2.2.2) на
или
Векторное уравнение (2.2.4) равносильно системе трёх уравнений (2.2.2), где вектор gradp определяется через свои проекции на координатные оси в виде
КИНЕМАТИКА СПЛОШНОЙ СРЕДЫ Задача кинематики - описание движения среды независимо от внешних условий, которые инициируют и поддерживают движение. Т.к. сплошная среда представляет собой непрерывную совокупность точек, то чтобы описать её движение, необходимо описать движение всех точек. Поэтому вернёмся к некоторым понятиям теоретической механики, изучающей движение точки. ПОЛЯ В ГИДРОДИНАМИКЕ При изучении движения жидкости рассматривают её как сплошную среду. Таким образом, рассматривают не движение конечного числа отдельных частиц, а поля различных физических величин: скорости, плотности, давления и т.д. Такие поля можно назвать материальными полями. Математически эти поля описывают системой функций от координат и времени. Такой подход типичен не только для механики сплошных сред, но и для ряда других областей физики. В общем случае поле является пространственным (трёхмерным), иногда задачу упрощают, и рассматривают двумерные (плоские) или одномерные поля. В этом случае полагают, что физические величины зависят от одной или двух пространственных координат. Если физические величины не зависят от времени, то поле называют стационарным, в противном случае - нестационарным. При математическом описании полей предполагают, что существуют пределы значений физических величин в точке. Такой подход упрощает физическую реальность, так как не учитывает дискретность строения материи, но такая абстракция оправдана, нужно только разумно ограничивать область полученных результатов. Так как в практических задачах размеры обтекаемых тел намного порядков больше молекулярных размеров, то в этих задачах жидкость можно рассматривать как сплошную среду. Скалярным называют поле, которое в каждой точке пространства характеризуют одним числом. Скалярное поле описывают одной функцией, зависящей от трёх координат. (Например, поле плотности или температуры). Основное свойство скалярной функции а(х1,х2,х3) состоит в том, что её численное значение не меняется при преобразовании координат. Если перейти от старой х1,х2,х3 к новой х¢1,х¢2,х¢3 системе координат, то значения плотности или температуры в фиксированной точке пространства, естественно, не изменяются: а (х¢1,х¢2,х¢3) = а (х1,х2,х3). Векторным называют поле, которое в каждой точке пространства характеризуется величиной и направлением. Например, поле скоростей жидкости. Вектор а1(х1,х2,х3), а2(х1,х2,х3), а3(х1,х2,х3), то есть, тремя функциями от трёх переменных. Это можно записать в виде матрицы-столбца:
а ÜÞ Введём новую декартову систему координат с тем же началом, но с другим направлением осей. Пусть l ij - направляющий косинус оси x¢j относительно оси xi (i = 1,2,3; j = 1,2,3). Вычислим проекции того же вектора на новые оси координат:
a¢1 = l 11 a1 + l 21 a2 + l3 1 a3; a¢2 = l 21 a1 + l 22 a2 + l23 a3; a¢3 = l 31 a1 + l 32 a2 + l33 a3. Следовательно, вектор подчиняется определённому закону преобразования его компоненти отличается от скалярной величины, численное значение которой не меняется при преобразовании координат.
То есть,сам вектор не меняется в новых координатах, а меняются его компоненты. Это выражение можно представить в индексной форме записи как сумму:
Или ещё более короткой При такой записи пользуются двумя правилами: 1. Соглашение о суммировании. По индексу, встречающемуся дважды (немой индекс), производят суммирование от 1 до 3. 2. Соглашение о ранге. Индекс, встречающийся один раз (свободный индекс), пробегает значения от 1 до 3. Таким образом, уравнение с одним свободным индексом означает запись трёх уравнений. Помимо скалярных и векторных полей в механике сплошной среды рассматриваются ещё и тензорные поля. Многие задачи физики и механики сплошной среды приводят к понятию тензора. Тензор, хотя и является обобщением понятия вектора, имеет гораздо более сложный характер. Разница заключается в том, что вектор просто интерпретируется геометрически, у тензора такого наглядного представления не существует. Описание происходит в прямолинейных (декартовых) системах координат. Координаты обозначаем х1, х2, х3, единичные векторы по осям - i1,i2, i3. Предположим, что в результате вращения осей координат как единого целого вокруг начала координат, мы перешли к новой системе координат Ox1´x2´x3´. Обозначим косинус угла между осями xi и x´k старой и новой системы aik = cos (x´i^xk). Для удобства пользования дальнейшими формулами приводим таблицу. Таблица 3.1
Теперь перейдём к определению тензора. Пусть каждому направлению Направлениям осей соответствуют векторы
Если векторы
то множество векторов Обозначим векторы, определяемые тензором для направлений новых осей
Эти условия равносильны (2.6.2) и их можно взять за новое определение тензора, если для каждой системы координат имеется тройка векторов Аналогичное определение можно дать и для вектора, если в уравнении (2.6.3) заменить векторы на проекции вектора. Поэтому тензор является обобщением вектора. Формулы (2.6.3) можно записать в сокращённом виде
Тензор определяется векторами
Из (2.6.1) и (2.6.3) можно получить формулы преобразования компонент тензора при переходе к новой системе координат:
где t´kl – компоненты в новой системе. Эти формулы можно также взять за определение тензора. Простейшими примерами являются нулевой и единичный тензоры. Согласно (2.6.4) у нулевого тензора в любой системе координат компоненты равны 0.
Для того, чтобы в дальнейшем не испытывать трудностей при использовании тензоров, запишем некоторые математические правила. ОПЕРАЦИИ НАД ТЕНЗОРАМИ
1. Умножение тензора на скаляр есть новый тензор, все компоненты которого умножены на этот скаляр (шаровой тензор):
2. Сумма тензоров есть новый тензор с компонентами, являющимися суммой одноимённых компонент слагающих тензоров. Так доля Т = Т´ + T´´ должна быть tik = t´ik + t´´ik. То, что такая сумма есть тензор, следует из линейности формул (4*). 3. Тензор, обладающий свойством tik = tki, называется симметричным. Если таблицу компонент такого тензора «повернуть» вокруг главной диагонали (то же, что и у определителя), то получится тот же самый тензор. 4. Пусть имеется тензор Т с компонентами tik.Составим таблицу с компонентами tki (т.е. повёрнутую вокруг главной диагонали). Можно показать, что она также определяет тензор, который называется сопряжённым и обозначается Т*. Очевидно, что (T*)* = T. 5. Тензор, у которого tik = - tki, называется антисимметричным. Из определения следует, что tii = - tii, т.е. tii = 0 – компоненты главной диагонали равны 0. Антисимметричный тензор всегда можно записать в виде 6. Всякий тензор можно разложить на сумму симметричного и антисимметричного тензоров: Т = ½ (Т + Т*) + ½ (Т - Т*). Легко проверить, что в первой скобке стоит симметричный, а во второй – антисимметричный тензор. 7. Пусть дан тензор Т и вектор
8. Скалярное произведение тензора Т на вектор
9. Из приведённых определений операций ясно, что они должны обладать ассоциативностью и дистрибутивностью, т.е., например,
(Т1 + Т2 ( (l
Но коммутативностью эти операции не обладают, т.е. в общем случае ( 10. Пусть даны тензоры А, В с компонентами aik и bik. Скалярное произведение тензора А на тензор В (А, В)есть новый тензор Т, компоненты которого вычисляются по формулам:
Это определение совпадает с определением матричного умножения. Компонент tik получается умножением строки с номером i тензора А на столбец с номером j тензора В. Например, t23 = а21b13 + а22 b23 + а23 b33. 11. Скалярное произведение тензоров не обладает свойством коммутативности, т.е. вообще говоря, (А,В) ¹ (В,А). Перечислим некоторые свойства, которыми оно обладает:
(lА,В) = (А,lВ) = l (А,В); (l - скаляр); (А1 + А2, В) = (А1,В)+ (А2,В); (А,В1 + В2) = (А,В1) + (А,В2); [(А,В), С) = (А,(В,С)].
УПРУГОСТЬ И ИЗГИБ УПРУГИЕ ТЕЛА Как уже отмечалось выше, при деформациях возникают внутренние напряжения, силы которых, в общем случае, зависят не только от деформаций, но и от скоростей, с которыми эти деформации происходят. В этом легко убедиться, если взять полимерное вещество, которое при обычных условиях медленно растекается подобно замазке, принимая форму сосуда, в котором оно находится. Можно без особых усилий изменить его форму, если делать это медленно. Если вылепить шарик, то легко обнаружить, что такой шарик обладает хорошими упругими свойствами, подскакивая практически после удара об пол на ту же высоту, с которой он был брошен без начальной скорости. Этот опыт показывает, что силы деформации, подобно силам вязкого трения, возрастают по мере увеличения скорости деформации. В ряде практически важных случаев силы напряжения определяются только деформациями. Такие тела, в которых это имеет место, называются абсолютно упругими телами, или упругими телами. Замечательным свойством таких тел является способность полностью восстанавливать свою форму после снятия внешних усилий, прикладываемых к телу. Рассмотрим, например, растяжение (или сжатие) стержня (рис. 4.4) с силой F, приложенной перпендикулярно к торцевой грани с площадью сечения S. Опыт показывает, что при последовательном возрастании нагрузки вначале деформации развиваются равномерно по длине стержня и растут пропорционально нагрузке, т.е.
Величина
Опыт показывает, что этот закон выполняется лишь в определенном интервале напряжений. Если растягивать стержень, последовательно увеличивая от нуля возрастающую силу, то каждый раз, после снятия нагрузки, деформация исчезает. При некотором напряжении s ³ s у появляется заметное остаточное удлинение. Это напряжение s y называется пределом упругости. На (рис.5.1) изображена зависимость деформаций от напряжений, называемая диаграммой растяжений. Следует отметить, что закон Гука выполняется только в части области упругости - области пропорциональности, когда
При возрастании нагрузки наблюдается явление текучести, т.е. внезапный рост удлинения образца при постоянной нагрузке sт, называемой пределом текучести. Отметим, что течение материала происходит равномерно по всей длине стержня. За пределами области текучести дальнейшее удлинение стержня сопровождается увеличением s. Деформации будут распределены уже неодинаково по длине стержня (рис. 5.2) - в некотором месте можно заметить образование шейки. При напряжении sм, называемом пределом прочности, в этом ослабленном сечении происходит разрыв. То напряжение, которое данный материал может выдержать на практике, не разрушаясь и не получая опасной деформации, называют допустимым и обозначают [s]. Обычно [s] < sп, и все расчеты проводят на основе законов Гука. Чтобы обеспечить прочность при всех обстоятельствах допустимое напряжение выбирается как часть предела прочности, в частности, для металлов [s] = 0.2sм, а для дерева[s] = 0.1sм. Следует отметить, что наибольшие деформации, которые может выдержать материал, не определяются протяженностью области текучести. Если область текучести велика, то материал называется пластичным. Такой материал, как например сталь, способен выдерживать большие нагрузки без разрушения. Наоборот, если область текучести невелика, то этот материал хрупок. Хрупкие материалы, как чугун например, разрушаются при деформациях e ³ eп. В ряде случаев пластичные материалы могут разрушаться и при малых деформациях e» eп (например, сталь при температуре ниже - 45°С). Аналогичными свойствами обладают и сдвиговые деформации. В частности, в области пропорциональности связь между деформациями сдвига и касательным напряжением (рис.4.9) задается соотношением
в котором Таблица 5.1 Характеристики упругости и прочности некоторых материалов
Из этой таблицы можно сделать два важных вывода. Во-первых, поскольку предел пропорциональности sп на 2 ¸ 3 порядка меньше модуля упругости, то в области упругости деформации eу < 10-3 ¸10-2. Во-вторых, просматривается связь между величиной модуля Юнга E и модуля сдвига G - чем больше E, тем больше и G. Это не случайно, т.к. между обеими величинами существует жесткая связь. Чтобы ее установить, рассмотрим растяжение маленького кубика с длиной стороны
Обратим внимание на то, что квадратная грань ABCD параллелепипеда, находящегося внутри рассматриваемого кубика, превращается при деформациях в ромбическую грань A'B'C'D'. Совершенно ясно, что параллелепипед испытывает сдвиговую деформацию, а его объем при этом практически не изменился (см. также формулу (5.1.17)). Величину угла сдвига a можно легко связать с деформацией удлинения
Поскольку b << 1, то
Приравнивая правые части (5.1.4) и (5.1.5), находим
Сила F, растягивающая кубик (рис. 5.4), создает нормальное напряжение
Поскольку деформации e в формуле (5.1.6) пропорциональны напряжениям, a s = 2sт, то
Сравнивая последнее равенство с соотношением (5.1.3), при учете, что,
В рассмотренном примере следует обратить внимание на то, что величина и направление силы, приложенной к некоторой площадке, зависит от ориентации и величины этой площадки. Так, на грань Посмотрим, что будет происходить с тем же кубиком, если его растягивать одновременно силами, приложенными ко всем его граням. В этом случае относительные удлинения каждой из его сторон будут задаваться соотношениями:
Формулы (5.1.10) описывают деформации кубика при его всестороннем растяжении или сжатии. Если напряжения одинаковы, (s1 = s2 = s3 = s), то деформации также будут одинаковы: (e1 = e2 = e3 = e) и
Параметр
называется модулем всестороннего сжатия и играет важную роль в теории упругости. Важно отметить, что хрупкие материалы, подвергнутые всестороннему давлению, на которое дополнительно накладывается растяжение, сжатие или сдвиг, обнаруживают значительные пластические деформации. Такие деформации играют существенную роль, например, в процессах образования рельефа земной коры: граниты и базальты, хрупкие в обычных условиях, текут под действием колоссального давления в глубинных слоях Земли. Деформации растяжения и сдвига возникают в практически важных случаях изгибов балок строительных конструкций и окруживания валов машин и механизмов.
УПРУГИЕ ДЕФОРМАЦИИ Упругими деформациями называются такие, которые после снятия приложенных напряжений исчезают. Материалы, в которых при данных напряжениях возникают упругие деформации, называются упругими материалами. Почти все твёрдые тела (горные породы) при относительно низких температурах и давлениях и не слишком высоких напряжениях являются упругими. Упругие деформации в твёрдых телах прямо пропорциональны приложенным напряжениям. Изотропными материалами называются такие, у которых упругие свойства не зависят от направления. При высоких уровнях напряжений и температур в породах проявляются отклонения от упругого поведения. При низких температурах и всесторонних давлениях породы проявляют хрупкие свойства и при значительных девиаторных напряжениях разрушаются. В недрах Земли, где всестороннее давление растёт с глубиной и когда оно достигает предела хрупкого разрушения, в породе возникают пластические деформации. Пластическими называют непрерывные, необратимые деформации, происходящие без разрушения. При этом, после того как действие силы, вызывающей пластическую деформацию, прекращается, деформация частично сохраняется (не исчезает полностью).
ОСНОВЫ ГИДРОДИНАМИКИ ОСНОВНЫЕ ПОЛОЖЕНИЯ Задачи гидродинамики делятся на два основных класса: внутренние и внешние. К внешним задачам относятся задачи обтекания тела потоками жидкости или газа, или о движении тела в жидкой или газообразной среде. Внешними задачами являются задачи, связанные с полётами самолётов, снарядов и других тел, движущихся в атмосфере. Внутренние задачи занимаются движением жидкости в каналах. В этот класс задач входят такие, как: 1. течение жидкостей в трубопроводах (водопровод, газо-и нефтепроводы, кровеносная система, тепло и газоснабжение); 2. течение воды в открытых каналах и реках (ирригационные и осушительные системы, расчёт паводков, судопропускные сооружения и т.д.). При решении внешней задачи основной акцент делается на определение силового взаимодействия потока и тела. Определение силы, действующей со стороны набегающего потока, или силы сопротивления движению тела в жидкости - цель таких задач. Поэтому при анализе и решении внешних задач, как правило, используются уравнения, выражающие закон изменения количества движения: дифференциальные уравнения Навье - Стокса или Рейнольдса, а также интегральные формы этого закона. При решении внутренней задачи чаще всего стараются определить потери энергии в потоке жидкости. Здесь используются уравнения, выражающие закон изменения энергии, чаще всего в виде различных форм уравнения Бернулли. В основе гидродинамики, как части гидромеханики, положены три основных закона механики: I. закон сохранения массы; II. закон сохранения количества движения (импульса); III. закон сохранения энергии. Эти законы формулируются для конечных объёмов (размеры ограничены и оговорены). В МСС используются два подхода к описанию движения сплошной среды: Лагранжев и Эйлеров. Соответственно при Лагранжевом подходе используется движующиеся (материальные, индивидуальные) объемы Законы гидродинамики для конечных объёмов часто упрощаются с учётом конкретных условий на поверхностях, ограничивающих данный объём. Такие упрощенные уравнения используются в разделе, называемом гидравликой. По сути, это теоретические основы технической механики жидкости. Они особенно эффективны, когда исследуются интегральные (осреднённые по времени и пространству) гидромеханические характеристики потоков. В том случае, когда есть необходимость определять гидромеханические характеристики и величины в каждой точке объёма жидкости, используют дифференциальные уравнения. Они тоже являются фундаментальными законами механики, но относятся к точке сплошной среды. Если эти уравнения дополнить каким-либо реологическим законом, то можно определить структуру поля скорости и напряжённое состояние в любой точке потока жидкости. Практическое использование этих уравнений, в зависимости от изложенных здесь подходов, преобразуется из одного вида в другой с помощью теоремы Остроградского - Гаусса. Так при выводе гидравлических уравнений объёмные интегралы заменяются на поверхностные с тем, чтобы использовать особенности условий на поверхностях, ограничивающих поток, для упрощения уравнений. При выводе дифференциальных уравнений, наоборот, поверхностные интегралы заменяются на объёмные, чтобы можно было исследовать гидромеханические величины в точках внутри потока. При этом условия на границах потока вводятся как граничные или краевые условия для дифференциальных уравнений.
ЗАКОН СОХРАНЕНИЯ МАССЫ Выделим в пространстве контрольный материальный объём Масса бесконечно малого объёма
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-01-26; просмотров: 420; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.224.32.40 (0.133 с.) |
 . Поскольку вектор напряжений на этой площадке
. Поскольку вектор напряжений на этой площадке  параллелен
параллелен  , то можно записать
, то можно записать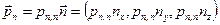 , (2.1.1)
, (2.1.1) – проекция
– проекция  на нормаль к площадке; очевидно,
на нормаль к площадке; очевидно,  . С другой стороны имеем
. С другой стороны имеем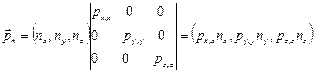 . (2.1.2)
. (2.1.2) , (2.1.3)
, (2.1.3) Рис. 2.1. Гидростатическое давление:
а - в точке сплошной среды;
б - на поверхности произвольной формы
Рис. 2.1. Гидростатическое давление:
а - в точке сплошной среды;
б - на поверхности произвольной формы
 . (2.1.4)
. (2.1.4) . (2.1.5)
. (2.1.5) (2.1.6)
(2.1.6) (рис.2.1,б), действующая на малую площадку
(рис.2.1,б), действующая на малую площадку  , – это вектор, направленный со стороны жидкости по нормали к этой площадке (такая нормаль обычно называется внутренней и её вектор равен
, – это вектор, направленный со стороны жидкости по нормали к этой площадке (такая нормаль обычно называется внутренней и её вектор равен  :
: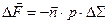 . (2.1.7)
. (2.1.7) . (2.1.8)
. (2.1.8) - давление в жидкости. Выделим внутри жидкости куб с бесконечно малыми рёбрами dx, dy, dz и рассмотрим его равновесие под действием объёмных и поверхностных сил (рис.2.2).
- давление в жидкости. Выделим внутри жидкости куб с бесконечно малыми рёбрами dx, dy, dz и рассмотрим его равновесие под действием объёмных и поверхностных сил (рис.2.2). Рис. 2.2. К выводу дифференциальных уравнений равновесия текучего тела
Рис. 2.2. К выводу дифференциальных уравнений равновесия текучего тела
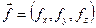 , тогда объёмная сила, действующая на куб, будет иметь проекцию на ось х, равную
, тогда объёмная сила, действующая на куб, будет иметь проекцию на ось х, равную  .
.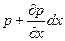 . Если считать эти грани элементарными площадками в отношении давления, то проекция на ось х силы давления на левую грань равна рdydz, а на правую равна
. Если считать эти грани элементарными площадками в отношении давления, то проекция на ось х силы давления на левую грань равна рdydz, а на правую равна 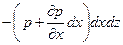 . Сумма проекций всех поверхностных сил на ось х при этом окажется равной
. Сумма проекций всех поверхностных сил на ось х при этом окажется равной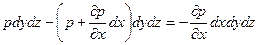 .
. . (2.2.1)
. (2.2.1) (2.2.2)
(2.2.2)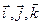 , соответствующие координатным осям х, у, z:
, соответствующие координатным осям х, у, z: . (2.2.3)
. (2.2.3)
 . (2.2.4)
. (2.2.4) (2.2.5)
(2.2.5) в пространстве трёх измерений может быть задан тремя компонентами:
в пространстве трёх измерений может быть задан тремя компонентами:

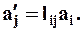
 соответствует вектор
соответствует вектор  (не обязательно коллинеарный n).
(не обязательно коллинеарный n). , разложение которых опишем подробно:
, разложение которых опишем подробно: (3.6.1)
(3.6.1) , (3.6.2)
, (3.6.2) . Подставляя в предыдущее выражение (2.6.2) вместо
. Подставляя в предыдущее выражение (2.6.2) вместо  (3.6.3)
(3.6.3) , преобразующаяся по формулам (2.6.3) в тройку
, преобразующаяся по формулам (2.6.3) в тройку  , отвечающую другой системе координат, то этим определяется тензор.
, отвечающую другой системе координат, то этим определяется тензор. .
. .
.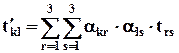 , (3.6.4)
, (3.6.4) .
. .
. .
. .Скалярное произведение тензора Т на вектор
.Скалярное произведение тензора Т на вектор  справа есть новый вектор
справа есть новый вектор  , обозначаемый (Т,
, обозначаемый (Т,  (i = 1,2,3).
(i = 1,2,3). , обозначаемый (
, обозначаемый (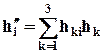 .
. .
. . (5.1.1)
. (5.1.1) называется нормальным напряжением в торцевом сечении стержня. Пропорциональность деформаций e соответствующим напряжениям выражает закон Гука. Коэффициент пропорциональности c называется коэффициентом удлинения и для каждого материала определяется опытным путем. Так как численные значения e гораздо меньше e, то c - весьма малая величина. Поэтому обычно вводят модуль упругости (модуль Юнга) Е = c-1, и закон Гука окончательно записывают в виде
называется нормальным напряжением в торцевом сечении стержня. Пропорциональность деформаций e соответствующим напряжениям выражает закон Гука. Коэффициент пропорциональности c называется коэффициентом удлинения и для каждого материала определяется опытным путем. Так как численные значения e гораздо меньше e, то c - весьма малая величина. Поэтому обычно вводят модуль упругости (модуль Юнга) Е = c-1, и закон Гука окончательно записывают в виде Рис.5.1. Диаграмма растяжения
Рис.5.1. Диаграмма растяжения
 . (5.1.2)
. (5.1.2) .
. Рис.5.2. Образование шейки
Рис.5.2. Образование шейки
 , (5.1.3)
, (5.1.3) - касательное напряжение, аналогичное по смыслу введенному выше нормальному напряжению, а G - модуль сдвига, являющийся, как и модуль Юнга, также характеристикой материала.
- касательное напряжение, аналогичное по смыслу введенному выше нормальному напряжению, а G - модуль сдвига, являющийся, как и модуль Юнга, также характеристикой материала. , как это было изображено на рис. 5.3.
, как это было изображено на рис. 5.3. Рис.5.3. Растяжение кубика (связь между модулем Юнга и модулем сдвига)
Рис.5.3. Растяжение кубика (связь между модулем Юнга и модулем сдвига)
 и коэффициентом Пуассона
и коэффициентом Пуассона  . Из треугольника A'OD' следует, что
. Из треугольника A'OD' следует, что . (5.1.4)
. (5.1.4) . (5.1.5)
. (5.1.5) . (5.1.6)
. (5.1.6) Рис. 5.4. Взаимосвязь сил и
напряжений, действующих на грани кубика
Рис. 5.4. Взаимосвязь сил и
напряжений, действующих на грани кубика
 . Это напряжение передается на грани AB и BC параллелепипеда, но силы, действующие на каждую из его граней, имеют не только нормальную к грани, но и направленную вдоль грани параллельную составляющую Fт. Касательное напряжение оказывается при этом равным
. Это напряжение передается на грани AB и BC параллелепипеда, но силы, действующие на каждую из его граней, имеют не только нормальную к грани, но и направленную вдоль грани параллельную составляющую Fт. Касательное напряжение оказывается при этом равным . (5.1.7)
. (5.1.7) . (5.1.8)
. (5.1.8) , находим искомую связь между модулями Юнга и сдвига:
, находим искомую связь между модулями Юнга и сдвига: . (5.1.9)
. (5.1.9) куба действует сила F, перпендикулярная к грани, в то время как на грань параллелепипеда
куба действует сила F, перпендикулярная к грани, в то время как на грань параллелепипеда  (5.1.10)
(5.1.10) . В результате всесторонней деформации новый объем кубика станет равным
. В результате всесторонней деформации новый объем кубика станет равным  , а его относительное изменение составит величину
, а его относительное изменение составит величину . (5.1.11)
. (5.1.11) (5.1.12)
(5.1.12) , состоящая при всех t из одних и тех же частиц, граница которых
, состоящая при всех t из одних и тех же частиц, граница которых  непроницаема. При втором подходе – неподвижные объемы
непроницаема. При втором подходе – неподвижные объемы  с проницаемой границей
с проницаемой границей  . Далее будем использовать первый подход.
. Далее будем использовать первый подход. - плотность.
- плотность. , в момент времени t равна
, в момент времени t равна  . Масса объёма
. Масса объёма  . (6.2.1)
. (6.2.1)


