
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Течение ньютоновской жидкости в круглой трубеСодержание книги
Поиск на нашем сайте
Рассмотрим ламинарное течение вязкой (ньютоновской) жидкости в круглой трубе радиуса R. При таком течении цилиндрические слои жидкости (которые должны мыслиться бесконечно тонкими) перемещаются в направлении оси трубы z, совершая "телескопическое" движение (рис. 8.2, а). Так как жидкость несжимаема, то скорость Сила вязкого сопротивления, действующая на внешнюю поверхность цилиндра со стороны внешних слоев, равна
(знак "минус" означает, что сила сопротивления направлена против оси z). По закону Ньютона
Интегрируя это уравнение, получаем с учетом граничного условия
Измеряемой в опытах величиной является расход Q -объем жидкости, протекающей через поперечное сечение трубы за единицу времени, поэтому вычислим эту величину. Для этого разобьем сечение трубы на узкие кольца шириной dr. Расход жидкости через кольцо с внутренним диаметром Расход через всё сечение может быть получен простым интегрированием:
Таким образом, в случае ньютоновской жидкости наблюдается линейная связь между перепадом давления и расходом жидкости. Определив среднюю по сечению скорость как Распределение (8.2.2) было получено Стоксом (Stokes, 1849 г.) и Гагенбахом (Hagenbach, 1860 г.). Последний назвал соотношение НЕНЬЮТОНОВСКИЕ ЖИДКОСТИ Гипотеза Ньютона о линейной связи между тангенциальным напряжением и скоростью сдвига оказалась очень удобным приближением, справедливым для абсолютного большинства низкомолекулярных жидкостей, но при рассмотрении реологических свойств жидкостей, склонных к структурообразованию (суспензий, эмульсий, растворов полимеров, красок, «тяжёлых нефтей», глинистых растворов и т.д.), были обнаружены многочисленные отклонения от закона Ньютона. Такие жидкости называются неньютоновскими, и для них реологическая кривая Типичным примером неньютоновских жидкостей являются полимерные системы, в которых длинные гибкие молекулы, зацепляясь друг за друга, образуют некую пространственную структуру («сетку»), резко повышающую вязкость. Под действием сдвиговых деформаций часть структурных связей разрушается, что приводит к уменьшению вязкости. Отметим тот факт, что Пуазейль был по профессии медиком и интересовался прохождением крови через малые кровеносные сосуды. Сейчас известно, что кровь не является ньютоновской жидкостью, поэтому автор опыта, экспериментально подтвердившего на примере воды предположения Ньютона, в каком-то смысле является первым исследователем неньютоновских сред.
|
|||||
|
Последнее изменение этой страницы: 2017-01-26; просмотров: 273; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.191.165.149 (0.007 с.) |

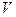 остается постоянной по длине трубы и зависит только от расстояния
остается постоянной по длине трубы и зависит только от расстояния  до центральной оси. Для определения зависимости
до центральной оси. Для определения зависимости  составим уравнение равновесия сил, действующих на цилиндрический объем жидкости длиной
составим уравнение равновесия сил, действующих на цилиндрический объем жидкости длиной 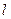 и радиусом
и радиусом 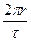 . Эта сила уравновешивается разницей сил давления, действующих на основания цилиндра, поэтому
. Эта сила уравновешивается разницей сил давления, действующих на основания цилиндра, поэтому , откуда
, откуда 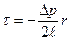 (8.2.1)
(8.2.1) Рис. 8.2. Ламинарное течение
ньютоновской жидкости в трубе
Рис. 8.2. Ламинарное течение
ньютоновской жидкости в трубе
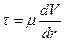 , откуда
, откуда .
.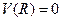 зависимость
зависимость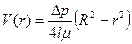 . (8.2.2)
. (8.2.2)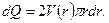
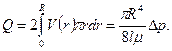 (8.2.3)
(8.2.3) получим отсюда
получим отсюда 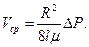
 законом Пуазейля в честь французского ученого (Poiseuille, 1797-1869), который в экспериментах с водой установил эмпирическую зависимость между расходом, геометрическими размерами тела и давлением.
законом Пуазейля в честь французского ученого (Poiseuille, 1797-1869), который в экспериментах с водой установил эмпирическую зависимость между расходом, геометрическими размерами тела и давлением.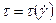 (или, как часто говорят, кривая течения) не является линейной, т.е. вязкость не остаётся постоянной, а зависит от скорости сдвига или от предыстории деформации материала.
(или, как часто говорят, кривая течения) не является линейной, т.е. вязкость не остаётся постоянной, а зависит от скорости сдвига или от предыстории деформации материала.


