
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Определение эффективного диаметраСодержание книги
Поиск на нашем сайте
Зная закон массового распределения частиц по размерам и имея в своём распоряжении интегральную кривую весового участия фракций грунта, можно определить эффективный диаметр. · Метод Аллан Газена. За эффективный диаметр частицы принимается такой диаметр, для которого сумма весов всех фракций от нуля и, кончая этим диаметром, составляет 10% от взятого веса грунта; при этом должно выполняться условие · Метод Крюгер - Цункера. Эффективный диаметр определяется из соотношения:
где
· Метод Козени. Эффективный диаметр находится по формуле:
При этом d1 - верхний крайний диаметр последней фракции (который должен быть меньше 0.0025мм). Dg1 - доля веса грунта последней фракции, выраженная в процентах. Средний диаметр фракции
· Графический метод определения эффективного диаметра. · Метод Замарина. Эффективный диаметр определяется по формуле:
где Аi - угловые коэффициенты (относительно оси d) последовательных прямых отрезков кривой весового участия фракции. ФОРМУЛЫ ФИЛЬТРАЦИИ Закон Дарси. При очень медленном движении жидкости в пористой среде (пласте), когда силы инерции ничтожно малы и ими можно пренебречь, для скорости фильтрации принят так называемый линейный закон фильтрации, или закон Дарси:
где DH/l - потеря напора на единицу длины пласта (соответствует гидравлическому уклону i). Коэффициент пропорциональности К в формуле (2.36) называется коэффициентом фильтрации. Он характеризует одновременно фильтрационную способность среды и протекающей в нём жидкости. [К] = [см/с]. Закон Дарси можно выразить через коэффициент проницаемости k, характеризующий пористую среду, и динамический коэффициент вязкости m жидкости:
g - удельный вес жидкости. Расход жидкости Q, протекающий через площадь фильтрации f, определяется формулой:
Закон Дарси в дифференциальной форме
где s - направление, которое берётся вдоль струйки по скорости Для коэффициента проницаемости имеем
[k] = см2. 1 дарси = Коэффициент проницаемости равен 1 дарси при абсолютной вязкости m = 1 сантипуазу, Dр =1 ат на длине 1 см, площади сечения 1 см2 и расходе жидкости 1 см3/с. При движении жидкости в крупнозернистых грунтах закон ламинарной фильтрации нарушается в связи с турбулентным характером течения. Такое нарушение может происходить и при ламинарном движении за счёт сравнительно высоких скоростей течения, при которых нельзя пренебрегать влиянием сил инерции. Критерием существования ламинарной фильтрации является число Рейнольдса. · По Н.Н. Павловскому При этом 7< Reкр < 9. · По В.Н. Щелкачёву · М.Д. Миллионщиков ввёл в формулу Рейнольдса внутренний масштаб породы (линейный размер ) l*:
где k - коэффициент проницаемости, m - пористость; за характерную скорость принимается истинная скорость фильтрации, равная Тогда
Критическое значение 0.022 < Reкр < 0.290. Если фильтрация не подчиняется закону Дарси (нелинейна), то используют следующие представления: · скорость U или дебит Q представляются степенной зависимостью от градиента давления
где C и n некоторые коэффициенты; · двучленной формулой для градиента давления вида
где - Скорости фильтрации струек пропорциональны расходам (дебитам), поэтому двучленный закон сопротивления при нелинейной фильтрации может быть представлен уравнением индикаторной кривой для несжимаемой жидкости в виде
графически изображаемой параболой. Для газа (воздуха) будем иметь
где А1 и В1 - параметры, характерные для данного пласта и скважины. Ø Л.С. Лейбензон, исходя из общей теории фильтрации, предложил определять скорость фильтрации по формуле:
здесь n - кинематический коэффициент вязкости, J - гидравлический уклон, k - проницаемость, B1 - постоянная величина. При квадратичной турбулентной фильтрации показатель степени S = 2. Движение газа в пористой среде. Общее уравнение установившегося движения газа через пористую среду имеет вид
где q - функция давления, Уравнения движения газов в пористой среде нелинейны и решить их можно только в некоторых конкретных случаях при введении определённых упрощений. Рассмотрим несколько частных решений, представляющих интерес с позиций проводки нефтяных и газовых скважин и широко используемых в различных расчётах при бурении. Пусть при бурении скважины радиусом rс частично (рис. 9.1,б) или полностью (в) вскрыт проницаемый пласт кругового контура радиусом Rk, имеющий непроницаемые кровлю, подошву и толщину h (рис.9.1).
В случае применимости закона Дарси для несжимаемой жидкости справедливы следующие формулы для расчёта расхода при стационарной фильтрации. При большой мощности пласта (рис.9.1,а) имеем формулу для расчёта расхода на стенках скважины:
При этом для рk > рс скважина проявляет с дебитом Q, а в противном случае поглощает. При условии rс << h и незначительном заглублении (рис.9.1, б) формула для расчёта с удовлетворительной для инженерных расчётов точностью имеет вид
Аналогично при рk > рс имеет место проявление с дебитом Q, а в противном случае поглощение. Наконец, (рис.9.1, в) расход определяется по формуле Дюпюи:
при тех же условиях. Во всех приведённых формулах индексы «с» и «k» означают скважину и контур, а под давлением рk понимается пластовое давление. Обычно крайне трудно задаваться радиусом контура Rk. Если при его задании ошибиться в m раз, то
При условии, что Rk обычно в сотни или тысячи раз больше h или rс, первые члены будут на порядок больше вторых членов при m = 2÷3. Поэтому погрешности от ошибочного задания радиуса контура в 2-3 раза приводят к ошибкам порядка 10%. Т.е. двух и трёхкратные ошибки при задании Rk вполне допустимы. Приведённые выше формулы применены при фильтрации по закону Дарси, а во многих случаях вскрываются трещинные и порово-трещинные коллекторы, для которых справедливы законы течения, описываемые формулами Форхгеймера или Краснопольского - Шези. В случае применимости закона Краснопольского - Шези формула для расчёта расхода имеет вид
где а - постоянная характеристика фильтрации. Принимая во внимание, что rk >> rс, последнюю формулу можно записать в виде
При фильтрации по закону Форхгеймера расчётная формула для определения Q приближённо записывается в виде
где b - постоянная двухчленного закона фильтрации. Все приведённые выше формулы могут использоваться и для течения газов. В этом случае вместо разности давлений необходимо применять разность квадратов давлений, т.е.
а для случая одномерного течения соответствующая формула была приведена выше, где в отличие от формулы для жидкости появился множитель
|
|||||
|
Последнее изменение этой страницы: 2017-01-26; просмотров: 333; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.57 (0.01 с.) |

 где dе - диаметр, при котором сумма весов всех фракций от нуля и, кончая этим диаметром, составляет 60% от веса всех фракций. Это отношение называется коэффициентом неоднородности.
где dе - диаметр, при котором сумма весов всех фракций от нуля и, кончая этим диаметром, составляет 60% от веса всех фракций. Это отношение называется коэффициентом неоднородности. , (9.2.1)
, (9.2.1) - весовое участие фракции в общем весе взятой единицы объёма грунта, di - средний диаметр фракции, определяемый как среднее арифметическое крайних диаметров
- весовое участие фракции в общем весе взятой единицы объёма грунта, di - средний диаметр фракции, определяемый как среднее арифметическое крайних диаметров  и
и  этой фракции:
этой фракции: .
.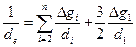 . (9.2.2)
. (9.2.2)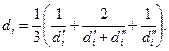
 (9.2.3)
(9.2.3) , (9.3.1)
, (9.3.1) , (9.3.2)
, (9.3.2) . (9.3.3)
. (9.3.3) , (9.3.4)
, (9.3.4) .
. (9.3.5)
(9.3.5)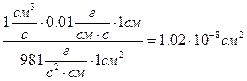 .
. .
.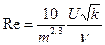 , 1< Reкр < 12.
, 1< Reкр < 12. ,
, .
.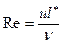 . (9.3.6)
. (9.3.6) , (9.3.7)
, (9.3.7) , (9.3.8)
, (9.3.8) - элемент струйки, b - коэффициент, зависящий от геометрии пористой среды, шероховатости и т.п.
- элемент струйки, b - коэффициент, зависящий от геометрии пористой среды, шероховатости и т.п.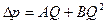 , (9.3.9)
, (9.3.9) ,
,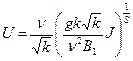 ;
;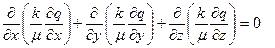 , (9.3.10)
, (9.3.10)
 Рис.9.1.Схемы вскрытия проницаемого пласта скважиной
Рис.9.1.Схемы вскрытия проницаемого пласта скважиной
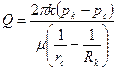 , или
, или 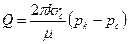 , т.к.
, т.к.  . (9.3.11)
. (9.3.11) (9.3.12)
(9.3.12) (9.3.13)
(9.3.13)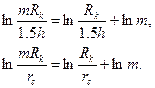
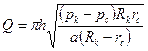 , (9.3.14)
, (9.3.14) (9.3.15)
(9.3.15)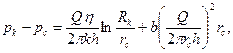 (9.3.16)
(9.3.16) а вместо объёмного расхода Q определяется приведённый к стандартным условиям (например, к пластовой температуре и атмосферному давлению) объёмный расход Qприв . Так, формула Дюпюи при течении газов имеет вид
а вместо объёмного расхода Q определяется приведённый к стандартным условиям (например, к пластовой температуре и атмосферному давлению) объёмный расход Qприв . Так, формула Дюпюи при течении газов имеет вид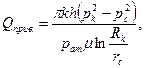 (9.3.17)
(9.3.17) (где рат - атмосферное давление).
(где рат - атмосферное давление).


