
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Поверхность уровня и ее свойстваСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Поверхностью уровня называется поверхность, все точки которой имеют одно и тоже значение рассматриваемой функции. В гидравлике особо важное значение имеет поверхность равного давления. Во всех точках такой поверхности уровня гидростатическое давление одинаково, т.е. р = const и dр = 0, поэтому из уравнения (2.13) следует
т.к. плотность жидкости ρ≠0, то
Формула (2.31) называется уравнением поверхности равного давления. Поверхность равного давления обладает двумя свойствами. 1. Две поверхности равного давления не пересекаются между собой. Допустим, что поверхность равного давления р1 пересекается с поверхностью равного давления р2. Тогда в точках линии пересечения этих поверхностей давление было бы одновременно равным и р1 и р2, что невозможно, т.к. р1≠ р2. Следовательно, поверхности равного давления не пересекаются. 2. Внешние объемные силы направлены нормально к поверхности уровня. Докажем это свойство. По второму закону Ньютона, элементарная работа сил, действующих в жидкости, равна:
Согласно формуле (2.31), имеем dA = 0. С другой стороны, из механики твердого тела известно, что
где α – угол между вектором силы и направлением движения; F – сила, действующая на единицу объема жидкости; dl – элементарный путь. Так как F ≠ 0, dl ≠ 0, dA=0, то получаем
Интегрируя выражения (2.32) получаем
Уравнения (2.33) представляют собой семейство горизонтальных плоскостей. Следовательно, поверхностью равного давления в поле сил тяжести является горизонтальная плоскость. ОТНОСИТЕЛЬНОЕ РАВНОВЕСИЕ ЖИДКОСТИ ВО ВРАЩАЮЩЕМСЯ СОСУДЕ
Относительным равновесием жидкости называется такой случай ее движения, при котором отдельные ее частицы не смещаются одна относительно другой, и вся масса жидкости движется как твердое тело.
Предположим, что цилиндр, наполненный жидкостью до высоты h, приведен во вращательное движение вокруг вертикальной оси OZ с угловой скоростью ω (рис.2.11). Рис 2.11 Вращающиеся стенки цилиндра приведут во вращение ближайшие к стенкам слои жидкости, а затем, вследствие вязкости жидкости, и всю ее массу. По истечении некоторого времени вся жидкость будет вращаться, примерно стой же угловой скоростью ω, что и сосуд. Допустим, что такой момент времени наступил. Рассмотрим два интересующих нас вопроса. 1. Какую форму будет иметь поверхность равного давления, и в частности, свободная поверхность? 2. Каков закон распределения гидростатического давления? Чтобы ответить на поставленные вопросы, рассмотрим уравнение поверхности равного давления (2.31). Для нахождения проекций ускорения выберем в жидкости точку А и покажем ускорения возникающие под действием сил, действующих в жидкости. Силами, действующими в жидкости, являются сила земного тяготения (направленная вертикально вниз по оси OZ) и центробежная сила (направленная вдоль оси ОХ к периферии). В результате действия этих сил полное ускорение точки А будет складываться из ускорения свободного падения g и центробежного ускорения ε. Составляющие массовых сил, действующих в данном случае на жидкость, X, Y, и Z будут равны:
где εх, εy – проекции центробежного ускорения по осям х и y. Подставляя выражения (2.34) в уравнение (2.31) получаем
После решения уравнения (2.35) относительно dz и его интегрирования получаем
Постоянную интегрирования С находим из следующих условий: Х = 0, Y= 0, Z = h*. Следовательно С = h*, т.е. постоянная интегрирования равна глубине залегания самой нижней точки свободной поверхности (вершины параболы). С учетом постоянной интегрирования С, и при условии, что величина h* определяется из условия неизменности первоначального объема жидкости, т.е.
уравнение (2.36) принимает вид:
Полученное уравнение (2.38) является уравнением свободной поверхности жидкости во вращающемся сосуде. Согласно полученному уравнению (2.38), формой свободной поверхности является параболоид вращения. В уравнении (2.38), x2 + y2= r2, где r – координата рассматриваемой точка А. При условии, что r = R, т.е. рассматриваемая точка А находится на внутренней поверхности вращающегося сосуда, наблюдается максимальный подъем жидкости на высоту zmax. Для определения zmax в уравнение (2.38) подставляем выражение x2 + y2= r2 и получаем
Согласно полученному уравнению (2.39) можно сделать вывод, что жидкость во вращающемся сосуде поднимается на столько, на сколько и опускается. Теперь установим закон распределения гидростатического давления. Подставляя выражения (2.34) в уравнение (2.13) получим
Выполняя интегрирования уравнения (2.40) получим
Постоянную интегрирования С находим из следующих условий: Х = 0, Y= 0, Z = h*, р=ратм. С учетом вышеперечисленного, уравнение (2.41) принимает следующий вид:
или
Уравнения (2.42) и (2.43) являются уравнениями закона распределения гидростатического давления.
|
|||||||
|
Последнее изменение этой страницы: 2017-01-26; просмотров: 2124; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.147.104.18 (0.008 с.) |

 ,
, . (2.31)
. (2.31) .
. ,
, или
или  . Если жидкость находится только в поле сил земного тяготения, то ускорения X, Y, Z вдоль координатных осей равны: X = 0, Y = 0, Z = – g. После подстановки этих значений в уравнение (2.31) имеем
. Если жидкость находится только в поле сил земного тяготения, то ускорения X, Y, Z вдоль координатных осей равны: X = 0, Y = 0, Z = – g. После подстановки этих значений в уравнение (2.31) имеем или
или 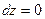 . (2.32)
. (2.32)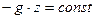 или
или  . (2.33)
. (2.33)
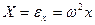 ;
;  ;
;  , (2.34)
, (2.34) . (2.35)
. (2.35)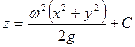 . (2.36)
. (2.36) , (2.37)
, (2.37) . (2.38)
. (2.38) . (2.39)
. (2.39) . (2.40)
. (2.40) . (2.41)
. (2.41)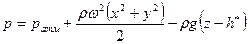 (2.42)
(2.42) . (2.43)
. (2.43)


