
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Гидравлический удар в трубах⇐ ПредыдущаяСтр 22 из 22
Гидравлическим ударом называется резкое повышение давления жидкости в трубопроводе при его внезапном перекрытии (однако могут быть и другие причины его возникновения). Точнее говоря, гидравлический удар представляет собой колебательный процесс, возникающий в упругом трубопроводе с капельной жидкостью при внезапном изменении ее скорости. Этот процесс является очень быстротечным и характеризуется чередованием резких повышений и понижений давления. Изменение давления при этом тесно связано с упругими деформациями жидкости и стенок трубопровода. В водопроводной технике явление гидравлического удара известно давно, но задача его расчета была решена сравнительно недавно (в 1898 г. профессором Н.Е.Жуковским). Для истолкования процесса гидравлического удара предположим, что в напорном трубопроводе жидкость движется со средней скоростью υ. На расстоянии l от напорного резервуара находится задвижка, которую можно закрыть как угодно быстро (рис. 9.1). Предположим, что закрытие произошло мгновенно. В результате остановки жидкости произойдет резкое повышение давления в трубе вследствие перехода кинетической энергии остановившихся слоев жидкости в потенциальную энергию сжатой жидкости. При этом в первую очередь давление увеличится непосредственно у задвижки после остановки первых слоев жидкости. Затем, по мере остановки последующих слоев, увеличение давления будет быстро распространяться вверх по трубопроводу, создавая волну повышенного давления. Повышение давления, распространяясь вверх по трубопроводу с большой скоростью, вызывает сжатие жидкости и растяжение стенок трубы. Указанная упругая деформация жидкости и трубы происходит со скоростью распространения повышения давления по длине трубы. Скорость распространения упругих деформаций называется скоростью распространения ударной волны.
Рис 9.1 После того, как остановится последний слой жидкости у резервуара, к которому подсоединен трубопровод, давление у задвижки достигает максимального значения, и вся жидкость в трубопроводе будет сжата. Но так как в этот момент давление в резервуаре будет меньше давления в трубопроводе, то жидкость придет в движение по направлению к резервуару. В результате произойдет резкое понижение давления в трубопроводе. Понижение давления, передающееся от слоя к слою и распространяющееся по направлению к задвижке, называется обратной ударной волной. Время пробега прямой (от задвижки к резервуару) и обратной ударной волн составляет длительность фазы гидравлического удара ТФ. Когда давление снизится во всем трубопроводе, жидкость остановится, находясь по пониженным давлением. Так как давление в резервуаре превышает давление в трубопроводе, то жидкость начинает обратное движение к задвижке с восстановлением скорости и давления, поэтому снова произойдет гидравлический удар. Он будет характеризоваться меньшим повышением давления, т.к. часть энергии потеряна. За этой обратной ударной волной последует другая, т.е. повторится фаза гидравлического удара и т.д.
На рис. 9.2 показана диаграмма изменения во времени давления у задвижки при гидравлическом ударе, из которой видно, что повышение давления (ударное давление) может во много раз превышать давление, имеющееся в условиях статического напора р0.
Рис 9.2
где ρ – плотность жидкости; d – диаметр трубопровода. В момент времени τ, соответствующий закрытию задвижки, количество движения равно:
За отрезок времени ∆τ повышение давления распространяется от задвижки до резервуара, жидкость в трубопроводе будет сжата и неподвижна (υ=0), поэтому
Определим сумму импульсов всех сил, действовавших на массу жидкости m в течение времени ∆τ. Импульс силы тяжести и силы давления со стороны стенок трубопровода равен нулю, т.к. эти силы нормальны оси трубопровода. Силы давления на торцевые сечения дают в сумме импульс, равный:
где ∆р – повышение давления у задвижки (ударное давление). Импульсами касательных напряжений на стенке можно пренебречь из-за их малости. Так как
Решаем уравнение (9.5) относительно ∆р и получаем
где С учетом формулы скорости распространения ударной волны, уравнение (9.6) имеет вид:
По полученной зависимости (9.7) можно определить ударное давление жидкости в трубопроводеи называется формулой Н.Е.Жуковского. Из зависимости (9.7) следует, что величина ударного давления зависит от рода жидкости, начальной скорости движения жидкости в трубопроводе и скорости распространения ударной волны. В свою очередь скорость с зависит от упругих свойств жидкости и материала стенок трубопровода. Если бы стенки трубопровода были абсолютно жесткими, то скорость распространения ударной волны совпадала бы со скоростью распространения звука в жидкости и ее можно определить по формуле
где Е0 – модуль упругости жидкости, Па. Для воды модуль упругости Е0=1,96 ∙109 Па и следовательно, после подстановки численных данных в формулу (9.8) для воды получим с*=1435 м/с. В действительности стенки трубопровода являются упругими, поэтому скорость распространения ударной волны определяется по формуле
где Е1 – кажущийся модуль упругости жидкости. Кажущийся модуль упругости Е1 можноопределить по следующей зависимости:
где d – диаметр трубопровода; Е – модуль упругости материала стенок трубопровода, например, для стали Е=1,96 ∙1011 Па; δ – толщина стенок трубопровода. Таким образом, в развернутом виде формула Н.Е.Жуковского (9.7) имеет вид:
Из формулы (9.11) следует, что чем выше эластичность материала (т.е. чем меньше модуль упругости материала стенок трубопровода) и чем больше диаметр трубопровода и меньше толщина стенок, тем меньше величина ударного давления. Формулы Жуковского справедливы при очень быстром закрытии крана или, точнее говоря, когда время закрытия:
где Тф – фаза гидравлического удара. При этом условии имеет место прямой гидравлический удар. Одним из средств уменьшения ударного давления является замедленное перекрытие трубопровода. При Если время полного закрытия задвижки τзак больше, чем длительность фазы гидравлического удара Тф, то повешение давления можно определить по формуле
Другой способ понижения ударного давления состоит в использовании специальных устройств – гасителей гидравлических ударов (клапаны, демпфирующие воздушные колпаки и др.). Следует иметь в виду, что гидравлический удар является не только вредным явлением. Колебательный характер изменения давления при гидравлическом ударе был использован при создании гидротаранов, предназначенных для перемещения жидкостей в системах водоснабжения сельских местностей.
Вопросы для самопроверки 1. Какое техническое явление называется гидравлическим ударом? Каков его механизм? 2. Что называется скоростью распространения ударной волны? По какой формуле она рассчитывается? 3. Что называется обратной ударной волной? Что представляет собой фаза гидравлического удара? 4. Запишите формулу Н.Е. Жуковского? Что из этой формулы следует? 5. Какие способы понижения ударного давления Вы знаете?
ГЛАВА 10 ГИДРОДИНАМИЧЕСКОЕ ПОДОБИЕ При изучении движения реальных жидкостей встречается много трудностей потому, что на характер движения и происходящие при этом процессы влияют многие факторы. Важным этапом этого изучения является отбор тех факторов, которые являются определяющими для изучаемого процесса. Следующий этап изучения – это установление зависимости интересующей величины от системы выбранных определяющих факторов. Этот этап может выполняться двумя путями: аналитическим, основанным на законах механики и физики, и экспериментальным. Первый путь применим лишь для ограниченного числа задач и при том обычно лишь для упрощенных моделей и явлений. Другой путь, экспериментальный, в принципе может учесть многие факторы, но он требует научно обоснованной постановки опытов, планирования эксперимента, ограничения его объема необходимым минимумом и систематизация результатов опытов. При этом должно быть обосновано моделирование явлений. Эти задачи позволяют решать так называемая теория гидродинамического подобия, т.е. подобия потоков несжимаемой жидкости. Подобными называются такие потоки жидкости, у которых каждая характеризующая их физическая величина находится для любых сходственных точек в одинаковом отношении. Понятие гидродинамического подобия включает подобие поверхностей, ограничивающих потоки (геометрическое подобие); пропорциональность скоростей в сходственных и подобие траекторий движения сходственных частиц жидкости (кинематическое подобие); пропорциональность сил, действующих на сходственные частицы жидкости и пропорциональность масс этих частиц (динамическое подобие). Отношения однородных физических величин, постоянных во всех сходственных точках подобных потоков, называются коэффициентами (масштабами) подобия. Соответственно принятым в Международной системе единиц основным физическим величинам (длина L, время Т и масса М) выделяют три основные коэффициента подобия: линейный масштаб (
Зависимость (10.1) дает обобщенный закон динамического подобия Ньютона. Закон можно представить в виде:
В свою очередь зависимость (10.2) можно записать в виде:
где Ne – число Ньютона, безразмерная величина. Согласно зависимости (10.3) следует, что число Ньютона, пропорциональное отношению действующих на подобные частицы сил к силам инерции этих частиц, имеет одинаковое значение в сходственных точках подобных потоков. Для рассматриваемого ниже установившегося движения однородных несжимаемых жидкостей необходимыми и достаточными условиями гидродинамического подобия являются: 1. геометрическое подобие граничных поверхностей, омываемых потоками (включая в некоторых случаях и подобие шероховатостей стенок); 2. подобие кинематических краевых условий (подобное распределение скоростей во входных и выходных сечениях рассматриваемых объектов – каналов, местных сопротивлений и т.д.; 3. одинаковые значения критериев динамического подобия – безразмерных величин, пропорциональных отношениям сил инерции частиц жидкости к действующим на них силам вязкостного трения (число Рейнольдса Re) и силам тяжести (число Фруда Fr).
Условием пропорциональности сил инерции и сил вязкостного трения является одинаковое значение числа Re для потоков в натуре и модели (рис. 10.1): Рис 10.1
где υ – характерная скорость (обычно средняя в сечении потока); L – характерный размер (обычно диаметр сечения потока); ν – кинематическая вязкость жидкости. Условие (10.4) приводит к соотношениям для коэффициентов подобия:
и для скоростей в натуре и модели:
Условием пропорциональности сил инерции и сил тяжести является одинаковое значение числа Fr для потоков в натуре и модели:
где g – ускорение свободного падения. Так как ускорение свободного падения g в натуре и модели практически всегда одинаково (масштаб ускорений kg=1), условие (10.7) приводит к соотношению для коэффициентов подобия:
и для скоростей в натуре и модели:
Подобие потоков в натуре и модели требует одновременного выполнения условий (10.4) и (10.7) для чисел Re и Fr или условий (10.5) и (10.8) для коэффициентов подобия. Последнее, возможно только тогда, когда масштабы линейных размеров и вязкостей находятся в следующем соотношении:
Из соотношения (10.10) следует, что для моделей, имеющих меньшие по сравнению с натурой размеры, должна применяться менее вязкая жидкость:
При выполнении условий подобия все безразмерные характеристики потока, т.е. безразмерные комбинации различных физических величин(например, коэффициенты сопротивления ξ, скорости φ, расхода μ и т.д.), имеют в натуре и модели одинаковое численное значение.
Вопросы для самопроверки 1. Какие потоки жидкости могут называться подобными? 2. Что подразумевает под собой геометрическое, кинематическое и динамическое подобие? 3. Что называется коэффициентами (масштабами) подобия? Сколько выделяется основных коэффициентов подобия? 4. За какие условия пропорциональности отвечают числа Рейнольдса и Фруда?
ЛИТЕРАТУРА
1. Башта.Т.М., Руднев С.С., Некрасов Б.Б. и др. Гидравлика, гидромашины и гидроприводы. – М.: Машиностроение, 1982, – 424с. 2. Богомолов А.И., Михайлов К.А. Гидравлика. – М.: Стройиздат, 1964, – 632 с. 3. Сборник задач по машиностроительной гидравлике. /Под редакцией И.И. Куколевского и Л.Г. Подвидза. – М.: Машиностроение, 1981, – 464 с.
© Оксана Николаевна Соколенко
Конспект лекций по курсу «Основы гидромеханики» для студентов дневной и заочной форм обучения направления 6.070104 «Морской и речной транспорт»
Тираж ____________ экз. Подписано к печати __________ Заказ № ___________ Объем _______ п.л. Изд–во «Керченский государственный морской технологический университет» 98309 г. Керчь, ул. Орджоникидзе, 82. Цена _______ грн.
|
||||||||||||
|
Последнее изменение этой страницы: 2017-01-26; просмотров: 523; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.212.145 (0.05 с.) |

 Установим расчетную зависимость ударного давления при мгновенном закрытии задвижки. С этой целью воспользуемся теоремой механики твердого тела: изменение количества движения тела за некоторый отрезок времени равно сумме импульсов сил, действовавших не него в течение того же отрезка времени. Целесообразность применения данного закона механики твердого тела обусловлена тем, что массу жидкости в трубопроводе при гидравлическом ударе можно считать постоянной, при чем масса жидкости равна:
Установим расчетную зависимость ударного давления при мгновенном закрытии задвижки. С этой целью воспользуемся теоремой механики твердого тела: изменение количества движения тела за некоторый отрезок времени равно сумме импульсов сил, действовавших не него в течение того же отрезка времени. Целесообразность применения данного закона механики твердого тела обусловлена тем, что массу жидкости в трубопроводе при гидравлическом ударе можно считать постоянной, при чем масса жидкости равна: , (9.1)
, (9.1) . (9.2)
. (9.2) . Приращение количества движения составляет
. Приращение количества движения составляет . (9.3)
. (9.3) , (9.4)
, (9.4) , то приравниваем правые части уравнений (9.3) и (9.4) и получаем
, то приравниваем правые части уравнений (9.3) и (9.4) и получаем . (9.5)
. (9.5) , (9.6)
, (9.6) – скорость распространения ударной волны.
– скорость распространения ударной волны. . (9.7)
. (9.7) , (9.8)
, (9.8) , (9.9)
, (9.9) , (9.10)
, (9.10) . (9.11)
. (9.11) , (9.12)
, (9.12) возникает непрямой гидравлический удар, при котором ударная волна, отразившись от резервуара, возвращается к крану (задвижке) раньше, чем он будет полностью закрыт. Очевидно, что повышение давления при этом будет меньше, чем при прямом ударе.
возникает непрямой гидравлический удар, при котором ударная волна, отразившись от резервуара, возвращается к крану (задвижке) раньше, чем он будет полностью закрыт. Очевидно, что повышение давления при этом будет меньше, чем при прямом ударе. . (9.13)
. (9.13) ), масштаб времени (
), масштаб времени ( ) и масштаб масс (
) и масштаб масс ( ). Масштабы всех остальных (произвольных) физических величин выражаются через основные в соответствии с формулами размерности этих величин. Так, масштабскоростей (
). Масштабы всех остальных (произвольных) физических величин выражаются через основные в соответствии с формулами размерности этих величин. Так, масштабскоростей ( ), масштаб сил одинаковой физической природы (
), масштаб сил одинаковой физической природы ( ), масштаб плотностей (
), масштаб плотностей ( ) и т.д. Используя выражения масштабов kυ и kρ, можно получить для масштаба сил следующую зависимость:
) и т.д. Используя выражения масштабов kυ и kρ, можно получить для масштаба сил следующую зависимость: . (10.1)
. (10.1) . (10.2)
. (10.2)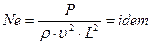 , (10.3)
, (10.3)
 , (10.4)
, (10.4) (10.5)
(10.5) . (10.6)
. (10.6) , (10.7)
, (10.7) (10.8)
(10.8) . (10.9)
. (10.9) . (10.10)
. (10.10) . (10.11)
. (10.11)


