
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Истечение жидкости через насадки
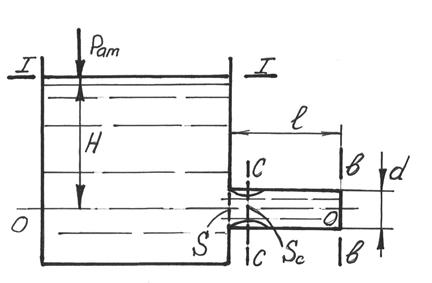
Решим задачу истечения жидкости через внешний цилиндрический насадок. Установим скорость вытекающей струи, расход жидкости и величину вакуума в сжатом сечении насадка. Рис 7.7 Предположим, что насадок имеет длину l и внутренний диаметр d (рис. 7.7). Для определения скорости вытекающей струи и расхода жидкости составим уравнение Д. Бернулли для двух сечений: 1-1 по свободной поверхности жидкости в резервуаре и В-В по выходному сечению насадка, относительно плоскости сравнения О-О, проходящей через ось насадка:
где Пренебрегаем слагаемым
где потери напора при протекании жидкости через насадок. Эти потери складываются из потерь напора на сужение струи до ее сжатого сечения (примерно те же, что и при истечении жидкости из отверстия с острой кромкой), потерь на расширение струи за сжатым сечением и на трение по длине насадка. Поэтому суммарный коэффициент сопротивления выражается так:
Опытные значения коэффициентов сопротивления для случая протекания жидкости через отверстия в тонкой стенке при отнесении к скорости в сжатом сечении лежат в пределах ξсуж=0,06-0.1. Коэффициент ξрасш находится через площади сжатого и несжатого сечений: Коэффициент сопротивления по длине определяется по обычной формуле Подставляя в уравнение (7.17) значение ∑ξ, получим
Решаем уравнение (7.19) относительно скорости вытекающей струи, получим
где Так как в выходном сечении В-В насадок работает полным сечением, то при определении расхода по выходному сечению коэффициент сжатия струи ε=1, а коэффициент расхода насадка составляет
Расход жидкости, вытекающей через насадок с учетом зависимостей (7.20) и (7.21), может быть выражен следующим образом:
Вышеуказанные зависимости справедливы для насадков всех типов, т.к. при их выводе не были сделаны какие-либо допущения относительно типа насадка. Из уравнений (7.20) и (7.21) видно, что при более коротких насадках коэффициент скорости φ, а следовательно, и коэффициент расхода μ будут увеличиваться, а при более длинных – уменьшаться. Опыт показывает, что минимальная длина насадка l, при которой после сжатия струи заполняется все сечение насадка и потери по длине становятся пренебрежимо малыми (ξдл=0), равна (3-4) d. Насадок такой длины будет обладать наибольшим коэффициентом расхода μ=φ=0,82.
Для определения величины вакуума в сжатом сечении насадка составим уравнение Д. Бернулли для двух сечений: сжатого сечения С-С и концевого В-В, относительно плоскости сравнения О-О, проходящей по оси насадка:
где потери энергии при расширении жидкости в насадке и потери энергии по длине при движении жидкости от сечения С-С до сечения В-В, Однако в виду того, что насадок имеет малую длину, потерями трения (по длине) можно пренебречь. Тогда
Так как вакуум – это недостаток давления до атмосферного, то очевидно, что
Согласно закона постоянства расхода жидкости
Выразим hвак через напор Н, приняв
Согласно уравнению (7.27), например, для внешнего цилиндрического насадка φ=0,82 и ε=0,64, имеем
Уравнение (7.28), подтверждаемое опытными данными, служит для определения величины вакуума и наибольшего напора, при котором вакуум еще не достигает своей предельной величины 10 м вод. ст. На практике предельное значение hвак не превышает 8 м вод. ст., т.к. при большем вакууме насадок работает неустойчиво. Воздух начинает подсасываться через выходное сечение насадка В-В и последний перестает работать полным сечением. Возможен полный или частичный отрыв струи жидкости от внутренней стенки насадка, с последующим уменьшением действующего напора, а следовательно, и пропускаемого напора. Понижению эффективности работы насадка, т.е. отрыву струи от его стенок, способствуют следующие условия:
1) малая длина насадка по сравнению с его диаметром (длина насадка приближается к минимальной длине, равной трем диаметрам, или становится меньше ее); 2) напор для насадка больше предельно допустимого (10 м вод. ст.), выше которого из-за большого вакуума в сжатом сечении происходит подсасывание воздуха через выходной конец насадка в зону сжатия струи. В первом случае вследствие недостаточной длины насадка струя жидкости не успевает расшириться и заполнить весь насадок; в него входит воздух и он начинает работать неполным поперечным сечением (происходит срыв вакуума). Во втором случае для предупреждения засасывания воздуха через конечное сечение насадка напор Н не должен превышать наибольшей величины, при которой создается предельно допустимое значение вакуума. Обозначим напор, соответствующий предельному вакууму, через Нпред. Тогда из уравнения (7.27) найдем
Вопросы для самопроверки 1. Какое отверстие называется отверстием в тонкой стенке? 2. Что такое сжатое сечение струи? Что называется коэффициентом сжатия струи? 3. Что называется насадком? Какие виды насадков Вы знаете? 4. Для чего применятся конический расходящийся насадок? Какие главные достоинства коноидального насадка? 5. Как рассчитать скорость истечения жидкости через незатопленное и затопленное отверстия в тонкой стенке? 6. Как рассчитать расход жидкости через незатопленное и затопленное отверстия в тонкой стенке? Коэффициент расхода жидкости? 7. Как определить время полного опорожнения резервуара при истечении при переменном напоре? 8. Как определить расход жидкости вытекающей через цилиндрический насадок? 9. Как определить допустимый (предельный) напор, при котором насадок будет работать полным сечением?
ГЛАВА 8
|
|||||||||
|
Последнее изменение этой страницы: 2017-01-26; просмотров: 604; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 13.58.82.79 (0.01 с.) |
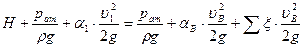 , (7.16)
, (7.16)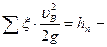 потери напора при протекании жидкости через насадок.
потери напора при протекании жидкости через насадок.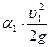 ввиду его малости, при этом полагаем, что кинетические коэффициенты Кориолиса α1 = αВ=1 и с учетом того, что полный напор равен Н, получаем уравнение (7.16) в виде:
ввиду его малости, при этом полагаем, что кинетические коэффициенты Кориолиса α1 = αВ=1 и с учетом того, что полный напор равен Н, получаем уравнение (7.16) в виде: , (7.17)
, (7.17) сумма всех коэффициентов сопротивления, характеризующих
сумма всех коэффициентов сопротивления, характеризующих . (7.18)
. (7.18)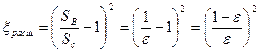 .
.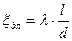 .
. . (7.19)
. (7.19)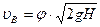 , (7.20)
, (7.20)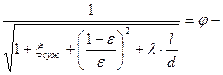 коэффициент скорости насадка.
коэффициент скорости насадка.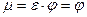 . (7.21)
. (7.21) . (7.22)
. (7.22) , (7.23)
, (7.23) суммарный коэффициент сопротивления, учитывающий
суммарный коэффициент сопротивления, учитывающий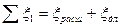 .
.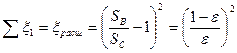 . (7.24)
. (7.24) . Поэтому, с учетом вышесказанного и полагая, что кинетические коэффициенты Кориолиса αс=αВ=1, получаем уравнение (7.23) в виде:
. Поэтому, с учетом вышесказанного и полагая, что кинетические коэффициенты Кориолиса αс=αВ=1, получаем уравнение (7.23) в виде: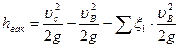 . (7.25)
. (7.25) и с учетом того, что
и с учетом того, что  , уравнение (7.25) примет вид:
, уравнение (7.25) примет вид: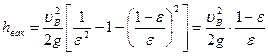 . (7.26)
. (7.26)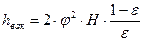 . (7.27)
. (7.27)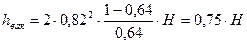 . (7.28)
. (7.28) . (7.29)
. (7.29)


