
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Теория ламинарного режима движения жидкости
ПРОФИЛЬ СКОРОСТИ В ЖИВОМ СЕЧЕНИИ КРУГЛОГО ТРУБОПРОВОДА
В круглом трубопроводе выберем поперечное сечение радиусом r и установим для него напряжение трения (рис. 5.1). Рис 5.1 С одной стороны, по закону внутреннего трения Ньютона имеем
Приравнивая правые части этих уравнений, имеем:
Интегрирование уравнения (5.1) дает
Постоянную интегрирования находим из условия: при r=r0 (на стенке) скорость υ=0. Тогда имеем
Следовательно, профиль скорости примет вид:
Зависимость (5.4) является уравнением параболы. Из уравнения (5.4) видно, что максимальное значение скорости имеет место при r=0 (на оси трубопровода):
Если уравнение (5.5) подставить в уравнение (5.4), то получим уравнение закона Стокса:
Для построения эпюры касательных напряжений снова обратимся к основному уравнению равномерного движения. Из него следует, что величина τ изменяется в зависимости от rГ по линейному закону, причем τ=τmax при r=r0, т.е. максимальные касательные напряжения будут на стенке трубопровода:
РАСХОД ЖИДКОСТИ Определим расход жидкости по трубопроводу, считая известным поле скоростей в живом сечении. Для этого выберем элементарное кольцевое сечение толщиной dr, имеющее радиус r (рис. 5.1). Элементарный расход равен:
Интегрирование уравнения (5.8) дает
или где d – диаметр трубопровода. Зависимость (5.10) называется уравнением Пуазейля. Определим среднюю скорость потока жидкости, пользуясь законом сплошности потока:
или т.е.
ПОТЕРИ НАПОРА ПО ДЛИНЕ КРУГЛОГО ТРУБОПРОВОДА Найдем потери напора по длине трубопровода, пользуясь зависимостью (5.12):
где l – длина трубопровода. Отсюда
Из уравнения (5.14) следует, что при ламинарном режиме движения потери по длине пропорциональны средней скорости в первой степени: hдл~ Преобразуем уравнение (5.14). Для этого домножим числитель и знаменатель правой части на 2∙υср. Получим
где Re – число Рейнольдса. Из уравнения (5.15) следует, что потери напора по длине выражаются через скоростной напор.
Величину, показывающую, во сколько раз напор, затраченный на преодоление трения, отличается от скоростного напора, называетсякоэффициентом сопротивления по длине:
Отношение
следовательно
Подставим зависимость (5.17) в уравнение (5.15) и получим уравнение для расчета потерь напора по длине при ламинарном режиме движения жидкости:
Полученное уравнение (5.19) называется формулой Дарси-Вейсбаха.
Вопросы для самопроверки 1. Какой профиль будет иметь эпюра скорости при ламинарном режиме движения жидкости? 2. В каком месте живого сечения круглого трубопровода будет наблюдаться максимальная скорость движения жидкости? Где будут наблюдаться максимальные касательные напряжения? 3. Чему будет равна средняя скорость движения жидкости при ламинарном режиме течения? 4. Как рассчитываются потери напора по длине при ламинарном режиме течения? 5. Запишите формулу Дарси – Вейсбаха? Что называется коэффициентом гидравлического трения? Чему он равен при ламинарном режиме течения?
ГЛАВА 6
|
||||||||
|
Последнее изменение этой страницы: 2017-01-26; просмотров: 214; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.116.40.177 (0.007 с.) |

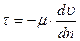 , а с другой стороны, по основному уравнению равномерного движения:
, а с другой стороны, по основному уравнению равномерного движения: , т.к.
, т.к. 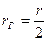 .
.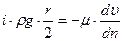 . Отсюда
. Отсюда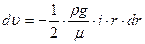 . (5.1)
. (5.1)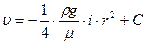 . (5.2)
. (5.2)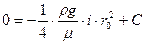 или
или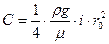 . (5.3)
. (5.3)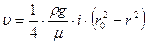 . (5.4)
. (5.4) . (5.5)
. (5.5)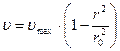 . (5.6)
. (5.6)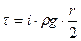 . (5.7)
. (5.7)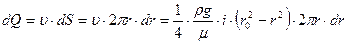 . (5.8)
. (5.8) , (5.9)
, (5.9) , (5.10)
, (5.10) , (5.11)
, (5.11)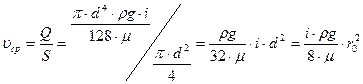 , (5.12)
, (5.12)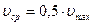 и тогда уравнение (5.4) можно записать в виде:
и тогда уравнение (5.4) можно записать в виде: . (5.13)
. (5.13)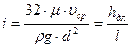 ,
, . (5.14)
. (5.14)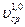 .
.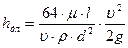 или
или  , (5.15)
, (5.15) . (5.16)
. (5.16) , входящее в зависимость (5.16), называется коэффициентом гидравлического трения(коэффициент Дарси):
, входящее в зависимость (5.16), называется коэффициентом гидравлического трения(коэффициент Дарси):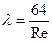 , (5.17)
, (5.17)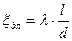 . (5.18)
. (5.18)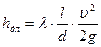 . (5.19)
. (5.19)


