
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Турбулентном режиме движения жидкости
В § 5.3 было показано, что расчет потерь напора по длине при ламинарном режиме движения жидкости производится по теоретической зависимости (5.19):
Приемлем ли такой метод для расчета потерь напора по длине при турбулентном режиме движения жидкости? В виду сложности структуры турбулентного потока, такой зависимости пока не получено. Тем не менее, экспериментальные данные показывают, что при турбулентном режиме движения, как и при ламинарном, потери напора по длине пропорциональны скоростному напору. Поэтому для турбулентного режима, как и для ламинарного, потери напора по длине могут быть рассчитаны по формуле Дарси-Вейсбаха (5.19). Однако, в отличие от ламинарного режима движения жидкости, нахождение коэффициента гидравлического трения λ для турбулентного потока невозможно теоретическим путем. В связи с этим были проведены экспериментальные исследования гидравлического сопротивления трубопроводов, на основании которых получены эмпирические зависимости для расчета коэффициента λ при турбулентном режиме движения. Приведем основные сведения, касающиеся данного вопроса. При турбулентном режиме движения жидкостей коэффициент гидравлического трения зависит не только от значения числа Re, но и от шероховатости стенок труб. Последняя причина может быть количественно оценена некоторой усредненной величиной абсолютной шероховатости ∆, представляющей собой среднюю высоту выступов неровностей на внутренней поверхности труб. Величина ∆ зависит от материала трубопровода, способа изготовления и срока его эксплуатации. Влияние шероховатости на коэффициент λ определяется соотношением между величиной ∆ и толщиной вязкого подслоя δ, движение жидкости в котором можно считать ламинарным.
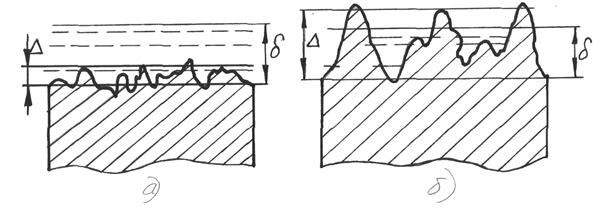
На рис. 6.3,а показан случай, когда δ > ∆, то такие трубы называются гидравлически гладкими. При δ < ∆ (рис. 6.3,б), трубы считаются гидравлически шероховатыми. Рис 6.3 Как было указано выше (§ 6.1), понятия «гладка» и «шероховатая» труба являются относительными. Это подтверждается опытными данными, показывающими, что при турбулентном режиме движения возможны три различные зоны трения (сопротивления): 1) зона гладкого сопротивления (зона гладких труб или зона Блазиуса) – величина λ зависит только от числа Re;
2) переходная зона от гладких к шероховатым трубам (зона доквадратичного сопротивления) – величина λ зависит как от числа Re, так и от относительной шероховатости ε; 3) зона гидравлическим шероховатых труб (зона квадратичного сопротивления или автомодельная) – величина λ зависит от шероховатости ε. Опыт также показывает, что при одной и той же абсолютной шероховатости ∆ ее влияние на величину гидравлических потерь в трубах разного диаметра различно. Следовательно, целесообразно ввести понятие относительной шероховатости (отношение величины абсолютной шероховатости трубопровода к его диаметру): Первые опыты для выявления характера зависимости λ от числа Re и ε были проведены в 1933 г. И. Никурадзе в гладких латунных трубах и трубах с искусственной равномерно-зернистой шероховатостью из кварцевого песка.
В последние годы были проведены исследования гидравлического сопротивления технических (реальных) трубопроводов. В результате получены зависимости, которые отличаются от тех, которые ранее получил И. Никурадзе. Данные зависимости представлены на графике ВТИ (Г.А. Мурина) (рис. 6.4). Рис 6.4
§ 6.3. МЕСТНЫЕ ПОТЕРИ НАПОРА ПРИ ТУРБУЛЕНТНОМ РЕЖИМЕ ДВИЖЕНИЯ ЖИДКОСТИ
Рассмотрим один из случаев местного сопротивления – внезапное расширение трубопровода. Наблюдения показывают, что поток, выходящий из узкой трубы, не сразу заполняет все поперечное сечение широкой трубы. В месте расширения жидкость отрывается от стенок и далее движется в виде свободной струи, отделенной от остальной жидкости поверхностью раздела
(рис. 6.5). Рис 6.5 Поверхность раздела неустойчива, на ней возникают вихри, в результате чего транзитная струя перемешивается с окружающей жидкостью. Струя постепенно расширяется, пока, наконец, на некотором расстоянии l от начала расширения не заполняет все поперечное сечение широкой трубы. В кольцевом пространстве между струей и стенками трубы жидкость находится в вихревом движении: циркулирует из струи к стенкам и обратно. Поэтому на участке трубопровода между сечениями 1-1 и 2-2 существуют значительные потери напора.
Опыты показывают, что в любом местном сопротивлении (краны, задвижки, повороты и пр.) потери напора пропорциональны скоростному напору и могут быть определены выражением:
где ξм.с. – коэффициент местного сопротивления. Если формулу (6.8) сравнить с формулой для определения потерь напора по длине, то можно заметить, что они сходственны по структуре. Для того, что формула (6.8) стала расчетной, необходимо знать величины ξм.с. для интересующих нас местных сопротивлений Установим ξм.с. для внезапного расширения. Пусть средняя скорость потока в сечениях 1-1 и 2-2 равны υ1 и υ2, давление р1 и р2, площади живого сечения – S1 и S2 соответственно (рис. 6.5). Находим потери напора между сечениями 1-1 и 2-2 по уравнению Бернулли для реальной жидкости, полагая в нем α1=α2=1:
Полученное уравнение (6.9) преобразуем, используя теорему импульсов: изменение количества движения жидкости между сечениями 1-1 и 2-2 при движении ее вдоль оси О-О равно импульсу суммы проекций всех сил, действующих на объем жидкости, на ту же ось. Записывая в левой части приращение количества движения, а в правой – импульс, получаем
где Q – расход жидкости; dτ – элементарный отрезок времени. Считая, что
Из уравнения (6.11) следует, что
Подставим выражение (6.12) в уравнение (6.9)
или
Выражение (6.14) называется формулой Борда. Для удобства проведения расчетов формулу (6.14) целесообразно преобразовать с учетом уравнения постоянства расхода (3.3):
Вынесем скоростной напор за скобку и получим
где Коэффициентывсех остальных видов местных сопротивленийявляются справочными величинами. Вопросы для самопроверки 1. Чему равна средняя скорость жидкости при турбулентном режиме движения? 2. Сколько условных зон различают в турбулентном потоке? Как они называются? 3. Как рассчитывается динамическая скорость? Как определить толщину пограничного слоя? 4. Что называется масштабом турбулентности? 5. Как рассчитываются потери по длине при турбулентном режиме движения? 6. Какие трубопроводы называются гидравлически гладкими, а какие гидравлически шероховатыми? 7. Что такое гидравлические зоны трения? Сколько различают таких зон? Что называется относительной шероховатостью трубопровода? 8. Запишите формулу для расчета потерь в местных сопротивлениях? Что называется коэффициентом местного сопротивления?
ГЛАВА 7
|
|||||||||||||||
|
Последнее изменение этой страницы: 2017-01-26; просмотров: 1240; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.22.119.251 (0.009 с.) |
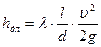 .
.
 .
.

 , (6.8)
, (6.8)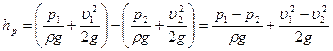 . (6.9)
. (6.9) , (6.10)
, (6.10) , разделим каждый член уравнения (6.10) на
, разделим каждый член уравнения (6.10) на  , получим
, получим . (6.11)
. (6.11) или
или  . (6.12)
. (6.12) (6.13)
(6.13)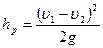 . (6.14)
. (6.14) . Тогда уравнение (6.14) имеет вид:
. Тогда уравнение (6.14) имеет вид: .
. или
или  , (6.15)
, (6.15) – коэффициент сопротивления внезапного расширения.
– коэффициент сопротивления внезапного расширения.


