Основное уравнение равномерного движения

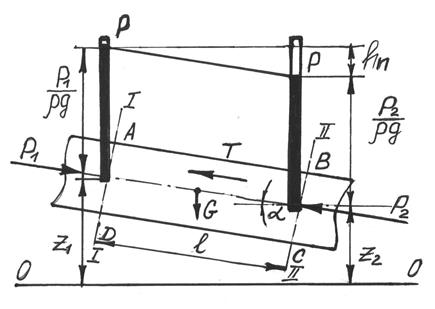
Предположим, что в канале с постоянным живым сечением S равномерно движется жидкость (рис. 4.3). Угол наклона потока к горизонту равен α, смоченный периметр составляет П.

Рис 4.3

Каково влияние площади живого сечения, смоченного периметра, длины канала, рода жидкости на потери напора при равномерном движении? На данный вопрос дает ответ основное уравнение равномерного движения.

Известно, что равномерное движение устанавливается при взаимном уравновешивании всех действующих в жидкости сил, поэтому сумма проекций внешних сил, приводящих жидкость в движение, на любую ось, должна быть равна сумме проекций сил сопротивления на ту же ось.

Проведем сечения 1-1 и 2-2 на расстоянии l друг от друга, выберем горизонтальную ось 0-0. Внешними силами, действующими на объем жидкости ABCD, являются силы давления Р₁ и Р₂, а также сила тяжести G. Найдем эти силы: ; ; , где р₁ и р₂ – давления соответственно в сечениях 1-1 и 2-2. Действию данных внешних сил оказывают сопротивление силы внутреннего трения в жидкости и силы трения жидкости о стенки канала. Суммарный эффект сил сопротивления можно определить в виде общей силы сопротивления , где τ – величина силы трения, приходящаяся на единицу внутренней поверхности объема ABCD.

Составим уравнение проекций внешних сил и сил сопротивления на ось 0-0:

.

С учетом, что , получаем

.

Разделим полученное уравнение на ρg∙S:

.

Сгруппируем слагаемые левой части:

. (4.2)

Т.к. средние скорости для сечений 1-1 и 2-2 одинаковы (υ₁=υ₂), то уравнение (4.2) можно записать в виде:

. (4.3)

В левой части уравнения (4.3) получена разность гидродинамических напоров для сечений 1-1 и 2-2, которая в соответствии с уравнением Бернулли равна потери напора h_пот. Тогда получаем

. (4.4)

Уравнение (4.4) называется основным уравнением равномерного движения. Из него следует, что при равномерном движении потери напора прямопропорциональны длине канала, смоченному периметру, касательным напряжениям на стенке и обратнопропорциональны удельному весу жидкости и площади живого сечения канала. Уравнение (4.4) справедливо как для напорного движения в трубопроводах, так и для безнапорного движения в открытых руслах.

Если в сечениях 1-1 и 2-2 установить пьезометры, то по высоте поднятия жидкости в них несложно определить величину h_{пот .} Проведя преобразования: ; , где i – гидравлический уклон (потери гидродинамического напора, приходящиеся на единицу длины), уравнение (4.4) примет вид:

. (4.5)

 

Вопросы для самопроверки

1. Какие режимы течения жидкости Вы знаете?

2. При каком режиме течения жидкости начинает наблюдаться поперечное перемещение частиц?

3. Запишите формулу числа Рейнольдса? Что характеризует число Рейнольдса?

4. При каком числе Рейнольдса происходит переход от ламинарного режима к турбулентному?

5. Запишите основное уравнение равномерного движения? Что из него следует?

 

ГЛАВА 5