
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Расходная характеристика имеет размерность расхода, и ее следует рассматривать как расход в трубе при гидравлическом уклоне, равном единице.
Преобразуем уравнение (8.2), с учетом формулы Павловского (
Учитываем, что В приложениях многих книг по гидравлике для стандартных диаметров труб приводятся значения расходных характеристик. Поскольку в литературе имеются готовые значения К для труб различного диаметра, то для упрощения гидравлических расчетов трубопроводов целесообразно преобразовать вторую водопроводную формулу (
Из зависимости (8.3) видно, что
Поэтому, с учетом уравнений (8.3), (8.5) и (8.6) следует, что
где а – коэффициент, зависящий от геометрических размеров трубопро- вода, (справочная величина). Следовательно, вторая водопроводная формула примет вид:
а расход жидкости через трубопровод определится по формуле
РАСЧЕТ ДЛИННЫХ ТРУБОПРОВОДОВ РАСЧЕТ ПРОСТОГО ДЛИННОГО ТРУБОПРОВОДА Технически возможны два случая работы такого трубопровода: работа под уровень и работа в атмосферу. Работа под уровень. Пусть полная длина трубопровода равна l, а диаметр – d (рис. 8.2).
Рис 8.2 Запишем уравнение Бернулли для сечении 1-1 и 2-2 (по свободной поверхности жидкости в резервуарах) относительно плоскости сравнения О-О, проходящей по оси трубопровода:
Если площади резервуаров велики, скорости υ1 и υ2 пренебрежимо малы, и ими можно пренебречь. Кроме того, очевидно, что р1=р2=рат. С учетом всего перечисленного уравнение (8.10) упростится, и будет иметь вид:
где Н – разность уровней в резервуарах.
Работа в атмосферу. Пусть трубопровод состоит из трех участков труб диаметрами d1, d2, d3 и длиной l1, l2, l3 (рис. 8.3).
Рис 8.3 Применим формулу (8.8) для каждого из участков трубопровода и получим систему уравнений для определения потерь напора по длине по трем участкам:
Соответственно общие потери напора будут равны сумме найденных потерь напора по длине по трем участкам:
Если обозначить через
где Р – величина проводимости трубопровода. По формуле (8.14) находят потери напора hдл при известном расходе Q. Если известны потери напора hдл, а требуется найти Q, то очевидноравенство:
|
||||||||
|
Последнее изменение этой страницы: 2017-01-26; просмотров: 538; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.137.192.3 (0.005 с.) |
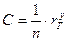 , где n – коэффициент шероховатости стенок трубопровода; y – переменный показатель степени, равный
, где n – коэффициент шероховатости стенок трубопровода; y – переменный показатель степени, равный 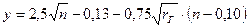 ):
): . (8.4)
. (8.4) , следовательно при неизменном коэффициенте шероховатости (n=const), расходная характеристика является функцией только диаметра трубы:
, следовательно при неизменном коэффициенте шероховатости (n=const), расходная характеристика является функцией только диаметра трубы:  .
. 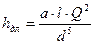 ) таким образом, чтобы расходная характеристика находилась в ней в явном виде. Отсюда, с учетом того, что
) таким образом, чтобы расходная характеристика находилась в ней в явном виде. Отсюда, с учетом того, что  , имеем
, имеем . (8.5)
. (8.5) . (8.6)
. (8.6)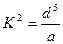 , (8.7)
, (8.7)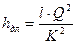 , (8.8)
, (8.8) . (8.9)
. (8.9)
 . (8.10)
. (8.10) , (8.11)
, (8.11) Следовательно, величина Н расходуется только на преодоление гидравлического сопротивления трубопровода.
Следовательно, величина Н расходуется только на преодоление гидравлического сопротивления трубопровода.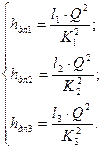 (8.12)
(8.12) или
или 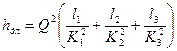 . (8.13)
. (8.13)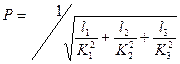 , то уравнение (8.13) будет иметь вид:
, то уравнение (8.13) будет иметь вид: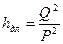 , (8.14)
, (8.14)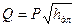 . (8.15)
. (8.15)


