
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Уравнение постоянства расхода
Рассмотрим трубопровод переменного сечения. Будем исходить из того, что движение жидкости в трубопроводе установившееся и не существует объединения и разъединения потоков. Тогда, для данного случая движения жидкости будет соблюдаться условие:
где ρ – плотность жидкости, кг/м3; υ – средняя скорость движения жидкости, м/с;
Тогда, для рис. 3.3 имеем
Рис 3.3 Выражение (3.2) называется уравнением постоянства расхода. Это уравнение показывает, что при установившемся движении, несмотря на изменение средних скоростей и площадей живых сечений по длине потока, расходы в нем одинаковы.
Для капельных жидкостей, при ρ=const, уравнением (3.2) имеет вид:
Из уравнения (3.3) следует, что средниескорости капельной жидкости обратно пропорциональны площадям соответствующих поперечных живых сечений.
ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ДВИЖЕНИЯ Л. ЭЙЛЕРА Выделим в движущейся жидкости элементарный параллелепипед, отбросив всю внешнюю область жидкости и заменив ее влияние на грани параллелепипеда силами гидростатического давления (рис. 3.4).
Рис 3.4 Если к действующим силам выделенного движущегося параллелепипеда: гидростатическим давлениям и собственному весу – добавить (с обратным знаком) силы инерции, то можно рассматривать движущийся параллелепипед, как находящийся в покое. Силы гидростатического давления должны быть направлены по нормалям внутрь параллелепипеда, и каждая из этих сил равна произведению гидростатического давления в центре тяжести его грани на площадь этой грани. Обозначая гидростатическое давление на некоторых гранях параллелепипеда (точки А, В, С) через р и учитывая непрерывность изменения давления в жидкости, т.е. функциональную зависимость давления от координат точек, найдем, что давления на противоположных гранях параллелепипеда отличаются от давлений в точках А, В, С соответственно на: Из объемных сил, действующих на параллелепипед, имеется только сила его собственного веса, относящаяся к массовым силам. Обозначим равнодействующую веса параллелепипеда через G; направление ее действия примем таким, как показано на рис. 3.4; в этом случае ее составляющие по координатным осям будут выражаться положительными величинами.
Собственный вес параллелепипеда определится как произведение его массы на ускорение силы тяжести
где dx, dy, dz – стороны параллелепипеда; ρ – постоянная плотность жидкости; g – ускорение массовой силы, в данном случае ускорение силы тяжести. Обозначим проекции ускорения на оси х, у и z соответственно через Х, Y и Z, получим следующие выражения для проекций силы G на координатные оси:
Силы инерции следует определять тоже в виде произведений массы параллелепипеда на ускорение по соответствующим координатным осям. Если обозначить через υ полную скорость движения жидкости, а тем самым и параллелепипеда, а через υх, υу, υz составляющие ее по координатным осям, то компоненты ускорения по координатным осям могут быть выражены так:
Полные составляющие сил инерции по координатным осям будут равны: После приложения сил инерции с обратным знаком, параллелепипед должен находиться в равновесии; поэтому сумма проекций на каждую ось x, y и z всех сил, действующих на рассматриваемый параллелепипед (сил гидростатического давления, равнодействующих массовой силы и силы инерции), должны быть равны нулю. Эти суммы могут быть представлены следующими выражениями:
Впервые эти дифференциальные уравнения были выведены Л. Эйлером (1755 г.), поэтому им присвоено наименование уравнений движения жидкости Л. Эйлера.
|
||||||||
|
Последнее изменение этой страницы: 2017-01-26; просмотров: 741; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.118.150.80 (0.006 с.) |
 ,
, S – площадь сечения трубопровода, м2.
S – площадь сечения трубопровода, м2.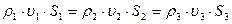 .(3.2)
.(3.2) . (3.3)
. (3.3)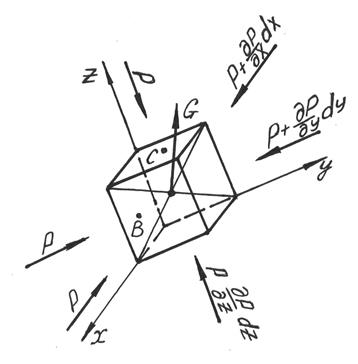
 ;
;  ;
;  .
.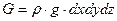 , (3.4)
, (3.4) (3.5)
(3.5)



 (3.6) Раскрывая скобки и деля каждое из уравнений на массу параллелепипеда
(3.6) Раскрывая скобки и деля каждое из уравнений на массу параллелепипеда  , т.е. приводя каждый член уравнения к единице массы жидкости, получим следующую систему уравнений:
, т.е. приводя каждый член уравнения к единице массы жидкости, получим следующую систему уравнений: (3.7)
(3.7)


