
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Расчет коротких трубопроводовСодержание книги
Поиск на нашем сайте
Рассмотрим работу короткого трубопровода, считая, что из резервуара жидкость вытекает в атмосферу. Пусть диаметр трубопровода d – постоянный по длине трубопровода l, суммарный коэффициент местных сопротивлений равен  (рис. 8.7). (рис. 8.7).
Рис 8.7 Запишем уравнение Бернулли для сечений 1-1 (по поверхности жидкости в резервуаре) и 2-2 (на выходе из трубопровода) относительно плоскости сравнения О-О, проходящей по оси трубопровода:
Для квадратичной зоны сопротивления имеем, что α1=α2=1. Отношением
Опуская индекс «2» из уравнения (8.22) найдем скорость движения жидкости по короткому трубопроводу:
где вода. Если живое сечение трубопровода обозначить через S, то расход жидкости через него определим как
Зависимости (8.23) и (8.24) являются основными при расчете коротких трубопроводов. Обычно возникают четыре основные задачи расчета коротких трубопроводов. Задача 1. Известен расход жидкости Q, длина трубопровода l и его диаметр d. Требуется определить потери напора hпот. В данной задаче сначала находим среднюю скорость движения жидкости ( Вышеизложенную последовательность расчета можно записать в виде схемы, следующим образом:
Задача 2. Жидкость движется по трубопроводу длиной l и диаметром d под действием напора Н. Требуется определить расход жидкости Q. Расчет производим методом последовательных приближений. Считаем, что трубопровод работает в квадратичной зоне сопротивления (напомним, что в этой зоне λ не зависит от Re, а следовательно, и расхода жидкости и определяется только величиной ε). Выбираем материал труб и срок их эксплуатации, по ним находим относительную шероховатость ε и определяем расчетным путем или по графику ВТИ, коэффициент гидравлического трения λ1. Затем находим коэффициент расхода ( Методика решения данной задачи схематично выглядит следующим образом:
Задача 3. При движении жидкости по трубопроводу длиной l под действием напора Н, необходимый расход жидкости Q. Требуется определить диаметр трубопровода d, обеспечивающий указанный необходимый расход жидкости. Непосредственное решение уравнения расхода относительно диаметра трубопровода невозможно, т.к. величина d входит одновременно в величины μ и S. Поэтому уравнение расхода решаем относительно произведения
Затем задаемся произвольным значением диаметра трубы d1 и находим скорость движения жидкости ( С целью уменьшения трудоемкости решения данной задачи целесообразно воспользоваться расчетно-графическим методом нахождения искомой величины диаметра трубопровода. Для этого, задавшись 3 – 4 значениями диаметра и определив соответствующие им произведения Последовательность решения задачи схематично выглядит следующим образом:
Задача 4. В трубопроводе длиной l, расход жидкости равен Q. Требуется определить диаметр трубопровода d и потери напора hпот. Сначала находим диаметр трубопровода. Для этого принимаем среднюю скорость движения жидкости в пределах (0,5 – 1,8 м/с). Для невязких жидкостей скорость можно устанавливать до 3 м/с. Затем находим диаметр из уравнения сплошности потока (
Вопросы для самопроверки 1. На какие группы делятся трубопроводы в зависимости от гидравлической схемы работы? 2. Какие основные задачи гидравлического расчета трубопроводов? 3. Запишите формулу расходной характеристики трубопровода? 4. Каковы основные задачи расчета простого длинного трубопровода? 5. Что представляет собой графо – аналитический метод расчета сложного длинного трубопровода? 6. Что называется характеристикой трубопровода и суммарной характеристикой трубопровода в целом? 7. Перечислите задачи, которые решаются при расчете коротких трубопроводов?
ГЛАВА 9
|
|||||||
|
Последнее изменение этой страницы: 2017-01-26; просмотров: 397; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.33 (0.008 с.) |


 . (8.21)
. (8.21) пренебрегаем вследствие ее малости и приняв во внимание, что р1=р2=рат, получаем уравнение (8.21) в виде:
пренебрегаем вследствие ее малости и приняв во внимание, что р1=р2=рат, получаем уравнение (8.21) в виде: . (8.22)
. (8.22) или
или  , (8.23)
, (8.23) – коэффициент расхода жидкости для трубопро-
– коэффициент расхода жидкости для трубопро- . (8.24)
. (8.24)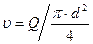 ), затем определяем режим движения жидкости, предварительно рассчитав число Рейнольдса (
), затем определяем режим движения жидкости, предварительно рассчитав число Рейнольдса ( ). Далее задаемся материалом труб и сроком их эксплуатации и находим из таблиц справочной литературы относительную шероховатость ε. После этого рассчитываем коэффициент гидравлического трения λ по зависимости, соответствующей найденному режиму движения и зоне гидравлического сопротивления или находим его по графику ВТИ. И наконец, находим, потери напора (
). Далее задаемся материалом труб и сроком их эксплуатации и находим из таблиц справочной литературы относительную шероховатость ε. После этого рассчитываем коэффициент гидравлического трения λ по зависимости, соответствующей найденному режиму движения и зоне гидравлического сопротивления или находим его по графику ВТИ. И наконец, находим, потери напора ( ).
). .
. ) и расход по формуле:
) и расход по формуле:  , где
, где  . Далее, по величине Q1 находим скорость движения жидкости
. Далее, по величине Q1 находим скорость движения жидкости  , а затем число Рейнольдса
, а затем число Рейнольдса  . По значению Re1 и ранее принятой величине относительной шероховатости ε находим вышеуказанным способом новое значение коэффициента гидравлического трения λ2. Затем рассчитываем уточненное значение коэффициента расхода (
. По значению Re1 и ранее принятой величине относительной шероховатости ε находим вышеуказанным способом новое значение коэффициента гидравлического трения λ2. Затем рассчитываем уточненное значение коэффициента расхода ( ) и уточненную величину расхода (
) и уточненную величину расхода ( ). Если значение расхода Q2 отличается от значения Q1 более чем на 5%, то величину Q1 отбрасываем, как неправильную и уточняем расход Q2 в такой же последовательности. Расчет производят до совпадения сравниваемых значений расхода с точностью не менее 5%.
). Если значение расхода Q2 отличается от значения Q1 более чем на 5%, то величину Q1 отбрасываем, как неправильную и уточняем расход Q2 в такой же последовательности. Расчет производят до совпадения сравниваемых значений расхода с точностью не менее 5%.
 методом последовательных приближений в следующем порядке. По заданным в условии величинам Q и H находим искомое произведение по формуле
методом последовательных приближений в следующем порядке. По заданным в условии величинам Q и H находим искомое произведение по формуле . (8.25)
. (8.25) ) и число Рейнольдса (
) и число Рейнольдса ( , где
, где  ). После этого выбираем материал труб и срок их эксплуатации, по таблицам и справочной литературе находим значение относительной шероховатости ε. Далее по известным величинам Rе1 и ε определяем коэффициент гидравлического трения λ1, а затем – коэффициент расхода (
). После этого выбираем материал труб и срок их эксплуатации, по таблицам и справочной литературе находим значение относительной шероховатости ε. Далее по известным величинам Rе1 и ε определяем коэффициент гидравлического трения λ1, а затем – коэффициент расхода ( ). Наконец, рассчитываем произведение
). Наконец, рассчитываем произведение  и сравниваем полученное значение с величиной, полученной по формуле (8.25). Если совпадения значений
и сравниваем полученное значение с величиной, полученной по формуле (8.25). Если совпадения значений 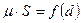 . Из данного графика по значению произведения
. Из данного графика по значению произведения 
 ). Полученное значение диаметра округляем до ближайшего стандартного значения, после чего уточняем величину скорости по уравнению сплошности потока (
). Полученное значение диаметра округляем до ближайшего стандартного значения, после чего уточняем величину скорости по уравнению сплошности потока ( , где d – округленное значение диаметра трубопровода). Далее определение потерь напора hпот совпадает с первой задачей расчета коротких трубопроводов, рассмотренной выше.
, где d – округленное значение диаметра трубопровода). Далее определение потерь напора hпот совпадает с первой задачей расчета коротких трубопроводов, рассмотренной выше.


