
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Сила давления жидкости на криволинейные
ПОВЕРХНОСТИ
Принцип решения данной задачи состоит в определении составляющих силы полного гидростатического давления по нескольким направлениям с последующим геометрическим сложением этих частных сил. Рис 2.12 Выделим на некоторой цилиндрической поверхности АВ (рис.2.12) элементарную площадку величиной dS. Ее центр тяжести погружен в жидкость на глубину h. Если внешнее давление на поверхности жидкости равно р0, то полное гидростатическое давление в центре тяжести площадки составит:
Произведения
Используя зависимости (2.45), систему уравнений (2.44) можно переписать в следующем виде:
После интегрирования системы уравнений (2.46) по площади поверхности АВ, имеем
Первые слагаемые в правой части системы уравнений (2.47) равны соответственно площадям проекций цилиндрической поверхности АВ на горизонтальную ХОУ и вертикальную YOZ плоскости, т.е.
Следовательно, вертикальная составляющая силы полного гидростатического давления равна сумме силы внешнего давления на горизонтальную проекцию цилиндрической поверхности АВ и веса жидкости в объеме АВСD, ограниченного цилиндрической поверхностью АВ, вертикальными плоскостями AD и ВС и свободной поверхностью жидкости. Интеграл
где hc – глубина погружения центра тяжести площадки Sz,y.
Тогда второе уравнение системы (2.47) имеет вид:
Уравнение (2.50) идентично уравнению (2.25). Следовательно, горизонтальная составляющая силы полного гидростатического давления, воздействующая на цилиндрическую поверхность АВ, равна силе абсолютного гидростатического давления, под воздействием которого находится вертикальная плоская стенка, равная по площади вертикальной проекции цилиндрической поверхности АВ. Складываем силы давления РГ и РВ по правилу параллелограмма, получаем силу полного гидростатического давления Р, действующего на цилиндрическую поверхность АВ:
Давление на поверхности жидкости чаще всего равно атмосферному, поэтому и для цилиндрических поверхностей нередко определяют воздействие лишь сил манометрического давления, т.е. давления самой жидкости. Вертикальные и горизонтальные составляющие сил избыточного (манометрического) давления находят также по уравнениям (2.48) и (2.50), в которых р0 принимают равным нулю:
ЗАКОН АРХИМЕДА
Закон Архимеда, открытый им за 250 лет до н.э., характеризует плавучесть тела, погруженного в жидкость. Для теоретического вывода закона Архимеда рассмотрим давление жидкости на тело, погруженное в нее. Допустим, что в жидкость погружено тело сферической формы. Выберем координатные оси так, как показано на рис. 2.13. Рис 2.13 Покажем силы, действующие на тело со стороны жидкости. Очевидно, что силы Р'x и P"x, а также P'y и P"y равны по величине и противоположны по направлению. Поэтому они исключаются из дальнейшего анализа. Проведем контурные линии АА' и ВВ", а также разделим тело на две части плоскостью АВ. На верхнюю часть поверхности, жидкость воздействует с силой P'z, а на нижнюю – P"z. Результирующая сила равна:
Отсюда,
Формула (2.54) выражает закон Архимеда, согласно которому сила, с которой жидкость воздействует на погруженное в нее тело, равно весу жидкости в объеме погруженного тела.
|
|||||||||||
|
Последнее изменение этой страницы: 2017-01-26; просмотров: 213; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.133.12.172 (0.011 с.) |
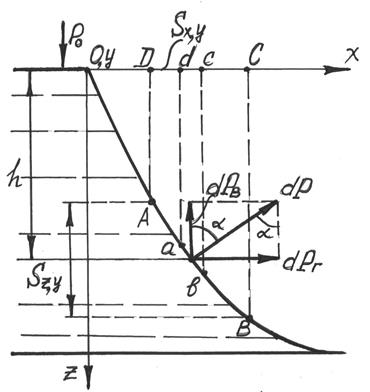
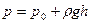 . Тогда элементарная сила полного гидростатического давления равна:
. Тогда элементарная сила полного гидростатического давления равна: 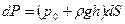 . Эта сила направлена по нормали к площадке dS, проведенной через центр ее тяжести. Разложим эту силу dP на вертикальную dPВ и горизонтальную dPГ составляющие:
. Эта сила направлена по нормали к площадке dS, проведенной через центр ее тяжести. Разложим эту силу dP на вертикальную dPВ и горизонтальную dPГ составляющие: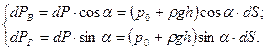 (2.44)
(2.44) и
и 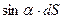 соответственно равны площадям проекций элементарной площадки dS на горизонтальную ХОУ и вертикальную YOZ плоскости, т.е.
соответственно равны площадям проекций элементарной площадки dS на горизонтальную ХОУ и вертикальную YOZ плоскости, т.е.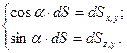 (2.45)
(2.45)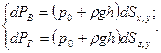 (2.46)
(2.46)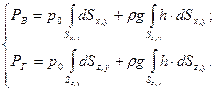 (2.47)
(2.47)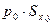 и
и 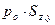 . Для нахождения интеграла
. Для нахождения интеграла 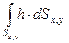 проведем через различные точки периметра площадки dS вертикальные образующие до пересечения с плоскостью XOY. В результате получим элементарный объем abcd, равный
проведем через различные точки периметра площадки dS вертикальные образующие до пересечения с плоскостью XOY. В результате получим элементарный объем abcd, равный 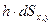 . Сравнивая это выражение с подынтегральным выражением, получаем, что величина интеграла равна объему фигуры ABCD. Тогда уравнение для определения вертикальной составляющей силы полного гидростатического давления перепишется в виде:
. Сравнивая это выражение с подынтегральным выражением, получаем, что величина интеграла равна объему фигуры ABCD. Тогда уравнение для определения вертикальной составляющей силы полного гидростатического давления перепишется в виде: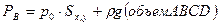 . (2.48)
. (2.48)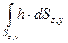 во втором уравнении системы (2.47) равен статическому моменту площади проекции цилиндрической поверхности АВ на вертикальную плоскость ZOY относительно оси OY:
во втором уравнении системы (2.47) равен статическому моменту площади проекции цилиндрической поверхности АВ на вертикальную плоскость ZOY относительно оси OY: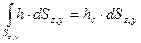 , (2.49)
, (2.49)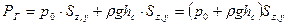 . (2.50)
. (2.50)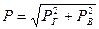 . (2.51)
. (2.51)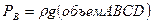 ; (2.52)
; (2.52)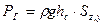 . (2.53)
. (2.53)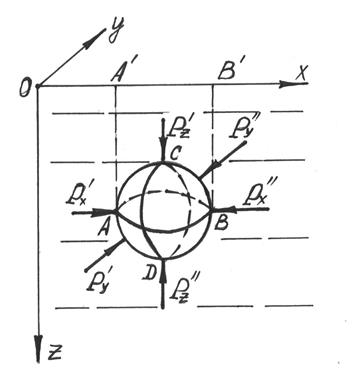
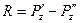 . Найдем силы P'z и P"z, воспользовавшись уравнением (2.52):
. Найдем силы P'z и P"z, воспользовавшись уравнением (2.52):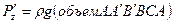 ;
; 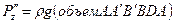 .
.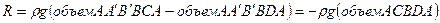 или
или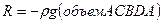 . (2.54)
. (2.54)


