
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Пьезометрическая высота. Вакуум
Превышение давления над атмосферным называетсяманометрическимилиизбыточным давлением:
где рм, р, ра – соответственно манометрическое, полное и атмосферное давления, Па. Если сосуд открыт в атмосферу, то давление на свободную поверхность жидкости равно атмосферному давлению: ро= ра. В этом случае манометрическое давление определится как
Размерность полного и манометрического давлений в системе МКГСС выражается как кГ/см2, в системе СИ – Н/м2 или Па. Давление можно измерять также высотой какой – либо жидкости (воды, ртути), выражая эту высоту в м или мм.
Если в точке А к резервуару, наполненному жидкостью, присоединить открытую в атмосферу трубку (рис.2.6), то в такой трубке жидкость поднимется на некоторую высоту h, большую или меньшую глубины воды в резервуаре в зависимости от того, будет ли ро больше или меньше ра. Рис. 2.6 Такие трубки называются пьезометрами или в общем случае манометрами. Высоту h называют пьезометрической или манометрической высотой. Пьезометрическая высота характеризует давление или, точнее говоря, измеряет его в линейных единицах. Одна техническая атмосфера равна давлению 1кГ/см2, или 10000 кГ/м2 (в системе МКГСС) и 98100 Н/м2 (в системе СИ); это отвечает следующей пьезометрической высоте h (высоте водяного столба):
Следовательно, одна техническая атмосфера измеряется высотой столба воды в 10 м (или ртути в 760 мм). Поэтому, пользуясь пьезометром или манометром, можно определить давление в любой точке жидкости путем отсчета высоты столба жидкости. Для пьезометров (жидкостных манометров) применяются стеклянные трубки диаметром не менее 10 мм в целях избежания явлений капиллярного поднятия. Для более точных отсчетов при малых давлениях пьезометры устанавливаются наклонно.
Если полное гидростатическое давление в какой – либо точке жидкости (рис.2.7) меньше атмосферного давления (р<ра), то манометрическое давление будет отрицательным. Знак минус указывает, что давление в рассматриваемом баллоне А меньше атмосферного. Рис 2.7 Отрицательное манометрическое давление, точнее, превышение атмосферного давления над полным называют вакуумом (от латинского vacuum – разряжение). Высоту столба жидкости, измеряющую вакуум, называют вакуумметрической и обозначают
Вакуум может меняться в пределах от 10 м вод. ст до нуля. Приборы для измерения вакуума называются вакуумметрами или обратными пьезометрами.
СИЛА ГИДРОСТАТИЧЕСКОГО ДАВЛЕНИЯ НА ПЛОСКУЮ ФИГУРУ
В этом параграфе будут рассмотрены два вопроса. 1. Как рассчитать силу полного и избыточного гидростатического давления на плоскую фигуру? 2. Где располагается центр давления (координаты точки приложения равнодействующей силы давления)?
Рис 2.8 Слева на нее действует гидростатическое давление. Фигура АВ расположена перпендикулярно плоскости чертежа и наклонена к горизонту под углом α. Выберем систему координат, как на рисунке. Мысленно вращая вокруг оси ОУ фигуру АВ, совместим ее с плоскостью чертежа. Выделим на фигуре бесконечно малую полоску площадью dS и высотой dy, погруженную на глубину h и отстоящую от оси ОХ на расстоянии y. Для нее полное гидростатическое давление равно:
а элементарная сила давления составит
Из Δ ОМN следует, что
Интегрируя данное выражение по всей площади фигуры S, получаем
Интеграл
где ус – расстояние от оси ОХ до центра тяжести площади фигуры АВ. Из Δ ОМсNc устанавливаем, что
и уравнение (2.23) в этом случае перепишется так:
или При этом сила избыточного гидростатического давления составляет
Следовательно, сила полного гидростатического давления на плоскую фигуру выражается произведением площади фигуры на величину полного гидростатического давления в ее центре тяжести, а сила избыточного гидростатического давления равна произведению площади фигуры на величину избыточного гидростатического давления в ее центре тяжести.
Теперь определим положение центра давления. Из механики твердого тела известно, что момент равнодействующей силы относительно выбранной оси равен сумме моментов, составляющих равнодействующую относительно той же оси. В нашем случае равнодействующей силой является сила избыточного гидростатического давления Составим выражение элементарного момента силы dP относительно оси ОХ:
После интегрирования уравнения элементарного момента силы dP по всей площади фигуры S, получаем
где Мс – суммарный момент элементарных сил;
Находим момент равнодействующей силы Р относительно оси ОХ:
где Мр – момент равнодействующей силы Р относительно оси ОХ; уd – координата искомого центра давления (плечо равнодействующей силы гидростатического давления Р). Так как Мс = Мр, то с учетом уравнений (2.27) и (2.28) получаем
или Введем в уравнение (2.29) вместо момента инерции Iх центральный момент инерции I0, т.е. момент инерции фигуры относительно оси, проходящей через центр ее тяжести. Величины Ix и I0 взаимосвязаны уравнением
Из уравнения (2.30) видно, что сила избыточного гидростатического давления приложена ниже центра тяжести фигуры на величину
|
||||||||||||
|
Последнее изменение этой страницы: 2017-01-26; просмотров: 1052; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.118.7.85 (0.011 с.) |
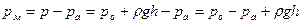 , (2.18)
, (2.18) . (2.19)
. (2.19)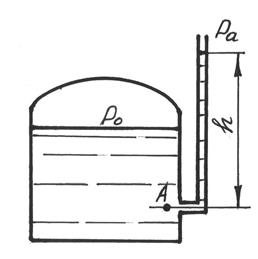
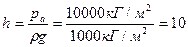 м вод. ст.
м вод. ст.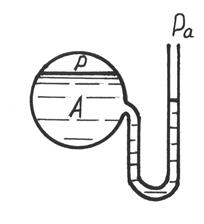
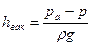 . (2.20)
. (2.20) В начале определим силу полного и избыточного гидростатического давления. Для получения расчетных формул воспользуемся основным уравнением гидростатики. Выберем плоскую фигуру АВ, как показано на рисунке 2.8.
В начале определим силу полного и избыточного гидростатического давления. Для получения расчетных формул воспользуемся основным уравнением гидростатики. Выберем плоскую фигуру АВ, как показано на рисунке 2.8.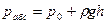 ,
,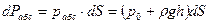 . (2.21)
. (2.21)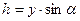 . Произведя эту замену в уравнении (2.21), имеем
. Произведя эту замену в уравнении (2.21), имеем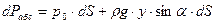 . (2.22)
. (2.22)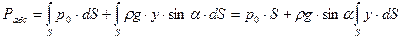 . (2.23)
. (2.23)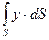 в выражении (2.23), есть статический момент площади фигуры АВ относительно оси ОХ, который равен:
в выражении (2.23), есть статический момент площади фигуры АВ относительно оси ОХ, который равен: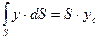 , (2.24)
, (2.24)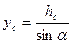 . Тогда, подставляя выражение, ус в уравнение (2.24) получаем
. Тогда, подставляя выражение, ус в уравнение (2.24) получаем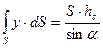 ,
,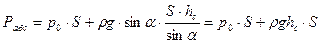 ,
,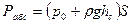 . (2.25)
. (2.25)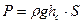 . (2.26)
. (2.26)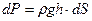 на площадки величиной dS.
на площадки величиной dS.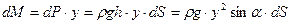 .
.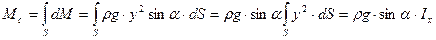 , (2.27)
, (2.27)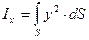 – момент инерции фигуры относительно оси ОХ.
– момент инерции фигуры относительно оси ОХ.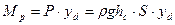 , (2.28)
, (2.28)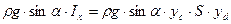
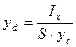 . (2.29)
. (2.29)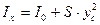 , поэтому окончательно имеем
, поэтому окончательно имеем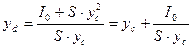 . (2.30)
. (2.30) , называемую эксцентриситетом.
, называемую эксцентриситетом.


