
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Типовые статистические алгоритмы вынесения заключения о профессиональной пригодности по результатам психологического и психофизиологического обследованияСодержание книги
Поиск на нашем сайте
При решении прикладных задач прогнозирования профессиональной пригодности специалистов для получения приемлемого по степени точности прогноза успешности профессиональной деятельности часто бывает недостаточно использования только одного теста. Повышение точности прогноза достигается путем использования набора разнообразных тестов, каждый из которых в отдельности связан с успешностью деятельности, т. е. обладает определенной прогностической валидностью. Для решения конкретной задачи не имеет смысла увеличивать количество тестов, направленных на оценку одного и того же свойства из перечня профессионально важных качеств. Тестовые результаты в этом случае высоко коррелируют между собой, и точность прогноза практически не возрастает. Точность прогноза возрастает в том случае, если тесты оценивают различные свойства индивида, влияющие на результаты его деятельности. Интегральная оценка по результатам тестирования должна учитывать степень связи тестовых показателей с успешностью деятельности и выраженность корреляции тестов между собой. Практически это достигается введением весовых коэффициентов для каждого тестового показателя, рассчитываемых таким образом, чтобы суммарная оценка была наиболее тесно связана с внешним критерием, т. е. наиболее точно предсказывала профессиональную успешность. Математический аппарат, наиболее часто используемый для этой цели, — множественный регрессионный анализ. Параметры уравнения множественной линейной регрессии рассчитываются по формуле (8.32):
где уа — значения прогнозируемой оценки профессиональной успешности; х, хТ...xmf — значения тестовых показателей; bv bv...bm — коэффициенты уравнения регрессии; а — смещение (свободный член уравнения регрессии). Решение уравнения состоит в определении его параметров, для чего необходимо предварительно рассчитать следующие статистические характеристики: средние арифметические значения психодиагностических показателей у, х\, х2,... Зся; средние квадратические отклонения ст, ал, ах2,... <Ухт; коэффициенты корреляций всех переменных между собой
Параметры уравнения прогноза рассчитываются путем решения системы т уравнений с т неизвестными:
Коэффициенты р чаще являются значениями регрессии для тех случаев, когда тестовые оценки внешнего критерия выражены в одной стандартной шкале. Если используются разные шкалы оценок, то P-коэффициенты следует преобразовать по формулам (8.34):
Свободный член уравнения регрессии рассчитывается по формуле (8.35)
Статистические характеристики качества уравнения множественной линейной регрессии рассчитываются по формулам (8.36)- (8.38): - коэффициент множественной детерминации (D)
- коэффициент множественной корреляции (R)
- стандартная ошибка уравнения прогноза (с л), определяющая среднее квадратическое отклонение истинных значений^ от значений прогнозируемой оценки, вычисленных по уравнению регрессии:
Величина стандартной ошибки уравнения прогноза указывает максимальное отклонение вычисленного значения от истинного значения прогнозируемой оценки у 68,3% (+- а) испытуемых. Значимость коэффициента множественной корреляции оценивается по критерию Фишера. При этом число степеней свободы зависит от количества наблюдений (л) и количества показателей (т). Следует сказать, что приведенный алгоритм расчета параметров уравнения множественной регрессии заложен в большинстве современных компьютерных статистических программ. От пользователя таких программ требуется лишь понимание того, что он хочет получить от компьютера, и корректный ввод данных. Другой, наиболее часто используемый в настоящее время в процедурах ППО методический подход, получил название нормативного. Его иллюстрацией в самом общем виде может служить метод многомерного шкалирования. Для каждого вида деятельности разрабатываются профессиографические характеристики с перечнем наиболее необходимых ПВК. Устанавливаются «минимальные пороги», достаточные для достижения заданной нормативами успешности деятельности. Реальные психофизиологическиехарактеристики обследуемого кандидата сравниваются с заданными. В зависимости от степени их соответствия выносится заключение о профессиональной пригодности. Например, для оценки кандидатов при отборе на военную службу по контракту разработаны оценочные таблицы (табл. 8.8) по принятым методикам. Пересечение показателей разных методик в таблице дает интегральную оценку профессиональной пригодности. Другой практический пример применения метода многомерного шкалирования в профессиональной психодиагностике — вынесение итогового заключения о профессиональной пригодности к поступлению в военное образовательное учреждение высшего профессионального образования (табл. 8.9). Созданные на основе многомерного шкалирования методические и организационные модели профессионального консультирования и профотбора в целом показали достаточно большую' эффективность (до 76-80% совпадения прогноза с реально показанной успешностью деятельности). Но следует сказать, что такая эффективность достигается кропотливой предварительной работой по апробированию, стандартизации и валидизации методик обследования, расчету надежности и достоверности получаемых психофизиологических показателей.
|
||||
|
Последнее изменение этой страницы: 2017-01-26; просмотров: 235; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 13.59.36.4 (0.006 с.) |

 (8.32)
(8.32)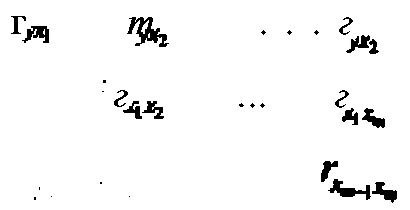
 (8.33)
(8.33) (8.34)
(8.34) (8.35)
(8.35) (8.36)
(8.36) (8.37)
(8.37) (8.38)
(8.38)


