
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Эквивалентная схема тепловых проводимостейСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Рассмотрим метод расчёта температуры нагретой зоны прибора с перфорированным кожухом (рис. 6.21,а). Тепло рассеивается в окружающую среду путём конвекции и излучения наружными поверхностями кожуха, а также отбирается протекающим через прибор воздухом. Движение воздуха обусловлено разностью температур нагретых и холодных объёмов воздуха, а следовательно, и давлений внутри и снаружи прибора. Воздух втекает в блок через нижние отверстия 1 кожуха, при этом нагревается, плотность его становится меньше. Поднимаясь вверх, воздух проходит через отверстия шасси, попадает в верхнюю область и далее через отверстия 2, расположенные в верхней части, выходит наружу. Между мощностью, рассеиваемой в приборе, температурой отдельных частей, геометрическими и физическими параметрами конструкции и условиями эксплуатации должна существовать зависимость. Задача состоит в том, чтобы найти эту зависимость [17,7]. Чтобы упростить задачу, сделаем ряд допущений: 1. Будем считать, что нижняя поверхность шасси делит внутренний объем прибора на две равные части с температурами
где
Это допущение сделано в предположении, что температура воздуха, протекающего через соответствующий объём, меняется линейно. 2. Нагрев воздуха внутри прибора происходит только за счёт конвекции, для лучистой энергии воздух прозрачен, и его нагревания за счёт лучеиспускания не происходит. 3. Коэффициент теплоотдачи всех внутренних поверхностей прибора будем считать одинаковым. 4. Кожух и нагретую зону будем считать изотермическими поверхностями. В соответствии с принятыми допущениями можно выделить пять изотермических областей: нагретую зону
Применяя закон сохранения энергии к отдельным процессам теплообмена прибора с перфорированным кожухом, можно составить систему уравнений, решая которую, найдём связь между температурой отдельных областей прибора и физическими и геометрическими параметрами конструкции. Первое уравнение запишем из условия, что тепловая энергия, передаваемая конвекцией воздуху от нижней поверхности шасси и от нижней части кожуха (нижняя область), идёт на повышение теплосодержания воздуха:
или иначе –
где
Правая часть уравнения (6.53) записана на основании допущения 1. Изменение теплосодержания воздуха в нижней области пропорционально разности температур (
В уравнение (6.58) входят четыре неизвестных: Второе уравнение получим из условия, что тепловая энергия, передаваемая конвекцией воздуху от верхней поверхности шасси и от верхней внутренней поверхности кожуха, идёт на повышение теплосодержания воздуха в области 2:
или
где Правая часть уравнения (6.56) составлена в предположении, что изменение теплосодержания воздуха в верхней области пропорционально разности температур
Из равенства (6.59) следует, что
поэтому
В уравнение (6.56) вошёл новый неизвестный параметр Третье уравнение составим исходя из условия, что мощность
или
Расчет
где Расчёт
При расчёте
где Увеличение расчётной поверхности кожуха приводит к некоторой неточности в определении Четвёртое уравнение может быть выведено из условия общего теплового баланса. Полная мощность источников энергии Р, расположенных в нагретой зоне, рассеивается наружной поверхностью кожуха, а часть тепла уносится проходящим через прибор воздухом, поэтому
Второе слагаемое правой части уравнения (6.64) составлено на основании допущения 1. Тепловая мощность, отводимая протекающим через прибор воздухом, пропорциональна разности температуры входящего и выходящего воздуха
Система из четырёх уравнений (6.53), (6.56), (6.60) и (6.64) содержит пять неизвестных: Для определения пятого уравнения необходимо проанализировать условия теплообмена в приборе. Связь между количеством воздуха G, протекающего в единицу времени через отверстия 1 на рис. 6.21, площадь которых
где Аналогичные выражения можно получить для воздуха, протекающего в единицу времени через отверстия в шасси и в верхней части кожуха:
где В установившемся режиме расход воздуха через любые сечения кожуха и шасси одинаков:
За начальный уровень отсчёта давлений принимается уровень, проходящий через середину отверстий 1. Наружное избыточное давление воздуха относительно этого уровня
Давление воздуха внутри прибора на уровне отверстий 2 относительно уровня отсчёта
где Давление воздуха снаружи прибора на уровне отверстий 2
Напор в отверстии 2
Сгруппируем все перепады давлений в левую часть. С учётом того что
Масса воздуха, проходящего в единицу времени через нижние отверстия шасси и верхние отверстия, одинакова, поэтому
Приравнивая попарно и возводя в квадрат, получим
Выразим плотность воздуха в области 1 и 2 через абсолютную температуру:
Подставим
Подставив (6.77) в (6.66), получим расход воздуха через прибор В результате преобразования системы уравнений (6.53), (6.55), (6.60), (6.64) получаем уравнения для практических расчетов: 1) здесь
2) 3) Система уравнений (6.78) - (6.81) позволяет рассчитать тепловые характеристики Коэффициент расхода
Таблица 6.7 Зависимость коэффициента
Коэффициент теплоотдачи Если перфорационных отверстий в кожухе много и они расположены на разной высоте от шасси, то параметры
где 1i и 2i – номер отверстия в нижней и верхней областях прибора.
|
||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-29; просмотров: 495; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.134.245.35 (0.013 с.) |

 и
и  , т. е. температура внутри данной области не меняется и равна среднеарифметическому значению температур входящего и выходящего воздуха
, т. е. температура внутри данной области не меняется и равна среднеарифметическому значению температур входящего и выходящего воздуха (6.50)
(6.50) (6.51)
(6.51) - температура воздуха вблизи нижней поверхности шасси;
- температура воздуха вблизи нижней поверхности шасси;  - температура вытекающего из прибора воздуха.
- температура вытекающего из прибора воздуха. ; кожух
; кожух  ; воздух в нижней части
; воздух в нижней части 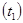 ; воздух в верхней части
; воздух в верхней части 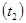 ; окружающую среду
; окружающую среду 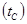 . Эквивалентная схема теплового процесса представлена на рис. 6.21,б. Тепловая мощность Р, выделяемая в нагретой зоне, рассеивается тремя путями: конвективно передается кожуху в нижней и верхней части прибора и излучением – кожуху. Кожух наружной поверхностью рассеивает тепловую энергию в окружающую среду конвекцией и излучением. С внутренней поверхности кожуха тепло конвекцией передается воздуху, протекающему внутри прибора. Воспринимаемое воздухом тепло идет на повышение его теплосодержания, поэтому точки эквивалентной схемы с температурой
. Эквивалентная схема теплового процесса представлена на рис. 6.21,б. Тепловая мощность Р, выделяемая в нагретой зоне, рассеивается тремя путями: конвективно передается кожуху в нижней и верхней части прибора и излучением – кожуху. Кожух наружной поверхностью рассеивает тепловую энергию в окружающую среду конвекцией и излучением. С внутренней поверхности кожуха тепло конвекцией передается воздуху, протекающему внутри прибора. Воспринимаемое воздухом тепло идет на повышение его теплосодержания, поэтому точки эквивалентной схемы с температурой 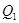 и
и  .
. (6.52)
(6.52)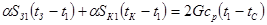 , (6.53)
, (6.53) - конвективный коэффициент теплоотдачи всех внутренних поверхностей прибора;
- конвективный коэффициент теплоотдачи всех внутренних поверхностей прибора; - площадь реальной поверхности нагретой зоны в области 1;
- площадь реальной поверхности нагретой зоны в области 1;  - площадь поверхности кожуха в нижней области; G – расход воздуха, протекающего через нижнюю область 1,
- площадь поверхности кожуха в нижней области; G – расход воздуха, протекающего через нижнюю область 1,  ;
;  - удельная теплоёмкость воздуха при постоянном давлении,
- удельная теплоёмкость воздуха при постоянном давлении,  .
.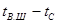 ), которая с учётом уравнения (6.50) будет
), которая с учётом уравнения (6.50) будет . (6.54)
. (6.54)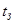 ,
, 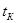 ,
,  (6.55)
(6.55) , (6.56)
, (6.56) - площадь поверхности нагретой зоны в области 2;
- площадь поверхности нагретой зоны в области 2;  - площадь поверхности кожуха в верхней области.
- площадь поверхности кожуха в верхней области. , которая с учётом уравнения (6.51) будет
, которая с учётом уравнения (6.51) будет . (6.57)
. (6.57) ,
, . (6.58)
. (6.58) источников тепла передается излучением от нагретой зоны к кожуху. От кожуха тепло
источников тепла передается излучением от нагретой зоны к кожуху. От кожуха тепло  отводится в двух направлениях: внутрь прибора, нагревая находящийся в нём воздух путём конвекции, и в окружающее пространство:
отводится в двух направлениях: внутрь прибора, нагревая находящийся в нём воздух путём конвекции, и в окружающее пространство: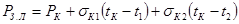 (6.59)
(6.59) . (6.60)
. (6.60) , (6.61)
, (6.61)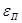 - приведенная степень черноты нагретой зоны и внутренней поверхности кожуха;
- приведенная степень черноты нагретой зоны и внутренней поверхности кожуха;  - площадь поверхности нагретой зоны;
- площадь поверхности нагретой зоны; 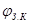 - коэффициент взаимной облучённости нагретой зоны и внутренней поверхности кожуха; если пренебречь отверстиями в кожухе, то можно считать
- коэффициент взаимной облучённости нагретой зоны и внутренней поверхности кожуха; если пренебречь отверстиями в кожухе, то можно считать 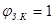 .
.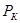 производится по формуле
производится по формуле  . Тепловая проводимость
. Тепловая проводимость 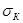 от кожуха в окружающую среду определяется выражением
от кожуха в окружающую среду определяется выражением . (6.62)
. (6.62)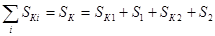 , (6.63)
, (6.63) - площадь поверхности кожуха, без учёта перфорации;
- площадь поверхности кожуха, без учёта перфорации;  и
и  - общая площадь отверстий на кожухе, расположенных соответственно ниже и выше шасси.
- общая площадь отверстий на кожухе, расположенных соответственно ниже и выше шасси. и
и  . Это допущение значительно упрощает дальнейшие рассуждения.
. Это допущение значительно упрощает дальнейшие рассуждения. . (6.64)
. (6.64)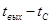 . На основании уравнений (6.57) и (6.58) можно написать
. На основании уравнений (6.57) и (6.58) можно написать . (6.65)
. (6.65)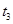 , G и
, G и  снаружи и внутри прибора на уровне отверстий 1 выражается формулой
снаружи и внутри прибора на уровне отверстий 1 выражается формулой (6.66)
(6.66) - коэффициент расхода (если жалюзи отсутствуют и имеются только отверстия, то
- коэффициент расхода (если жалюзи отсутствуют и имеются только отверстия, то  - см. табл. 6.7); g – ускорение силы тяжести;
- см. табл. 6.7); g – ускорение силы тяжести; 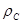 - плотность воздуха при температуре
- плотность воздуха при температуре 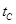 .
. ; (6.67)
; (6.67) ; (6.68)
; (6.68) - коэффициенты расхода через отверстия в шасси и в верхней части кожуха соответственно;
- коэффициенты расхода через отверстия в шасси и в верхней части кожуха соответственно;  - площадь отверстий в шасси;
- площадь отверстий в шасси;  - плотность воздуха при температуре
- плотность воздуха при температуре  - разность давлений воздуха между верхней и нижней областями в районе шасси;
- разность давлений воздуха между верхней и нижней областями в районе шасси; 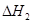 - разность давлений воздуха снаружи и внутри прибора на уровне отверстий 2 (см. рис. 6.21).
- разность давлений воздуха снаружи и внутри прибора на уровне отверстий 2 (см. рис. 6.21). . (6.69)
. (6.69) , а внутри нижнего отсека
, а внутри нижнего отсека  . Тогда напор в отверстии 1 будет
. Тогда напор в отверстии 1 будет . (6.70)
. (6.70) , (6.71)
, (6.71) и
и  - расстояние от шасси до середины соответствующего отверстия 1 и 2.
- расстояние от шасси до середины соответствующего отверстия 1 и 2. . (6.72)
. (6.72) . (6.73)
. (6.73)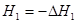 , получим
, получим . (6.74)
. (6.74)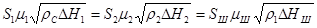 .
.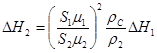 ;
;  . (6.75)
. (6.75) ;
; 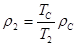 . (6.76)
. (6.76) . (6.77)
. (6.77) . (6.78)
. (6.78) ; (6.79)
; (6.79) ;
; ;
; ;
; ;
;  ;
;  ;
; ;
;  ;
; ; (6.80)
; (6.80) . (6.81)
. (6.81)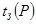 и
и  . Для этого необходимо знать расход воздуха G, коэффициент расхода
. Для этого необходимо знать расход воздуха G, коэффициент расхода  и коэффициент теплоотдачи
и коэффициент теплоотдачи  и углах открытия
и углах открытия  .
.

 ;
;  ,
,


