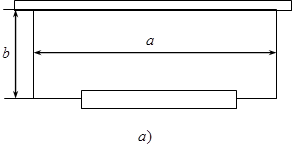Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Конструктивные способы защиты приборной аппаратуры от механических воздействийСодержание книги
Поиск на нашем сайте
Вибро- и ударозащита конструкций АПА с помощью амортизаторов, применяется в конструкциях второго и третьего уровней (блоки, стойки). Это обусловлено тем, что номинальная нагрузка даже легких амортизаторов может быть обеспечена, начиная с уровня блока, а конструктивно потери за счет увеличения массы и объема конструкции становятся незначительными. В тоже время, ряд эффективных мер защиты конструкций от механических воздействий может быть применен на уровне функциональных узлов и микросборок с целью повышения демпфирующих свойств жесткости конструкции. При конструировании микросборок предусматривается вибро- и удароизоляция компонентов. Для уменьшения коэффициента передачи механических воздействий, приложенных к подложке, компоненты закрепляются на подложке с помощью вибропоглощающего клея. После полимеризации клей остается эластичным, поэтому система "компонент-клеевая прослойка- подложка" может быть представлена моделью механической колебательной системы с кинематическим возбуждением (рис. 5.2,в). Перечень применяемых клеев достаточно широк, но чаще всего используются клеи ВК-9, КВК-68, МК-400. Повышению вибропрочности микросборок способствует ограничение длины гибких выводов компонентов и проволочных перемычек. Проволочный вывод компонента и перемычка могут быть представлены моделью балки круглого сечения с жестким закреплением на концах. Поэтому ограничение на длину балки является ограничением снизу частоты свободных колебаний из условия вибропрочности конструкции. Допустимая длина вывода (перемычки между двумя точками закрепления) определяется из неравенства На структурном уровне функциональных узлов устойчивость конструкций к механическим воздействиям достигается за счет использования вибропоглощающих адгезионных материалов и сред, а также за счет различных способов повышения жесткости конструкций. Так, например, для уменьшения амплитуды резонансных колебаний печатных плат применяются вибропоглощающие слои. Коэффициент динамичности печатной платы, состоящей из трех слоев стеклотекстолита с вибропоглощающими прокладками между слоями, снижается примерно в восемь раз без заметного увеличения массы и габаритов. Другим примером применения вибропоглощающих слоев служит конструкция односторонней функциональной ячейки на бескорпусных микросборках. Микросборки и печатная плата закрепляются на металлической рамке с помощью демпфирующего компаунда КТ-102. Заливка узла со стороны радиокомпонентов вибропоглощающим пенополиуретаном снижает амплитуду резонансных колебаний более чем в 10 раз. Ухудшение ремонтопригодности и условий теплообмена таких конструкций можно в значительной мере исключить, применяя. слои сложной конфигурации, обеспечивающие неполное покрытие компонентов и доступ к отдельным точкам платы. Повышение жесткости конструкций ведет к смещению спектра частот свободных колебаний за верхнюю границу диапазона частот внешних колебаний и позволяет исключить резонансные явления. Для полного устранения резонансных колебаний необходимо, чтобы частота свободных колебаний основного тона была не менее чем на октаву выше верхней частоты внешних колебаний, т.е. Управлять жесткостью конструкций функциональных узлов можно выбором способа закрепления плат, подбором геометрических размеров, применением в конструкциях ребер жесткости, обечаек, рамок. Связь способа закрепления пластин и частоты свободных колебаний устанавливается формулами (5.8) и (5.9) через параметры Зависимость частоты свободных колебаний прямоугольной пластины от размера сторон иллюстрируется графиком на рис. 5.13. График построен для пластины с отношением сторон а/b=1 при свободном опирании по всем сторонам (частотная постоянная С = 45,8 и толщина пластины h=1,0 мм. Начальный размер пластины На рис. 5.14 приведена зависимость относительного изменения частоты свободных колебаний той же пластины от отношения сторон
Рис. 5.1. Ударный импульс: а – форма реального ударного импульса; б – эквивалентные формы
Рис. 5.2. Модели механических систем: а – расчетная модель с одной степенью свободы; б – расчетная модель с n-степенями свободы; в – модель колебательной системы с кинематическим возбуждением
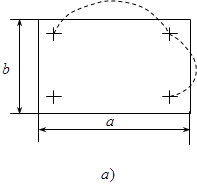
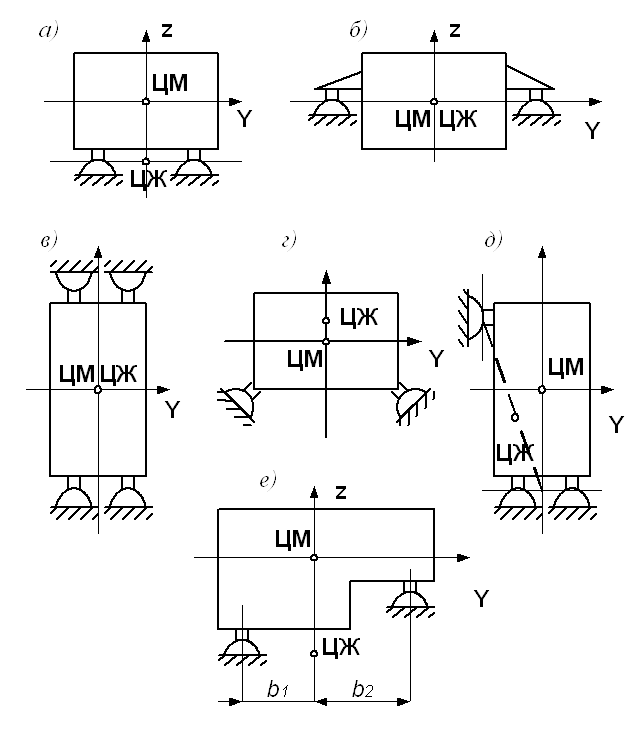
Рис. 5.3. Построение расчетной модели платы, закрепленной в четырех точках по углам: a – конструкционная модель; б – расчетная модель
Рис. 5.4. Построение расчетной модели платы, закрепленной в шести точках по контуру: a – конструкция платы; б – расчетная модель
Рис. 5.5. Построение расчетной модели функционального узла разъемного типа: а – конструкция платы; б – расчетная модель
Рис. 5.6. К расчету момента инерции сечения рамки
Рис. 5.7. Конструкции амортизаторов: а – «ножка» (АН); б – с воздушным демпфированием (АД); в – пространственного нагружения (АПН); г – пружинно-сетчатый амортизатор; 1 – бобышка; 2 – стопорное кольцо; 3 – резиновое кольцо; 4 – крышка; 5 – баллон; 6 – пружина; 7 – прокладка; 8 – корпус; 9 – основание; 10 – ограничитель; 11 – фрикционные сухари; 12 – шайбы; 13 – винт; 14 – распорное кольцо; 15 – направляющая; 16 – сетчатая подушка; 17 – крышка
Рис. 5.8. Варианты монтажа амортизаторов: а, б, в, г, е – схемы рационального монтажа; д – комбинированная схема
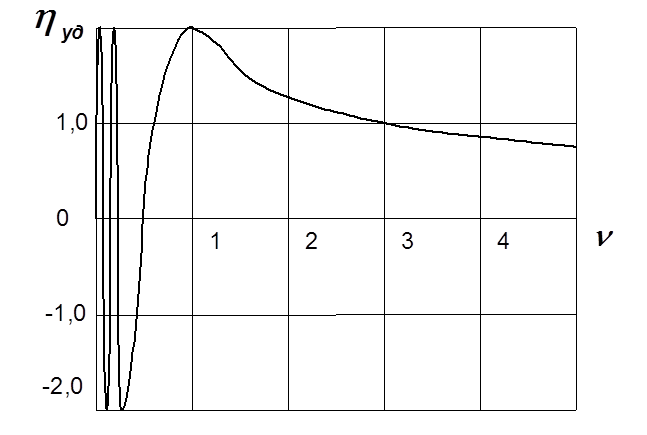
Рис. 5.9. Зависимость коэффициента передачи вибрации от частотной расстройки
Рис. 5.10. Закон изменения ускорения при воздействии синусоидального ударного импульса
Рис. 5.11. Зависимость коэффициента удароизоляции от частотной расстройки при синусоидальном ударном импульсе
Рис. 5.12. Зависимость коэффициента удароизоляции от частотной расстройки при ударном импульсе прямоугольной формы
Рис. 5.13. Зависимость частоты свободных колебаний платы от размеров сторон: а/b = 1; c = 45,8; a = 100 мм; h = 1 мм
Рис. 5.14. Зависимость частоты свободных колебаний пластины от отношения сторон: а Н =100 мм
Рис. 5.15. Зависимость нормированной массы и жесткости пластины от ее толщины: Е = 30,2 . 109 Н/м 2; Q = 1,85 . 103 кг/м 3 ; e = 0,22; hH = 0,5 мм
|
|||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-29; просмотров: 928; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.119 (0.009 с.) |

 , где d - диаметр вывода. Перемычка монтируется без натяжения, однако начальный ее прогиб (консольность) не должна превышать 10d.
, где d - диаметр вывода. Перемычка монтируется без натяжения, однако начальный ее прогиб (консольность) не должна превышать 10d.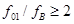 .
. и С соответственно. Количественную оценку этой связи можно получить из табл.5.1 и 5.2. Так, например, из данных табл. 5.2 следует, что для пластины с отношением сторон а/b=1 переход от свободного опирания к жесткому закреплению со всех сторон, ведет к росту частотной постоянной С приблизительно в 1,8 раза. Для других отношений сторон значение С возрастает примерно в 2,1 раза.
и С соответственно. Количественную оценку этой связи можно получить из табл.5.1 и 5.2. Так, например, из данных табл. 5.2 следует, что для пластины с отношением сторон а/b=1 переход от свободного опирания к жесткому закреплению со всех сторон, ведет к росту частотной постоянной С приблизительно в 1,8 раза. Для других отношений сторон значение С возрастает примерно в 2,1 раза. Н=100 мм. Из графика видно, что частота свободных колебаний уменьшается в четыре раза при увеличении размера стороны в два раза.
Н=100 мм. Из графика видно, что частота свободных колебаний уменьшается в четыре раза при увеличении размера стороны в два раза. . Нормирование частоты произведено относительно начального значения
. Нормирование частоты произведено относительно начального значения  для
для 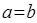 =100 мм. Толщина пластины h пересчитывается в частоту свободных колебаний через нормированную относительно площади массу m0 и цилиндрическую жесткость D. При увеличении толщины пластины масса m0 возрастает линейно, а цилиндрическая жесткость – пропорционально h3. Зависимости m0/ m0Н (прямая 1) и D/DH (кривая 2) от относительного изменения толщины пластины (hH=0.5мм) из фольгированного стеклотекстолита (Е= 30,2 • 109 Па,
=100 мм. Толщина пластины h пересчитывается в частоту свободных колебаний через нормированную относительно площади массу m0 и цилиндрическую жесткость D. При увеличении толщины пластины масса m0 возрастает линейно, а цилиндрическая жесткость – пропорционально h3. Зависимости m0/ m0Н (прямая 1) и D/DH (кривая 2) от относительного изменения толщины пластины (hH=0.5мм) из фольгированного стеклотекстолита (Е= 30,2 • 109 Па,  ,
,  ) приведены на рис. 5.15. Частота свободных колебаний пластины возрастает пропорционально h, относительное изменение частоты
) приведены на рис. 5.15. Частота свободных колебаний пластины возрастает пропорционально h, относительное изменение частоты  от толщины пластины соответствует прямой 1.
от толщины пластины соответствует прямой 1.