Общий случай отвода тепла от прибора
Рассмотрим расчёт теплового режима одиночного блока, в котором охлаждение происходит за счёт конвекции и лучеиспускания, а шасси дополнительно охлаждается протекающей по трубке жидкостью (рис. 6.15) [7].
Для начала предположим, что кожух не имеет жалюзи и перфорации, т. е. отсутствует сток тепла за счёт протекающего воздуха. Нагретую зону представим как изотермическую поверхность. Это допущение позволяет считать, что все источники тепловыделения в нагретой зоне распределены равномерно.
Будем, кроме того, считать, что известна суммарная мощность источников P, задана температура окружающей среды 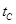 и температура втекающей в блок жидкости и температура втекающей в блок жидкости 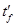 , а также известны все геометрические размеры конструкции ПА. , а также известны все геометрические размеры конструкции ПА.
Составим систему уравнений теплового баланса. Мощность P, выделяемая источниками тепловыделения, частично передаётся жидкости (Q), а частично – кожуху и рассеивается в окружающую среду 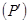 : :
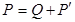 . (6.26) . (6.26)
Тепловой поток от стенок трубок к жидкости
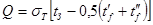 , (6.27) , (6.27)
где 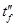 - температура вытекающей из блока жидкости; - температура вытекающей из блока жидкости; 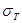 - тепловая проводимость участка между нагретой зоной и жидкостью. - тепловая проводимость участка между нагретой зоной и жидкостью.
Здесь предполагается, что температура стенок трубок равна средней температуре нагретой зоны и температура жидкости по длине трубки меняется линейно, т. е. средняя температура жидкости 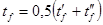 . .
Тепловой поток от нагретой зоны к кожуху выразим через тепловую проводимость 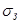 : :
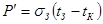 , (6.28) , (6.28)
где 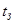 - средняя температура нагретой зоны; - средняя температура нагретой зоны; 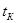 - температура кожуха. - температура кожуха.
Подставим эти выражения в (6.26):
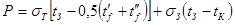 . (6.29) . (6.29)
Количество тепловой энергии Q, воспринимаемое в единицу времени жидкостью, идёт на повышение её теплосодержания:
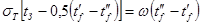 . (6.30) . (6.30)
Здесь 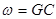 ; ; 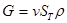 ; ; 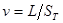 , где G и L – массовый и объёмный расход жидкости; C – удельная теплоёмкость жидкости при постоянном давлении, , где G и L – массовый и объёмный расход жидкости; C – удельная теплоёмкость жидкости при постоянном давлении,  ; ;  - плотность жидкости, кг/м3; v – скорость движения жидкости, м/с; - плотность жидкости, кг/м3; v – скорость движения жидкости, м/с; 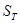 - площадь поперечного сечения трубки, м2. - площадь поперечного сечения трубки, м2.
Количество энергии, передаваемое в единицу времени от нагретой зоны кожуху и рассеиваемое в окружающую среду
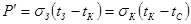 , (6.31) , (6.31)
где 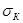 - тепловая проводимость участка между кожухом и средой. Решая систему уравнений (6.29), (6.30), (6.31) относительно - тепловая проводимость участка между кожухом и средой. Решая систему уравнений (6.29), (6.30), (6.31) относительно 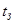 , , 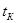 , , 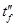 , получаем , получаем
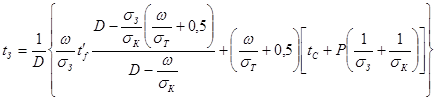 ; (6.32) ; (6.32)
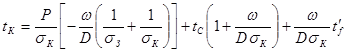 ; (6.33) ; (6.33)
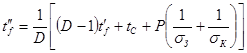 , (6.34) , (6.34)
где
 . (6.35) . (6.35)
Из выражений для 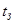 , , 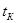 и и 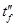 можно получить формулы для расчета теплового режима в двух предельных случаях: при отсутствии охлаждающей жидкости и при отсутствии кожуха. Если нет охлаждающей жидкости, это означает, что можно получить формулы для расчета теплового режима в двух предельных случаях: при отсутствии охлаждающей жидкости и при отсутствии кожуха. Если нет охлаждающей жидкости, это означает, что 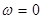 и и 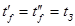 ; уравнения при этом принимают вид ; уравнения при этом принимают вид
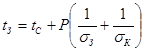 ; (6.36) ; (6.36)
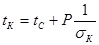 . (6.37) . (6.37)
Отсюда легко найти связь между температурой нагретой зоны и кожуха:
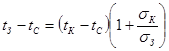 . (6.38) . (6.38)
Если в блоке отсутствует кожух, то 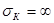 и тогда и тогда
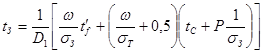 ; (6.39) ; (6.39)
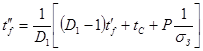 , (6.40) , (6.40)
где
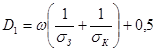 . (6.41) . (6.41)
Здесь 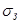 - тепловая проводимость участка между нагретой зоной и окружающей средой. - тепловая проводимость участка между нагретой зоной и окружающей средой.
Используя выражения для температуры нагретой зоны и температуры кожуха, можно перейти к расчёту конкретных конструкций. При выводе этих выражений предполагалось, что тепловые проводимости 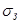 , , 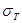 и и 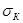 являются постоянными. На самом деле всё обстоит значительно сложнее. Каждая тепловая проводимость будет зависеть от искомой температуры, поэтому прямым путём эта задача не решается и необходимо воспользоваться методом последовательных приближений. являются постоянными. На самом деле всё обстоит значительно сложнее. Каждая тепловая проводимость будет зависеть от искомой температуры, поэтому прямым путём эта задача не решается и необходимо воспользоваться методом последовательных приближений.
|