Методика изучения нумерации чисел концентре «Многозначные числа»

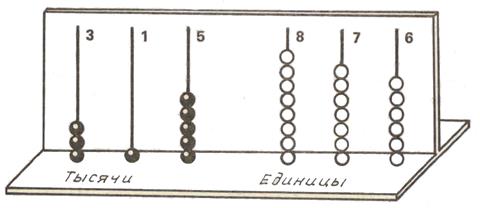
Общие положения. Изучая материал концентров «Десяток», «Сотня», «Тысяча», учащиеся ознакомились с цифрами десятичной системы счисления, разрядами единиц, десятков, сотен. Сейчас же им предстоит усвоить понятие классов чисел. Это понятие позволяет перейти к нумерации сколь угодно больших натуральных чисел. Поэтому в концентре «Многозначные числа» заканчивается изучение нумерации целых неотрицательных чисел.

В предыдущих концентрах учащиеся запоминали таблицу сложения (вычитания), умножения (деления), овладевали приемами устного выполнения этих операций, приемами письменного сложения и вычитания. В концентре «Многозначные числа» эти знания и умения обобщаются для компонентов, имеющих более трех цифр. Здесь же ученики овладевают алгоритмами письменного умножения и деления — самыми сложными в курсе математики начальной школы.

Нумерация. При изучении нумерации многозначных чисел удобно использовать нумерационную таблицу, которая заполняется карточками с цифрами:

Класс миллионов Класс тысяч Класс единиц разряд сотен разряд десятков разряд единиц разряд сотен разряд десятков разряд единиц разряд сотен разряд десятков разряд единиц

Возможно, что некоторые учащиеся встретятся с трудностями при изучении нумерации многозначных чисел, обобщении приемом письменного сложения и вычитания. Поэтому в качестве наглядного пособия используется позиционный абак, который имеет уже не три, а шесть или девять спиц.

Изучение нумерации многозначных чисел следует предварить краткой, но яркой беседой о значении больших чисел. Нужно показать учащимся, что без использования таких больших чисел, как миллион, сотни тысяч, невозможно выразить количество той или иной продукции. Переходя к изучению нумерации, необходимо вспомнить некоторые свойства позиционной системы счисления:

1) значение цифры в числе определяется ее местом в этом числе;

2) названия чисел, обозначаемых одной, двумя и тремя цифрами, образуются по определенным правилам;

3) прибавление к 9 единицам еще одной единицы данного разряда дает единицу следующего, более старшего разряда.

Для этого учащимся предлагаются, например, такие упражнения (для устного счета).

1. Что означает цифра 3(5, 7) в числах 537; 735; 375? Сколько единиц каждого разряда в числах 573; 872, 670 и т. д.?

Сколько сотен, десятков, единиц в числах 674; 609; 70 и т. д.?

Какое число содержит 6 сотен; 8 десятков; 54 десятка; 2 сотни, 6 десятков и 4 еди­ницы; 2 сотни и 8 единиц и т. д.?

В виде суммы каких разрядных слагаемых можно представить числа 823; 321; 149; 303 и т. д.?

2. Длина отрезка 15 мм. Как по-другому можно выразить его длину? Как можно выразить длину отрезка в 206 см; 29 дм; 400 см; 400 дм и т. д.?

Как называется число, в котором 10 десятков; 10 сотен; 60 десятков и т. д.?

3. К 9 единицам прибавили единицу; к 8 десяткам прибавили 2 десятка; к 4 сотням прибавили 6 сотен и т. д. Как называются полученные числа?

При изучении нумерации многозначных чисел можно выделить дна этапа. Сначала учащиеся учатся называть и записывать многозначные числа, не имеющие единиц в разрядах класса единиц, т. е. числа, оканчивающиеся тремя нулями. Вспомним, как начиналось знакомство учащихся с нумерацией чисел в пределах 100, 1000. Рассматривались соответственно понятия «десяток», «сотня». Десяток и сотня использовались затем как счетные единицы.

Первые числа класса тысяч образуются в результате счета тысячами: одна тысяча, две тысячи,..., десять тысяч. Одновременно заполняется косточками спица тысяч абака. При получении 10 тысяч, согласно правилу работы с абаком, десять косточек на спице тысяч заменяются одной косточкой на спице более старшего разряда — десятков тысяч.

Далее счет продолжается уже десятками тысяч: десять тысяч, двадцать тысяч,..., сто тысяч. На соответствующую спицу абака последовательно нанизываются косточки. Когда их оказывается десять, они заменяются одной косточкой, которая нанизывается на спицу более старшего разряда — сотен тысяч.

Затем учащиеся считают сотнями тысяч. Одновременно заполняется соответствующая спица абака. Как только на ней появляется 10 косточек, все они заменяются одной косточкой на следующей спице. Число, которое эта косточка обозначает, называется миллионом.

Таким образом, ученики знакомятся с названиями новых разрядов: единиц тысяч, десятков и сотен тысяч и учатся заполнять соответствующие спицы абака.

Далее учащиеся учатся называть числа вида 11 тысяч, 24 тысячи, 347 тысяч и т. д. Для этого используются следующие упражнения. На спицы единиц, десятков и сотен тысяч абака нанизаны соответственно 5, 3 и 7 косточек. Спрашивается, какое число изображено на абаке. Учащиеся рассуждают: в этом числе 7 сотен ты­сяч, 3 десятка тысяч и 5 тысяч. Учитель объявляет, что такое число называется семьсот тридцать пять тысяч.

Одновременно учащиеся работают над упражнениями другого рода: называется число, обозначающее некоторое количество тысяч, нужно отложить соответствующее количество косточек на спицах абака.

В процессе такой работы школьники должны увидеть сходство в образовании названий чисел первого и второго класса: для единиц тысяч не существует специальных названий, они называются так же, как единицы первого класса, но с прибавлением слова «тысяча»; нет специальных названий и для десятков тысяч: для них используются названия десятков первого класса с прибавлением слова «тысяча» и т. д.

Для закрепления этих знаний может быть составлена, например, следующая таблица:

10 единиц — десяток 10 тысяч — десяток тысяч

100 единиц — сотня 100 тысяч — сотня тысяч

100 единиц— 10 десятков 100 тысяч — 10 десятков тысяч

Вместе с тем важно показать различие между одноименными разрядами классов единиц и тысяч. Для этого на абаке откладываются, например, числа: 120 тысяч и 120, 50 тысяч и 50, 178 тысяч и 178. Обсуждается сходство и различие в изображении этих чисел. Сходство состоит в том, что на спицах соответствующих разрядов класса единиц и тысяч отложены одинаковые количества косточек. Однако 8 косточек для числа 178 означает количество единиц в разряде единиц, а для числа 178 тысяч — количество тысяч в разряде единиц тысяч.

Далее учащиеся записывают многозначные числа, оканчиваю­щиеся тремя нулями. В изображении числа 5 тысяч на абаке в младших разрядах отсутствуют косточки. Это означает, что в этих разрядах 0 единиц. Обозначение этого числа цифрами выполняется в нумерационной таблице. В связи с использованием этой таблицы вводится понятие «класс», еще раз обсуждается сходство и разли­чие в значении разрядов разных классов.

После заполнения абака и таблицы учащиеся записывают данное число в тетрадях. Для удобства записи многозначного числа между группами цифр разных классов оставляется промежуток (например, клетка тетради).

Аналогично приходят к записи чисел вида 700 тысяч, 107 тысяч, 420 тысяч, 567 тысяч и т. д. Основным средством наглядности при этом является нумерационная таблица.

Одновременно с изучением нумерации можно рассмотреть приемы устного сложения и вычитания многозначных чисел. Эти приемы основаны на знании учащимися разрядного состава многозначных чисел и применимы лишь в случаях следующего вида: 200 000 + 300 000, 100 000 + 50 000 + 7 000, 600 000 - 400 000, 350 000 - 50 000, 342 000 - 42 000 и т. д. Вычисления при необходимости легко иллюстрируются с помощью абака и нумерационной таблицы. Устное вычисление значений таких выражений способствует усвоению нумерации и подготавливает учащихся к выполнению письменного сложения и вычитания многозначных чисел.

Умножение и деление вида 5 000 · 2, 80 000: 4, 17 000 · 3, 150 000: 5 не требует специального приема и целиком опирается на знание учащимися названий соответствующих многозначных чисел и таблицы умножения и деления, приемов устного умножения и деления.

Вместе с тем эпизодическое решение таких примеров облегчает усвоение нумерации, изучение последующих тем, связанных с умножением многозначных чисел.

С нумерацией остальных многозначных чисел учащихся можно ознакомить в процессе прибавления к многозначным числам, оканчивающимся тремя нулями, чисел первого класса. На абаке откладывается многозначное число уже известного учащимся вида, например 315 000. На спицы разрядов первого класса нанизываются косточки, соответствующие числу, например 876 (см. рис). Учитель спрашивает, как записать число, получившееся в результате сложения 315 000 и 876. Ответ очевиден. Подобные числа демонстрируются на нумерационной таблице. Учащиеся учатся называть подобные числа: сначала называется число единиц второго класса, а затем первого класса. Таким образом, число 315 876 читается так: триста пятнадцать тысяч восемьсот семьдесят шесть.

Предлагаются и обратные упражнения: по названию числа выполнить его запись (возможно, с предварительным изображением его на абаке).

В связи с введением понятия класса в систему упражнений по отработке навыков устной и письменной нумерации целесообразно включать упражнения, требующие использования этого понятия. Это могут быть, например, такие задания: «Запишите (изобразите на своем абаке) число, в котором: 200 единиц первого класса и 60 единиц второго класса; 107 единиц класса единиц и 6 единиц класса тысяч; по две единицы в разряде десятков второго класса и в разряде сотен первого класса; 320 единиц класса тысяч и 2 единицы класса единиц» и т. д.

Наряду с такими упражнениями предлагаются и обратные: «Назови, к какому классу и разряду относится каждая цифра числа 356 789, 50 283 и т. д.».

Изучая нумерацию, учащиеся продолжают упражняться в устных вычислениях (сложении и вычитании) на множестве многозначных чисел: 350000 + 102, 200 018 + 600 100, 85007 - 80007, 150 120 - 50 100 и т. д.

Для расширенного множества чисел устанавливается справедливость отношения порядка. Учащиеся считают в прямом и обратном порядке, начиная с определенного числа; определяют числа, следующие непосредственно до и после данного числа. Например, им предлагается продолжить счет с 998 до 1005, с 7 589 до 7 600; присчитывать по единице к числам 99 989, 999 997; отсчитывать по одному от чисел 600 000, 100 000, 10 000, 7 000; назвать число, которое на 2 меньше, чем 40 000, и т. д.

Школьники должны научиться сравнивать многозначные числа. С помощью позиционной таблицы легко показать, что начинать
сравнивать два многозначных числа нужно с единиц второго класса. То число больше, у которого больше единиц второго класса.
Если их число одинаково, то сравнивается число единиц первого класса.

Увеличение и уменьшение числа в 10, 100 и 1 000 раз. Расширяя знания учащихся о десятичной системе счисления, можно ознакомить их с простым способом увеличения или уменьшения числа в 10, 100 и 1 000 раз, кратного сравнения чисел особого вида. Это необходимо для прочного усвоения ими позиционного принципа ну­мерации. Изложим методику изучения этого материала.

Учащимся предлагают рассмотреть ряд чисел и рассказать об их особенностях. Пусть этот ряд имеет вид: 3, 30, 300, 3 000, 30 000, 300 000. В числе обнаруженных особенностей могут быть такие: в каждом числе встречается цифра 3; все числа записаны с помощью одной цифры 3 или цифры 3 и нулей; цифра 3 в каждом числе обозначает разные разрядные единицы: единицы, десятки, сотни и т. д.

Предлагается последовательно сравнить эти числа парами.

3 и 30: 30 в 10 раз больше, чем 3, так как 30: 3= 10 (это учащимся известно из темы «Увеличение и уменьшение числа в несколько раз»);

30 и 300: эти числа можно представить в виде 3 десятка и 30 десятков; это позволит, как и в предыдущем случае, установить, что 30 десятков в 10 раз больше, чем 3 десятка, а значит, 300 в 10 раз больше, чем 30.

Аналогично устанавливается соотношение между парами 300 и 3 000, 3 000 и 30 000, 30 000 и 300 000.

Далее сравниваются числа 3 и 300. Случай 300: 3 рассматривался уже в концентре «Тысяча» - 300:3=100. А это, как известно, означает, что 300 в 100 раз больше, чем 3. Такие же соотношения устанавливаются и для чисел 30 и 3 000, 300 и 30 000, 3 000 и 300 000 (для этого они приводятся к виду 3 дес. и 300 дес, 3 сот. и 300 сот. и т. д.).

Вывод о том, что 3 000 в 1 000 раз больше, чем 3, делается по индукции. Этот вывод распространяется и на другие пары чисел. Затем следует обобщение: число, которое в 10 (100, 1 000) раз больше другого, имеет на один (два, три) нуль справа больше. На основании этого вывода делается заключение, что если у числа на один (два, три) нуль справа меньше, чем у другого числа, то оно в 10 (100 или 1 000) раз меньше другого числа.

Выполняются упражнения на закрепление: «Увеличь число 5 в 10, 100, 1 000 раз; число 80 — в 10, 100, 1 000 раз» и т. д.; «Уменьши число 300 в 10, 100 раз; число 70 000 — в 10, 100, 1 000 раз» и т. д.

Эти правила без каких-либо пояснений можно использовать для сравнения чисел 118 и 1 180, 27 и 27 000 и т. д.

Состав многозначных чисел. С целью подготовки учащихся к изучению алгоритмов письменного умножения и деления полезно научить их определять, сколько полных десятков, сотен, тысяч содержится в данном многозначном числе.

Ученики обладают некоторым опытом выполнения заданий такого рода: они умеют определять, сколько десятков в трехзначном числе. Это и используется в работе с многозначными числами.

Школьникам предлагается определить, сколько десятков в числе 3 576. Это число представляется в виде суммы разрядных слагаемых.

Последовательно выясняется, сколько десятков в каждом из этих слагаемых: 7, 50, 300. (Например, учащиеся рассуждают так; в 1000 - 10 сотен или 100 десятков, значит, в 3000—300 десятков.) В числе 3 576—357 десятков. Аналогично установили, что в этом числе 35 сотен. Если рассмотреть столь же подробно еще несколько чисел, то нетрудно заметить законо­мерность в определении состава числа.

Именованные числа. Большую помощь при изучении и усво­ении нумерации многозначных чисел оказывают упражнения с со­ставными именованными числами, выраженными в десятичных мерах. Эти числа дают возможность наглядно представить понятия разряда тысяч, десятков и сотен тысяч. Такие упражнения должны использоваться на всех этапах изучения нумерации. Например, когда учащиеся учатся определять состав многозначного числа, целесообразно выполнить такие упражнения: «Сколько дециметров в 3 576 см? Сколько километров составляют 3 576 м? Сколько килограммов в 12 070 г? Сколько рублей составляют 67 000 к?» и т. д. Основные положения методики обучения нумерации в пределах миллиона могут быть использованы и для знакомства учащихся с числами класса миллионов.