Нумерация чисел в пределах 100

Знакомство с числами от 21 до 100 начинают с устной нумерации. Образование и называние чисел 30; 40, 50, 60, 70, 80, 90, 100 объясняется в процессе счета десятками: 1 десяток — десять единиц, 2 десятка — двадцать единиц, 3 десятка — тридцать единиц, 4 десятка — сорок единиц, 5 десятков — пятьдесят единиц, шесть десятков — шестьдесят единиц, семь десятков — семьдесят единиц, восемь десятков — восемьдесят единиц, девять десятков — девяносто единиц, десять десятков — сто единиц. При введении и анализе названий десятков обращается внимание на то, что все они, кроме «сорок» и «сто», образованы по одному принципу. Правда, слово «десять» претерпело разные изменения в группе «двадцать-тридцать» и в группе «пятьдесят - шестьдесят - семьдесят - восемьдесят». На ранних ступенях развития русского языка вместо «сорок» и «сто» говорили «четыредесять» и «девятьдесять». Поясняя происхождение слова «сорок», полезно совершить экскурс в историю.

Освоив счет десятками, учащиеся знакомятся с образованием и именами любых чисел в пределах сотни: 2 десятка и 5 единиц — это двадцать пять; 4 десятка и 7 единиц — это сорок семь и т. п. Упражнения на образование чисел чередуются с упражнениями на разложение чисел: пятьдесят шесть — это 5 десятков и шесть единиц; девяносто один — это 9 десятков и 1 единица и т. п.

При изучении письменной нумерации учащиеся знакомятся с понятиями разряда и разрядного числа. Поясняется, что, например, тридцать семь — это 3 десятка и 7 единиц, но можно сказать и по-другому: 3 единицы второго разряда и 7 единиц первого разряда. Здесь полезно использовать карточки с разрядными числами, которые помогают усвоить состав числа, представить его в виде суммы разрядных слагаемых (56 = 50 + 6). Эти навыки затем используются при изучении операций над натуральными числами.

Изучая нумерацию в пределах 100, учащиеся выполняют упражнения на сложение и вычитание:

1) прибавление и вычитание числа 1;

2) прибавление к целому числу десятков однозначного числа;

3) вычитание всех десятков из числа;

4) прибавление целого числа десятков к однозначному числу;

5) вычитание всех единиц из числа.

Методика вычислений здесь та же, что и для подобных случаев в пределах 20. При выполнении упражнений на присчитывание и отсчитывание единицы, чисел, кратных 10, используется наглядное пособие «лента ста» — метровая лента с обозначенными сантиметрами и дециметрами.

Усвоению последовательности чисел первой сотни в натуральном ряду способствуют также следующие упражнения:

1) назовите число, предшествующее числу 27 (после какого числа при счете называют число 27?);

2) назовите число, следующее за числом 27 (перед каким числом при счете называют число 28?);

3) между какими числами называют при счете число 27?

Работа по усвоению нумерации продолжается и при изучении операций сложения и вычитания в пределах 100.

Итак, изучив нумерацию чисел в пределах 100, учащиеся должны усвоить: а) имена двузначных чисел в устной и письменной речи, их десятичный состав; б) расположение чисел до 100 в натуральном ряду; в) смысл терминов: «единица первого разряда», «единица вто­рого разряда», «разрядное число», «однозначное число», «двузначное число».

 

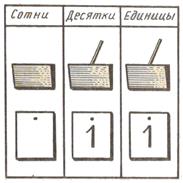
Методика изучения нумерации чисел в концентре «Тысяча»

Общие положения.

Известно, что наряду с концентрами «Десяток» и «Сотня» в начальном курсе математики выделяется концентр «Тысяча». Это объясняется тем, что при изучении трехзначных чисел учащиеся усваивают качественно новые сведения из области нумера­ции чисел и очень важные алгоритмы выполнения арифметических операций.

Изучая нумерацию трехзначных чисел, ученики знакомятся с новым разрядом — сотен. Тем самым завершается формирование класса единиц. Это позволяет в дальнейшем делать более крупные шаги в изучении нумерации: числа, большие тысячи, будут вводиться не по разрядам, а по классам.

При изучении концентра «Тысяча» расширяются знания учащихся об операциях сложения и вычитания. Они усваивают приемы письменного сложения и вычитания, которые впоследствии используются и на множестве многозначных чисел.

Нумерация чисел

При изучении нумерации чисел в пределах десяти естественными наглядными пособиями были множества реальных предметов, более абстрактные множества — палочек, геометрических фигур. Изучение нумерации в пределах ста потребовало более сложных пособий, например, таких, как абак. Однако для того чтобы изобразить, например, число 500, потребовался бы абак с 50 карманами. Поэтому при изучении нумерации сложения и вычитания в пределах тысячи используется позиционный абак. Особенность его состоит в том, что наглядный материал, изображающий единицы, десятки и сотни, имеет один и тот же вид — это или косточки счетов, или квадраты, или палочки. Зато карманы абака — их всего три - выполняют разные функции. Палочка, находящаяся в крайнем левом кармане (рис. 30), означает единицу.

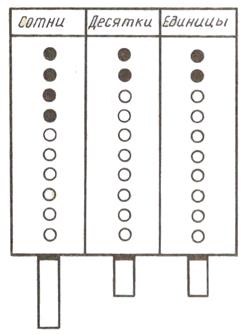
Если палочку положить в средний карман, она будет означать десяток, а если в крайний правый, - то сотню. Заметим, что принцип изображения чисел на непозиционном абаке был другим: карманам не приписывалось какое-либо определенное значение, а различались символы, которыми их заполняли.

Вместо абака, изображенного на рисунке, могут использоваться абаки других конструкций

 

Желательно, чтобы каждый учащийся имел абак для индивидуальной работы.

Другим важным наглядным пособием, используемым в концентре «Тысяча», является арифметический «ящик» или его модификации

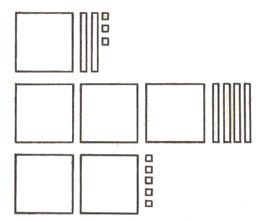
Такой ящик представляет собой набор элементов трех видов: кубики для изображения единиц; бруски, состоящие из 10 кубиков и служащие для обозначения десятков; пластины, состоящие из 10 брусков, обозначающих сотни. Десять пластин составляют куб — символ тысячи.

Для демонстраций у доски и индивидуальной работы удобен более простой вариант арифметического «ящика». Роль единиц играют квадраты, десятков — полоски, состоящие из 10 квадратов. Большие квадраты, состоящие из 10 полосок или 100 маленьких квадратов, служат для изображения сотен. Эти материалы могут быть изготовлены из плотной бумаги или картона.

Нумерация чисел от 10 до 100 изучалась в три приема: нумерация чисел второго десятка, круглых десятков, остальных двузначных чи­сел. Это объяснялось тем, что образование названий чисел второго десятка, круглых десятков и остальных двузначных чисел имеет
особенности.

Названия трехзначных чисел образуются либо из названия круглых сотен, либо из названия круглых сотен и двузначных или однозначных чисел в сочетании. Поэтому знакомство учащихся с нумерацией трехзначных чисел осуществляется в два приема. Сначала школьники учатся называть и записывать трехзначные числа, оканчивающиеся нулями, а потом остальные трехзначные числа.

Круглые сотни. Сущность методики знакомства учащихся с числами этого вида состоит, во-первых, в том, чтобы показать им, что считать сотнями можно так же, как единицами и десятками, и что любое число сотен в пределах десяти имеет особое название.

Вначале учащиеся подсчитывают количество квадратов, укладываемых по одному в наборное полотно: «Один, два,..., девять».

Затем в наборное полотно по одной укладываются полоски («десятки»). По мере заполнения полотна учащиеся считают: «Один десяток квадратов, два десятка квадратов,..., девять десятков квад­ратов». Обращается внимание, что количество квадратов можно называть по-другому: «Десять квадратов, двадцать,..., девяносто квадратов».

Рассматривается модель новой счетной единицы — больший квадрат (пластинка), состоящий из 10 полосок. Так как каждая полоска содержит 10 квадратов-единиц, то констатируется, что пластинка содержит 100 таких квадратов. Поэтому, когда в наборное полотно пластинки укладываются по одной, школьники считают: «Одна сотня квадратов, две сотни квадратов,..., девять сотен квадратов». Учитель говорит, что число квадратов в каждом из этих случаев можно назвать: сто, двести,..., девятьсот. Обращается внимание учащихся на особенности и сходство в названиях сотен: две-сти, три-ста, четыре-ста, пять-сот,..., девять-сот.

Одновременно с названием круглых сотен выполняются операции сложения и вычитания: 5 сот. + 3 сот.= 8 сот., 7 сот.—2 сот. = 5 сот. и т. д. С помощью наглядных пособий учащиеся учатся отвечать на вопросы: «Сколько десятков в сотне,..., какое число соответствует 20 десяткам, 50 десяткам, 6 сотням?» и т. д.

Устная нумерация трехзначных чисел. Параллельно с заучиванием учащимися названий круглых сотен начинается рабо­та над устной нумерацией остальных трехзначных чисел. Это свя­зано с тем, что при счете сотнями у учащихся может сложиться впечатление, что за числом сто, например, непосредственно следует двести, за двести — триста и т. д. Появление названий трехзнач­ных чисел происходит «естественно», при выполнении учениками упражнений такого вида: «Назови число квадратов, изображенных на наборном полотне»

 

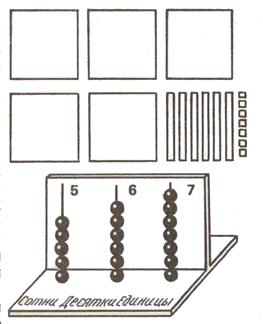
Учащиеся отвечают: «сто и два­дцать три», «триста и сорок», «двести и пять». Предлагается называть число квадратов без использования союза «и»: сто двадцать три, триста сорок и т. д.

Затем предлагаются более сложные упражнения: необходимо назвать число, состоящее из 2 сотен и 5 единиц; 7 сотен и 8 десятков; 9 сотен, 2 десятков и 6 единиц и т. д. По возможности эти упражнения выполняются без использования наглядных пособий.

Одновременно учащимся предлагаются упражнения другого рода. Они отвечают на вопросы: «Сколько сотен, единиц и десятков содержится в числах пятьсот сорок три, двести шестьдесят один, шестьсот два, сто семьдесят?»

Они также должны выполнять разнообразные упражнения.

· Назови по порядку числа от девяносто семи до ста четырех, от ста девяносто девяти до двухсот трех и т. д.

· Назови число, следующее за числом триста девяносто девять; число, меньшее на единицу, чем пятьсот; большее на два, чем восемьсот девяносто девять, и т. д.

· Назови числа, которые находятся между числом триста двадцать шесть и триста тридцать один, и т. д.

· Для работы над этими упражнениями используются модели числового луча — числовая лента, рулетка.

Письменная нумерация трехзначных чисел. Работа над устной нумерацией проводится с опорой на арифметический ящик (его модификации). При изучении письменной нумерации используется позиционный абак. Прежде чем приступить к изучению записи трехзначных чисел, учащиеся учатся изображать на абаке число элементов некоторого множества, и наоборот, определять число элементов множеств по изображению на абаке. В качестве множеств могут использоваться множества квадратов, представленных отдельными квадратами, полосками и пластинками.

Обучение работе с абаком сводится к формированию у учащихся достаточно простого алгоритма. В абаке есть спицы. Крайняя справа предназначена для изображения количества единиц, т. е. отдельных квадратов. На нее нанизывается столько косточек, сколько отдельных квадратов изображено. На вторую спицу нанизываются косточки, которые показывают, сколько полосок (десятков), содер­жит данное число. Наконец на третью спицу — косточки, соответствующие сотням (пластинкам) данного числа. Все эти пояснения следуют по ходу изображения числа (квадратов) на абаке.

Например, на абаке нужно отложить число 567. Для наглядности его можно представить в виде множества квадратов (пластинок, полосок и отдельных квадратов). Затем, в соответствии с числом единиц (квадратов), десятков (полосок), сотен (пластинок), заполняются спицы абака

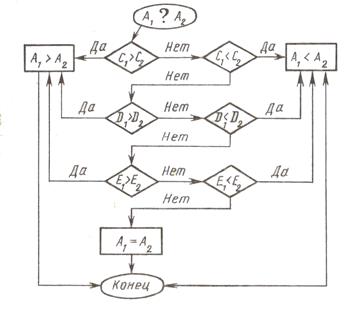
В дальнейшем при выполнении подобных упражнений («Изобразите на абаке число») можно не представлять число в наглядном виде.

Полезны упражнения и другого вида: назвать число, изображенное на абаке. Операции рассмотренного алгоритма выполняются в обратном порядке: сначала подсчитывается количество косточек на спице сотен и называется число сотен в числе, затем — количество косточек на спице десятков и называется число десятков и т. п. Рядом с соответствующими спицами абака записываются цифры.

Учащимся предлагается записывать в тетради цифры, соответствующие показаниям абака, в таком же порядке (слева направо), в каком расположены на абаке спицы сотен, десятков и единиц. Каждую цифру пишут в отдельную клетку тетради. Так появляются записи: 667, 445 и т. д. Трехзначные числа на первых порах читаются с опорой на абак.

Поясним последнее на примере. На доске записывается число 327. Требуется объяснить, что означает эта запись.

Учитель: Что означает цифра 3?

Ученик: Это означает, что на спице сотен три косточки.

Учитель: Что показывают эти косточки?

Ученик: В числе 3 сотни.

Учитель: Что означает цифра 2?

Учитель: Какое же число записано на доске? Ученик: Триста двадцать семь.

С помощью абака рассматривается запись трехзначных чисел особого вида: 200, 209, 290, 400, 470, 407, 500, 505 и т. п. При необходимости снова можно использовать арифметический «ящик».

Например, ставится задача изобразить на абаке и записать число двести. В этом числе 2 сотни, значит, на спице сотен абака откладываются две косточки. Нужно ли откладывать косточки на спице десятков? Очевидно, что нет, так как свободных десятков в числе двести нет. Все они заключены в двух сотнях — двадцать полосок объединены в две пластинки. Такое объяснение позволяет избежать неверной формулировки: «в числе двести нет десятков». Аналогично объясняется отсутствие единиц в разряде единиц числа 200. В соответствии с иллюстрацией на абаке записывается I число 200.

В дальнейшем, когда учащиеся смогут записывать и читать трехзначные числа без опоры на абак, они учатся представлять такие числа в виде суммы разрядных слагаемых.

Из концентра «Сотня» известно, как на языке математики записывается, что число 46, например, состоит из 4 десятков и 6 единиц: 46 = 40 + 6. Этот способ обобщается для трехзначных чисел: число 256 состоит из 2 сотен, 5 десятков и 6 единиц, поэтому 256 = 200 + 50 + 6. Рассматриваются и более сложные случаи: 206 = 200 + 6, 250 = 200 + 50 и т. д. Одновременно изучаются и случаи вычитания, основанные на знании разрядного состава трехзначного числа: 842 - 2 = 840, 842 - 40 = 802, 842 - 800 = 42, 570 - 70 = 500, 570 - 500 = 70, 409 - 9 = 400, 409 - 400 = 9 и т. д.

При выполнении упражнений такого рода учащиеся, с одной стороны, закрепляют знание разрядного состава и поместного значения цифр в трехзначном числе, с другой,— готовятся к изучению операций сложения и вычитания на множестве трехзначных чисел.

Важную роль в изучении нумерации трехзначных чисел играют составные именованные числа, выраженные в мерах длины, стоимости. Использование таких чисел возможно на любом этапе знакомства учащихся с позиционным принципом нумерации. В частности, использование мер длины может помочь учащимся представлять некоторые трехзначные числа в виде двузначных именованных чисел. Такой прием в дальнейшем используется для вычисления значения сумм и разностей определенного вида. Например, чтобы показать, что число 490 содержит 49 десятков и может быть представлено в виде 49 десятков, рассматривается следующая система упражнений: «Сколько дециметров содержится в 4 м и 9 дм? в 490 см? в 590 см?» и т. д.

Сравнение чисел в пределах 1 000 осуществляется аналогично сравнению чисел в пределах 100. Прежде всего необходимо установить, что всякое трехзначное число, даже самое маленькое, больше любого, даже самого большого, двузначного числа (100 > 99). Этим самым сравнение чисел в пределах 1000 сводится к сравнению трехзначных чисел.

На примерах выясняется, что из двух трехзначных чисел то больше, у которого цифра сотен больше (321 > 285, 505 > 396 и т. п.). Если же цифры сотен двух сравниваемых чисел равны, то сравниваются цифры десятков, и то число больше, у которого цифра десятков больше (485 > 478, 315 > 308 и т. п.). Если же и цифры десятков равны, то сравниваются цифры единиц, и то число больше, у которого цифра единиц больше (576 > 572, 105 > 101 и т. п.).

Два трехзначных числа равны тогда и только тогда, когда цифры их одноименных разрядов (сотен, десятков, единиц) равны (одинаковы).

Описанный алгоритм можно представить (для учителя, конечно) в виде схемы.

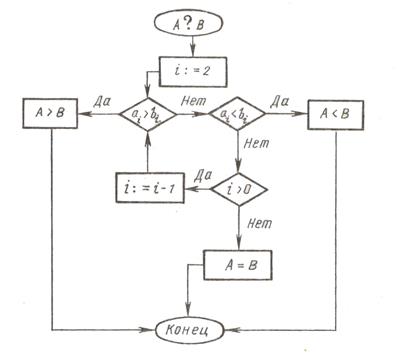
Пусть необходимо сравнить два трёхзначных числа:

цифры сотен, десятков и единиц числа А₂

Однако эта схема алгоритма построена нерационально, хотя по дидактическим соображениям более понятна. Циклический характер процесса сравнения отражается в более простой схеме

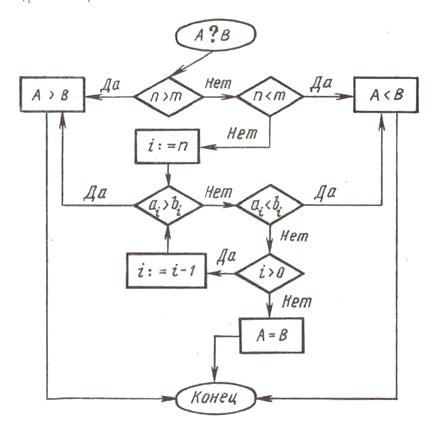
Введем следующие обозначения: А и В — сравниваемые числа

Этот алгоритм легко обобщается для сравнения двух многозначных чисел: А = а_па_п-₁...а₀, B = b_mb_m- ₁ ...b₁b₀