
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Скалярные и векторные величиныСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте Скалярная величина – это физическая величина, которая имеет только одну характеристику – численное значение. Скалярная величина может быть положительной или отрицательной. Примеры скалярных величин: температура, масса, объем, время, плотность. Математические действия со скалярными величинами – это алгебраические действия.
1) численное значение, которое всегда положительно (модуль вектора); 2) направление. Примеры векторных физических величин: скорость, ускорение, сила. Векторная величина обозначается латинской буквой и стрелкой над этой буквой. Например: - вектор скорости обозначается символом - вектор ускорения обозначается символом - вектор силы обозначается символом Модуль вектора обозначается так:
На рисунке (графически) вектор изображается направленным отрезком прямой линии. Модуль вектора равен длине направленного отрезка в заданном масштабе.
Действия с векторами Математические действия с векторными величинами – это геометрические действия. Сравнение векторов Равные векторы. Два вектора равны, если они имеют: - равные модули, - одинаковые направления. Противоположные векторы. Два вектора противоположны, если они имеют: - равные модули, - противоположные направления. - Сложение векторов Мы можем сложить два вектора геометрически по правилу параллелограмма и по правилу треугольника. Пусть заданы два вектора
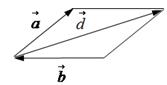
Правило параллелограмма для сложения двух векторов:
2. Нарисуем вектор 3. Через конец вектора 4. Через конец вектора Мы построили параллелограмм. Стороны этого параллелограмма – составляющие векторы 5. Проведем диагональ параллелограмма из общей точки начала вектора 6. Модуль результирующего вектора
начало вектора
Правило треугольника для сложения двух векторов:
1. Нарисуем составляющие векторы 2. Результирующий вектор 3. Модуль результирующего вектора находим по формуле:
Вычитание векторов Вычитание векторов – это действие, обратное сложению:
Найти разность вектора Правило параллелограмма. Стороны параллелограмма - вектор
Правило треугольника. Вектор разности
Умножение вектора на скаляр Пусть заданы вектор В результате умножения вектора на скаляр мы получаем новый вектор Направление вектора Направление вектора Модуль вектора
|
||
|
Последнее изменение этой страницы: 2016-12-27; просмотров: 869; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.007 с.) |

 Векторная величина – это физическая величина, которая имеет две характеристики:
Векторная величина – это физическая величина, которая имеет две характеристики: ,
, ,
, .
. или - модуль вектора
или - модуль вектора  или - модуль вектора
или - модуль вектора 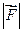 или - модуль вектора
или - модуль вектора 
 (см. рис.). Найдем сумму этих векторов
(см. рис.). Найдем сумму этих векторов  +
+  =
=  . Величины
. Величины  1. Нарисуем вектор
1. Нарисуем вектор  .
. так, что его начало совпадает с началом вектора
так, что его начало совпадает с началом вектора  (см. рисунок).
(см. рисунок). .
. равен длине диагонали параллелограмма и определяется по формуле:
равен длине диагонали параллелограмма и определяется по формуле: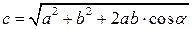 ;
;

 .
. направлен так, что его начало совпадает с началом вектора
направлен так, что его начало совпадает с началом вектора 

 , противоположного вектору
, противоположного вектору  .
.
 соединяет конец вектора
соединяет конец вектора 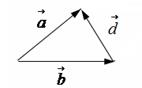
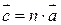
 .
. .
. .
.


