
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Закон сохранения импульса и момента импульсаСодержание книги
Поиск на нашем сайте
При взаимодействии частиц системы между собой полный вектор импульса системы остается постоянным в случаях, когда а) При взаимодействии частиц системы между собой полный вектор момента импульса системы остается постоянным в случаях, когда а) Момент импульса частицы
10-3. Маленький пластилиновый шарик массы m 1 движется горизонтально со скоростью 10-4. Маленький пластилиновый шарик массы m 1 движется горизонтально со скоростью
Литература
1. Савельев И.В. Курс общей физики: учебное пособие для вузов:[в 3 т.]. Т.1. Механика. Молекулярная физика / И.В. Савельев.- 5-е изд. стер. — СПб. и др.: Лань, 2006. - 432 с. 2. Савельев И.В. Сборник вопросов и задач по общей физике: учеб. пособие для втузов / И.В.Савельев.— СПб. и др.: Лань, 2005. - 288 с. 3. Стрелков С.П. Сборник задач по общему курсу физики: в 5 кн. - 5-е изд., стер.— М: Физматлит: Лань, 2006.— (Общий курс физики). Кн. 1: Механика / С. П. Стрелков [и др.]; под ред. И. А. Яковлева. - 2006. - 240 с. 4. Матвеев А.Н. Механика и теория относительности: Учебник для вузов / А.Н.Матвеев.- 3-е изд. - М.: ОНИКС 21 век: Мир и образование, 2003. - 432 с. 5. Трофимова Т.И. Сборник задач по курсу физики с решениями: учеб. пособие для вузов / Т.И.Трофимова.- 8-е изд. перераб. - М.: Высш. шк., 2007. - 591 с. 6. Трофимова Т.И. Основы физики: учеб. пособие:в 5 кн. Кн.1. Механика / Т.И.Трофимова.- М.: Высш. шк., 2007.- 220с 7. Трофимова Т.И. Справочник по физике для студентов и абитуриентов / Т.И.Трофимова.— М.: Астрель:АСТ: Профиздат, 2005. - 399 с. 8. Яворский Б.М. Справочник по физике для инженеров и студентов вузов / Б. М. Яворский, А. А. Детлаф, А. К. Лебедев.- 8-е изд., перераб. и испр. - М.: ОНИКС: Мир и Образование, 2007. - 1055 с. 9. Полянин А.Д. Универсальный справочник. Высшая математика. Физика. Теоретическая механика. Сопротивление материалов / А.Д.Полянин [и др.].- М.: АСТ:Астрель: Профиздат, 2005. - 480 с.
|
||||
|
Последнее изменение этой страницы: 2016-12-27; просмотров: 366; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.119.117.122 (0.008 с.) |

 , б)
, б)  и время взаимодействия очень мало. В этих случаях
и время взаимодействия очень мало. В этих случаях  , где
, где  – векторная сумма импульсов частиц, которые существовали до взаимодействия,
– векторная сумма импульсов частиц, которые существовали до взаимодействия,  – векторная сумма импульсов всех частиц, которые будут существовать после взаимодействия. Если
– векторная сумма импульсов всех частиц, которые будут существовать после взаимодействия. Если  , то сохраняется только проекция полного импульса системы на ось x,
, то сохраняется только проекция полного импульса системы на ось x,  .
. , б)
, б)  и время взаимодействия очень мало. В этих случаях
и время взаимодействия очень мало. В этих случаях  где
где  – векторная сумма моментов импульсов частиц, которые существовали до взаимодействия,
– векторная сумма моментов импульсов частиц, которые существовали до взаимодействия,  – векторная сумма моментов импульсов всех частиц, которые будут существовать после взаимодействия. Если
– векторная сумма моментов импульсов всех частиц, которые будут существовать после взаимодействия. Если  , то сохраняется только проекция момента импульса системы на ось z
, то сохраняется только проекция момента импульса системы на ось z  (часто относительно закрепленной оси вращения).
(часто относительно закрепленной оси вращения). , где
, где  – радиус-вектор частицы,
– радиус-вектор частицы,  – импульс частицы.
– импульс частицы.  , где a – угол между
, где a – угол между  . Для твердого тела, вращающегося вокруг закрепленной оси z
. Для твердого тела, вращающегося вокруг закрепленной оси z  , где
, где  – момент инерции тела относительно оси z,
– момент инерции тела относительно оси z,  – угловая скорость.
– угловая скорость. 10-1. Маленький пластилиновый шарик массы m 1 движется горизонтально со скоростью
10-1. Маленький пластилиновый шарик массы m 1 движется горизонтально со скоростью  . Под углом a к направлению его движения летит второй шарик массы m 2 со скоростью
. Под углом a к направлению его движения летит второй шарик массы m 2 со скоростью  и сталкивается с первым. Шарики слипаются и движутся под углом b к первоначальному направлению движения второго шарика. Найдите
и сталкивается с первым. Шарики слипаются и движутся под углом b к первоначальному направлению движения второго шарика. Найдите  . Если
. Если  1 кг,
1 кг,  2 кг,
2 кг,  1 м/с,
1 м/с,  2 м/с, a = 30°.
2 м/с, a = 30°. . Найдите после удара модуль импульса шариков. Если
. Найдите после удара модуль импульса шариков. Если  и
и  . Если
. Если  10-5. На горизонтальной плоскости лежит тонкий однородный стержень массы m =1 кг и длины l, который может вращаться вокруг вертикальной оси, проходящей через центр масс стержня С. Под углом a =30° к стержню в той же плоскости движется маленький пластилиновый шарик такой же массы m со скоростью
10-5. На горизонтальной плоскости лежит тонкий однородный стержень массы m =1 кг и длины l, который может вращаться вокруг вертикальной оси, проходящей через центр масс стержня С. Под углом a =30° к стержню в той же плоскости движется маленький пластилиновый шарик такой же массы m со скоростью  = 1 м/с. Шарик прилипает к концу стержня, и система приобретает угловую скорость вращения w. Найти угловую скорость вращения системы после удара, если l = 1 м.
= 1 м/с. Шарик прилипает к концу стержня, и система приобретает угловую скорость вращения w. Найти угловую скорость вращения системы после удара, если l = 1 м.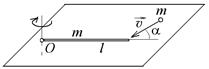 10-6. На горизонтальной плоскости лежит тонкий однородный стержень массы m =1 кг и длины l, который может вращаться вокруг вертикальной оси, проходящей через конец стержня О. Под углом a =30° к стержню в той же плоскости движется маленький пластилиновый шарик такой же массы m со скоростью
10-6. На горизонтальной плоскости лежит тонкий однородный стержень массы m =1 кг и длины l, который может вращаться вокруг вертикальной оси, проходящей через конец стержня О. Под углом a =30° к стержню в той же плоскости движется маленький пластилиновый шарик такой же массы m со скоростью  10-7. Тонкий однородный диск массы m = 1 кг и радиуса R может вращаться в вертикальной плоскости вокруг горизонтальной оси, проходящей через его центр С. Под углом a =30° к вертикали в плоскости вращения диска движется маленький пластилиновый шарик такой же массы m со скоростью
10-7. Тонкий однородный диск массы m = 1 кг и радиуса R может вращаться в вертикальной плоскости вокруг горизонтальной оси, проходящей через его центр С. Под углом a =30° к вертикали в плоскости вращения диска движется маленький пластилиновый шарик такой же массы m со скоростью  10-8. Тонкий однородный стержень массы m = 1 кг и длины l может вращаться в вертикальной плоскости вокруг горизонтальной оси, проходящей через его конец. С разных сторон на стержень горизонтально в той же плоскости налетают два одинаковых пластилиновых шарика той же массы m с одинаковыми скоростями
10-8. Тонкий однородный стержень массы m = 1 кг и длины l может вращаться в вертикальной плоскости вокруг горизонтальной оси, проходящей через его конец. С разных сторон на стержень горизонтально в той же плоскости налетают два одинаковых пластилиновых шарика той же массы m с одинаковыми скоростями  10-9. Тонкий однородный стержень массы m =1 кг и длины l может вращаться в вертикальной плоскости вокруг горизонтальной оси, проходящей через его конец O. Горизонтально в той же плоскости на стержень налетает пластилиновый шарик той же массы m со скоростью
10-9. Тонкий однородный стержень массы m =1 кг и длины l может вращаться в вертикальной плоскости вокруг горизонтальной оси, проходящей через его конец O. Горизонтально в той же плоскости на стержень налетает пластилиновый шарик той же массы m со скоростью  от точки О, и система приобретает угловую скорость w. Найти угловую скорость вращения системы после удара, если l = 1 м.
от точки О, и система приобретает угловую скорость w. Найти угловую скорость вращения системы после удара, если l = 1 м.
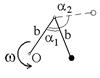 10-10. Два невесомых стержня длины b соединены под углом a1 = 60° и вращаются без трения в горизонтальной плоскости вокруг вертикальной оси О с угловой скоростью w = 2 рад/с. На конце одного из стержней прикреплен очень маленький массивный шарик. В некоторый момент угол между стержнями самопроизвольно увеличился до a2 = 120°. С какой угловой скоростью стала вращаться такая система?
10-10. Два невесомых стержня длины b соединены под углом a1 = 60° и вращаются без трения в горизонтальной плоскости вокруг вертикальной оси О с угловой скоростью w = 2 рад/с. На конце одного из стержней прикреплен очень маленький массивный шарик. В некоторый момент угол между стержнями самопроизвольно увеличился до a2 = 120°. С какой угловой скоростью стала вращаться такая система?


